Voronoi Candidates for Bayesian Optimization

Bayesian optimization (BO) offers an elegant approach for efficiently optimizing black-box functions. However, acquisition criteria demand their own challenging inner-optimization, which can induce significant overhead. Many practical BO methods, particularly in high dimension, eschew a formal, continuous optimization of the acquisition function and instead search discretely over a finite set of space-filling candidates. Here, we propose to use candidates which lie on the boundary of the Voronoi tessellation of the current design points, so they are equidistant to two or more of them. We discuss strategies for efficient implementation by directly sampling the Voronoi boundary without explicitly generating the tessellation, thus accommodating large designs in high dimension. On a battery of test problems optimized via Gaussian processes with expected improvement, our proposed approach significantly improves the execution time of a multi-start continuous search without a loss in accuracy.

Robust expected improvement for Bayesian optimization

Bayesian Optimization (BO) links Gaussian Process (GP) surrogates with sequential design toward optimizing expensive-to-evaluate black-box functions. Example design heuristics, or so-called acquisition functions, like expected improvement (EI), balance exploration and exploitation to furnish global solutions under stringent evaluation budgets. However, they fall short when solving for robust optima, meaning a preference for solutions in a wider domain of attraction. Robust solutions are useful when inputs are imprecisely specified, or where a series of solutions is desired. A common mathematical programming technique in such settings involves an adversarial objective, biasing a local solver away from ``sharp'' troughs. Here we propose a surrogate modeling and active learning technique called robust expected improvement (REI) that ports adversarial methodology into the BO/GP framework. After describing the methods, we illustrate and draw comparisons to several competitors on benchmark synthetic and real problems of varying complexity.

Triangulation candidates for Bayesian optimization

Bayesian optimization is a form of sequential design: idealize input-output relationships with a suitably flexible nonlinear regression model; fit to data from an initial experimental campaign; devise and optimize a criterion for selecting the next experimental condition(s) under the fitted model (e.g., via predictive equations) to target outcomes of interest (say minima); repeat after acquiring output under those conditions and updating the fit. In many situations this "inner optimization" over the new-data acquisition criterion is cumbersome because it is non-convex/highly multi-modal, may be non-differentiable, or may otherwise thwart numerical optimizers, especially when inference requires Monte Carlo. In such cases it is not uncommon to replace continuous search with a discrete one over random candidates. Here we propose using candidates based on a Delaunay triangulation of the existing input design. In addition to detailing construction of these "tricands", based on a simple wrapper around a conventional convex hull library, we promote several advantages based on properties of the geometric criterion involved. We then demonstrate empirically how tricands can lead to better Bayesian optimization performance compared to both numerically optimized acquisitions and random candidate-based alternatives on benchmark problems.

Entropy-based adaptive design for contour finding and estimating reliability

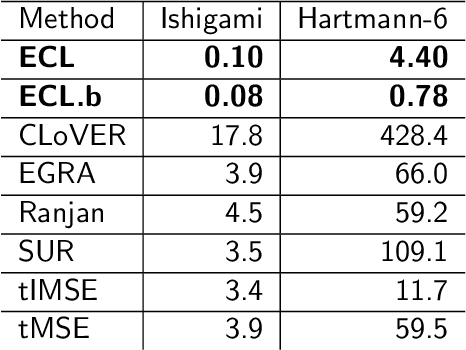
In reliability analysis, methods used to estimate failure probability are often limited by the costs associated with model evaluations. Many of these methods, such as multifidelity importance sampling (MFIS), rely upon a computationally efficient, surrogate model like a Gaussian process (GP) to quickly generate predictions. The quality of the GP fit, particularly in the vicinity of the failure region(s), is instrumental in supplying accurately predicted failures for such strategies. We introduce an entropy-based GP adaptive design that, when paired with MFIS, provides more accurate failure probability estimates and with higher confidence. We show that our greedy data acquisition strategy better identifies multiple failure regions compared to existing contour-finding schemes. We then extend the method to batch selection, without sacrificing accuracy. Illustrative examples are provided on benchmark data as well as an application to an impact damage simulator for National Aeronautics and Space Administration (NASA) spacesuits.

Sensitivity Prewarping for Local Surrogate Modeling

In the continual effort to improve product quality and decrease operations costs, computational modeling is increasingly being deployed to determine feasibility of product designs or configurations. Surrogate modeling of these computer experiments via local models, which induce sparsity by only considering short range interactions, can tackle huge analyses of complicated input-output relationships. However, narrowing focus to local scale means that global trends must be re-learned over and over again. In this article, we propose a framework for incorporating information from a global sensitivity analysis into the surrogate model as an input rotation and rescaling preprocessing step. We discuss the relationship between several sensitivity analysis methods based on kernel regression before describing how they give rise to a transformation of the input variables. Specifically, we perform an input warping such that the "warped simulator" is equally sensitive to all input directions, freeing local models to focus on local dynamics. Numerical experiments on observational data and benchmark test functions, including a high-dimensional computer simulator from the automotive industry, provide empirical validation.

Active Learning for Deep Gaussian Process Surrogates

Deep Gaussian processes (DGPs) are increasingly popular as predictive models in machine learning (ML) for their non-stationary flexibility and ability to cope with abrupt regime changes in training data. Here we explore DGPs as surrogates for computer simulation experiments whose response surfaces exhibit similar characteristics. In particular, we transport a DGP's automatic warping of the input space and full uncertainty quantification (UQ), via a novel elliptical slice sampling (ESS) Bayesian posterior inferential scheme, through to active learning (AL) strategies that distribute runs non-uniformly in the input space -- something an ordinary (stationary) GP could not do. Building up the design sequentially in this way allows smaller training sets, limiting both expensive evaluation of the simulator code and mitigating cubic costs of DGP inference. When training data sizes are kept small through careful acquisition, and with parsimonious layout of latent layers, the framework can be both effective and computationally tractable. Our methods are illustrated on simulation data and two real computer experiments of varying input dimensionality. We provide an open source implementation in the "deepgp" package on CRAN.

Locally induced Gaussian processes for large-scale simulation experiments

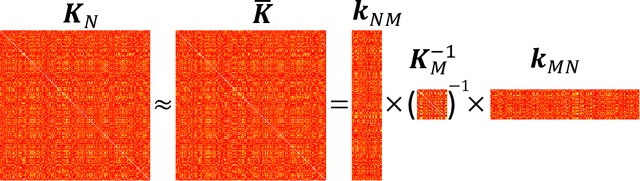
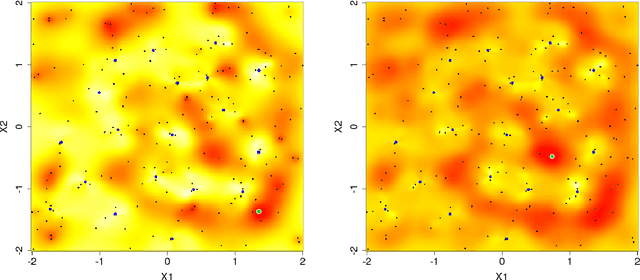
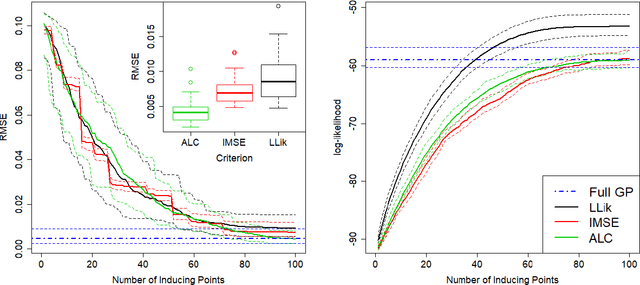
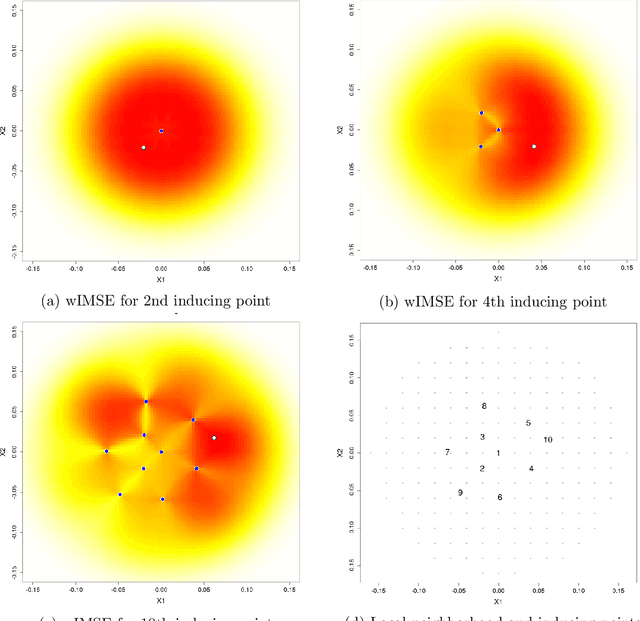
Gaussian processes (GPs) serve as flexible surrogates for complex surfaces, but buckle under the cubic cost of matrix decompositions with big training data sizes. Geospatial and machine learning communities suggest pseudo-inputs, or inducing points, as one strategy to obtain an approximation easing that computational burden. However, we show how placement of inducing points and their multitude can be thwarted by pathologies, especially in large-scale dynamic response surface modeling tasks. As remedy, we suggest porting the inducing point idea, which is usually applied globally, over to a more local context where selection is both easier and faster. In this way, our proposed methodology hybridizes global inducing point and data subset-based local GP approximation. A cascade of strategies for planning the selection of local inducing points is provided, and comparisons are drawn to related methodology with emphasis on computer surrogate modeling applications. We show that local inducing points extend their global and data-subset component parts on the accuracy--computational efficiency frontier. Illustrative examples are provided on benchmark data and a large-scale real-simulation satellite drag interpolation problem.

Bayesian optimization under mixed constraints with a slack-variable augmented Lagrangian

An augmented Lagrangian (AL) can convert a constrained optimization problem into a sequence of simpler (e.g., unconstrained) problems, which are then usually solved with local solvers. Recently, surrogate-based Bayesian optimization (BO) sub-solvers have been successfully deployed in the AL framework for a more global search in the presence of inequality constraints; however, a drawback was that expected improvement (EI) evaluations relied on Monte Carlo. Here we introduce an alternative slack variable AL, and show that in this formulation the EI may be evaluated with library routines. The slack variables furthermore facilitate equality as well as inequality constraints, and mixtures thereof. We show how our new slack "ALBO" compares favorably to the original. Its superiority over conventional alternatives is reinforced on several mixed constraint examples.

Gaussian Process Structural Equation Models with Latent Variables

In a variety of disciplines such as social sciences, psychology, medicine and economics, the recorded data are considered to be noisy measurements of latent variables connected by some causal structure. This corresponds to a family of graphical models known as the structural equation model with latent variables. While linear non-Gaussian variants have been well-studied, inference in nonparametric structural equation models is still underdeveloped. We introduce a sparse Gaussian process parameterization that defines a non-linear structure connecting latent variables, unlike common formulations of Gaussian process latent variable models. The sparse parameterization is given a full Bayesian treatment without compromising Markov chain Monte Carlo efficiency. We compare the stability of the sampling procedure and the predictive ability of the model against the current practice.

Sequential Design for Optimal Stopping Problems

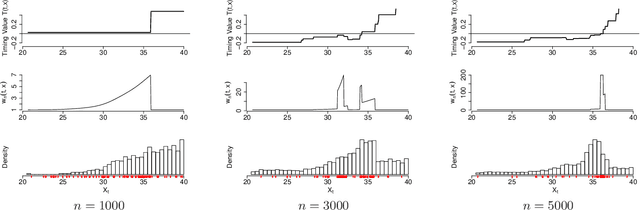
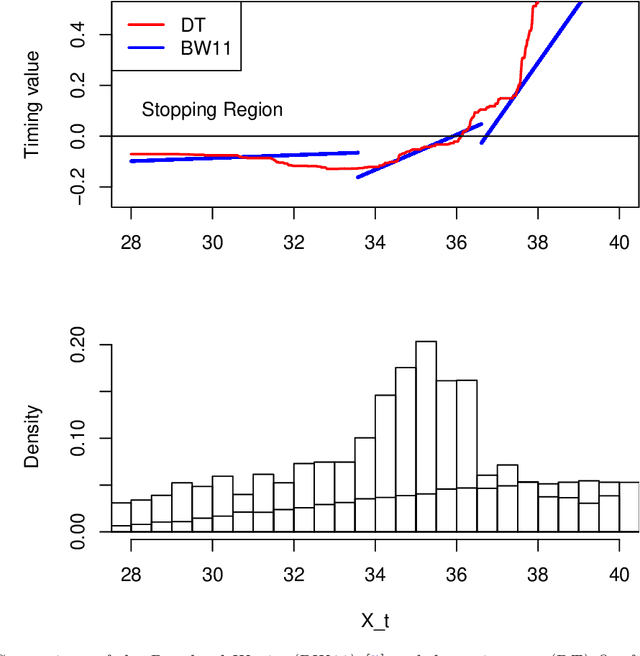
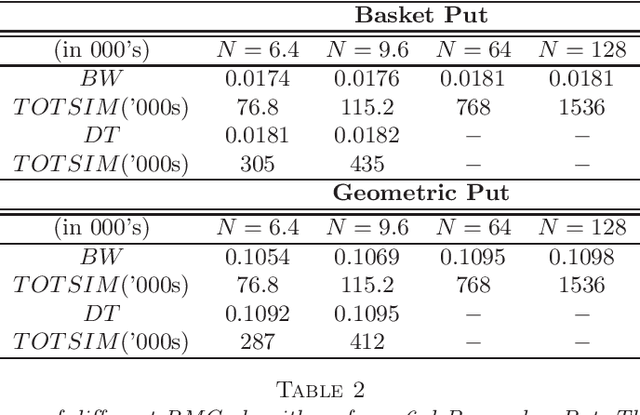
We propose a new approach to solve optimal stopping problems via simulation. Working within the backward dynamic programming/Snell envelope framework, we augment the methodology of Longstaff-Schwartz that focuses on approximating the stopping strategy. Namely, we introduce adaptive generation of the stochastic grids anchoring the simulated sample paths of the underlying state process. This allows for active learning of the classifiers partitioning the state space into the continuation and stopping regions. To this end, we examine sequential design schemes that adaptively place new design points close to the stopping boundaries. We then discuss dynamic regression algorithms that can implement such recursive estimation and local refinement of the classifiers. The new algorithm is illustrated with a variety of numerical experiments, showing that an order of magnitude savings in terms of design size can be achieved. We also compare with existing benchmarks in the context of pricing multi-dimensional Bermudan options.