Sequential Design for Optimal Stopping Problems
Paper and Code
Jul 29, 2014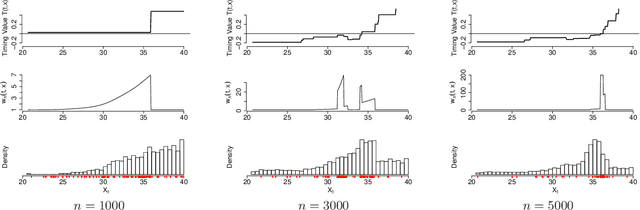

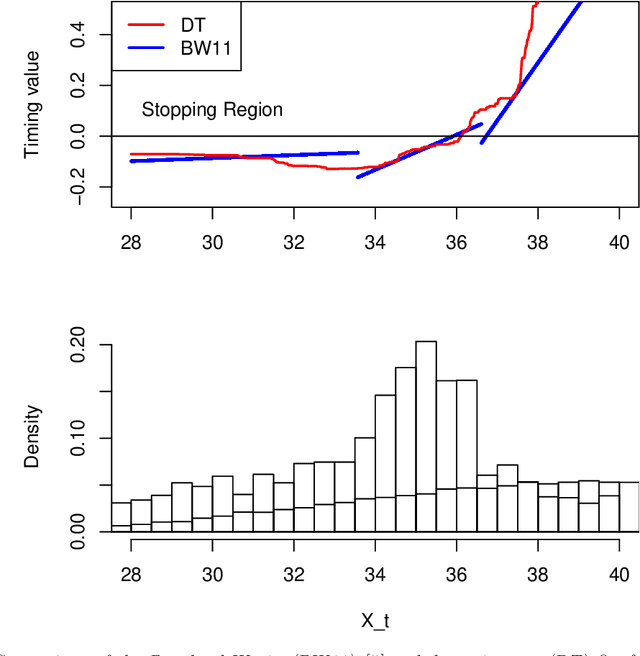
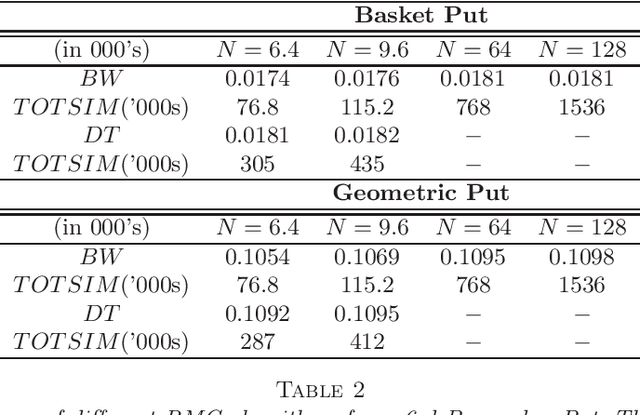
We propose a new approach to solve optimal stopping problems via simulation. Working within the backward dynamic programming/Snell envelope framework, we augment the methodology of Longstaff-Schwartz that focuses on approximating the stopping strategy. Namely, we introduce adaptive generation of the stochastic grids anchoring the simulated sample paths of the underlying state process. This allows for active learning of the classifiers partitioning the state space into the continuation and stopping regions. To this end, we examine sequential design schemes that adaptively place new design points close to the stopping boundaries. We then discuss dynamic regression algorithms that can implement such recursive estimation and local refinement of the classifiers. The new algorithm is illustrated with a variety of numerical experiments, showing that an order of magnitude savings in terms of design size can be achieved. We also compare with existing benchmarks in the context of pricing multi-dimensional Bermudan options.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge