Entropy-based adaptive design for contour finding and estimating reliability

In reliability analysis, methods used to estimate failure probability are often limited by the costs associated with model evaluations. Many of these methods, such as multifidelity importance sampling (MFIS), rely upon a computationally efficient, surrogate model like a Gaussian process (GP) to quickly generate predictions. The quality of the GP fit, particularly in the vicinity of the failure region(s), is instrumental in supplying accurately predicted failures for such strategies. We introduce an entropy-based GP adaptive design that, when paired with MFIS, provides more accurate failure probability estimates and with higher confidence. We show that our greedy data acquisition strategy better identifies multiple failure regions compared to existing contour-finding schemes. We then extend the method to batch selection, without sacrificing accuracy. Illustrative examples are provided on benchmark data as well as an application to an impact damage simulator for National Aeronautics and Space Administration (NASA) spacesuits.

Locally induced Gaussian processes for large-scale simulation experiments

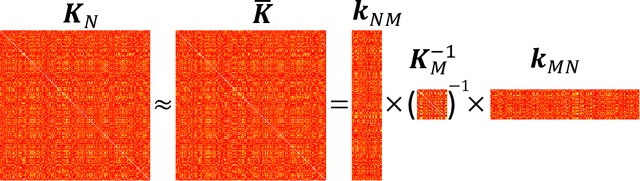
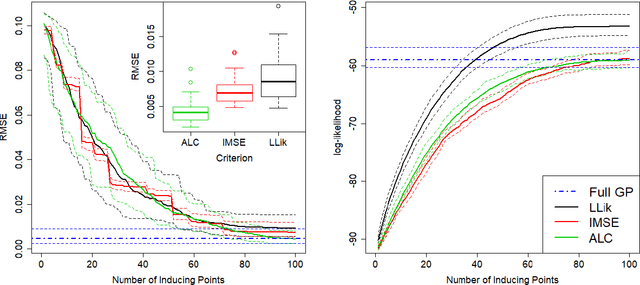
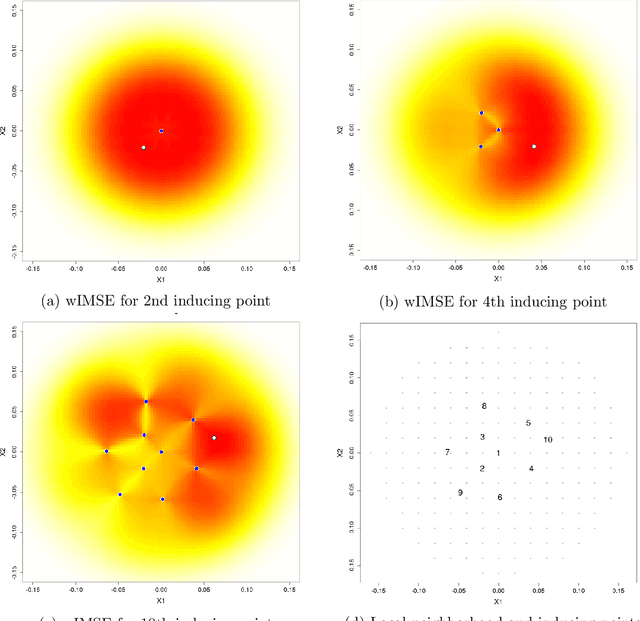
Gaussian processes (GPs) serve as flexible surrogates for complex surfaces, but buckle under the cubic cost of matrix decompositions with big training data sizes. Geospatial and machine learning communities suggest pseudo-inputs, or inducing points, as one strategy to obtain an approximation easing that computational burden. However, we show how placement of inducing points and their multitude can be thwarted by pathologies, especially in large-scale dynamic response surface modeling tasks. As remedy, we suggest porting the inducing point idea, which is usually applied globally, over to a more local context where selection is both easier and faster. In this way, our proposed methodology hybridizes global inducing point and data subset-based local GP approximation. A cascade of strategies for planning the selection of local inducing points is provided, and comparisons are drawn to related methodology with emphasis on computer surrogate modeling applications. We show that local inducing points extend their global and data-subset component parts on the accuracy--computational efficiency frontier. Illustrative examples are provided on benchmark data and a large-scale real-simulation satellite drag interpolation problem.