Formal Bayesian Transfer Learning via the Total Risk Prior

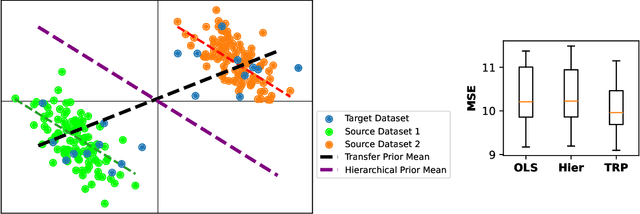
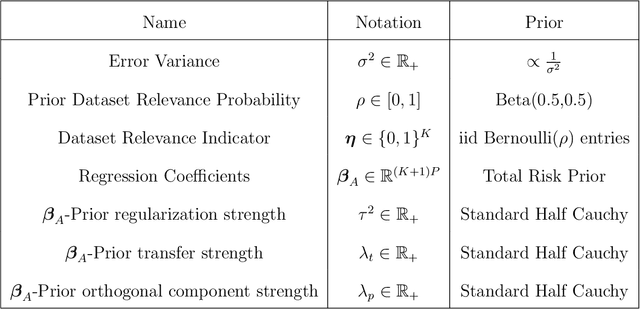
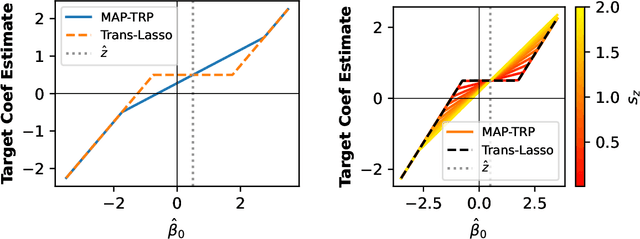
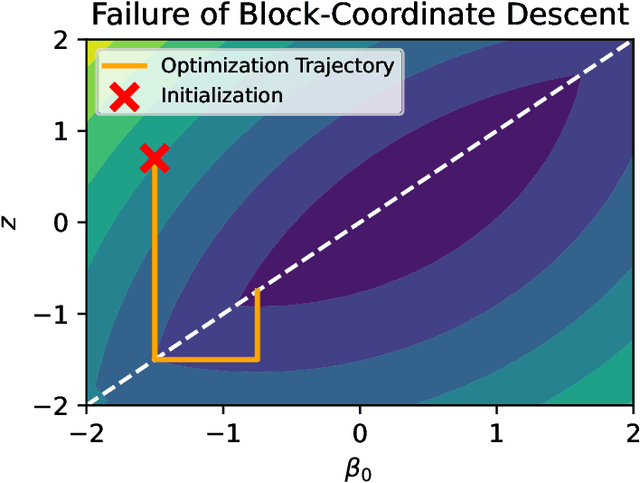
In analyses with severe data-limitations, augmenting the target dataset with information from ancillary datasets in the application domain, called source datasets, can lead to significantly improved statistical procedures. However, existing methods for this transfer learning struggle to deal with situations where the source datasets are also limited and not guaranteed to be well-aligned with the target dataset. A typical strategy is to use the empirical loss minimizer on the source data as a prior mean for the target parameters, which places the estimation of source parameters outside of the Bayesian formalism. Our key conceptual contribution is to use a risk minimizer conditional on source parameters instead. This allows us to construct a single joint prior distribution for all parameters from the source datasets as well as the target dataset. As a consequence, we benefit from full Bayesian uncertainty quantification and can perform model averaging via Gibbs sampling over indicator variables governing the inclusion of each source dataset. We show how a particular instantiation of our prior leads to a Bayesian Lasso in a transformed coordinate system and discuss computational techniques to scale our approach to moderately sized datasets. We also demonstrate that recently proposed minimax-frequentist transfer learning techniques may be viewed as an approximate Maximum a Posteriori approach to our model. Finally, we demonstrate superior predictive performance relative to the frequentist baseline on a genetics application, especially when the source data are limited.

Proximal Iteration for Nonlinear Adaptive Lasso

Augmenting a smooth cost function with an $\ell_1$ penalty allows analysts to efficiently conduct estimation and variable selection simultaneously in sophisticated models and can be efficiently implemented using proximal gradient methods. However, one drawback of the $\ell_1$ penalty is bias: nonzero parameters are underestimated in magnitude, motivating techniques such as the Adaptive Lasso which endow each parameter with its own penalty coefficient. But it's not clear how these parameter-specific penalties should be set in complex models. In this article, we study the approach of treating the penalty coefficients as additional decision variables to be learned in a \textit{Maximum a Posteriori} manner, developing a proximal gradient approach to joint optimization of these together with the parameters of any differentiable cost function. Beyond reducing bias in estimates, this procedure can also encourage arbitrary sparsity structure via a prior on the penalty coefficients. We compare our method to implementations of specific sparsity structures for non-Gaussian regression on synthetic and real datasets, finding our more general method to be competitive in terms of both speed and accuracy. We then consider nonlinear models for two case studies: COVID-19 vaccination behavior and international refugee movement, highlighting the applicability of this approach to complex problems and intricate sparsity structures.

Regression Trees Know Calculus

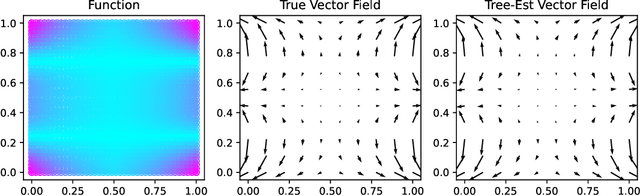
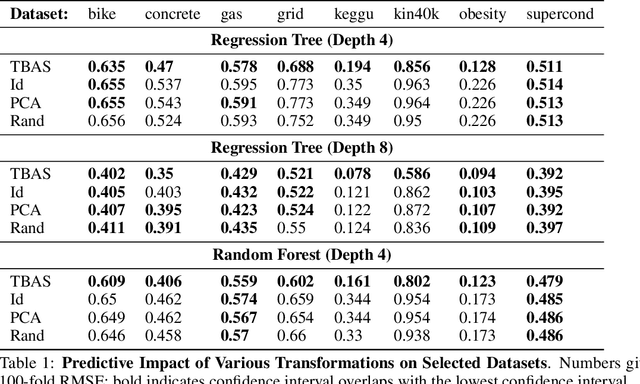
Regression trees have emerged as a preeminent tool for solving real-world regression problems due to their ability to deal with nonlinearities, interaction effects and sharp discontinuities. In this article, we rather study regression trees applied to well-behaved, differentiable functions, and determine the relationship between node parameters and the local gradient of the function being approximated. We find a simple estimate of the gradient which can be efficiently computed using quantities exposed by popular tree learning libraries. This allows the tools developed in the context of differentiable algorithms, like neural nets and Gaussian processes, to be deployed to tree-based models. To demonstrate this, we study measures of model sensitivity defined in terms of integrals of gradients and demonstrate how to compute them for regression trees using the proposed gradient estimates. Quantitative and qualitative numerical experiments reveal the capability of gradients estimated by regression trees to improve predictive analysis, solve tasks in uncertainty quantification, and provide interpretation of model behavior.

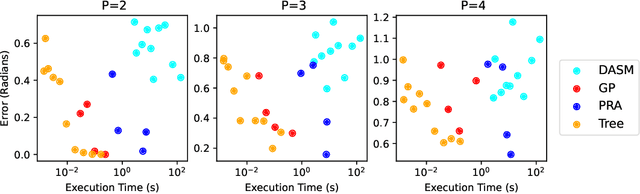
Voronoi Candidates for Bayesian Optimization

Bayesian optimization (BO) offers an elegant approach for efficiently optimizing black-box functions. However, acquisition criteria demand their own challenging inner-optimization, which can induce significant overhead. Many practical BO methods, particularly in high dimension, eschew a formal, continuous optimization of the acquisition function and instead search discretely over a finite set of space-filling candidates. Here, we propose to use candidates which lie on the boundary of the Voronoi tessellation of the current design points, so they are equidistant to two or more of them. We discuss strategies for efficient implementation by directly sampling the Voronoi boundary without explicitly generating the tessellation, thus accommodating large designs in high dimension. On a battery of test problems optimized via Gaussian processes with expected improvement, our proposed approach significantly improves the execution time of a multi-start continuous search without a loss in accuracy.

Surrogate Active Subspaces for Jump-Discontinuous Functions

Surrogate modeling and active subspaces have emerged as powerful paradigms in computational science and engineering. Porting such techniques to computational models in the social sciences brings into sharp relief their limitations in dealing with discontinuous simulators, such as Agent-Based Models, which have discrete outputs. Nevertheless, prior applied work has shown that surrogate estimates of active subspaces for such estimators can yield interesting results. But given that active subspaces are defined by way of gradients, it is not clear what quantity is being estimated when this methodology is applied to a discontinuous simulator. We begin this article by showing some pathologies that can arise when conducting such an analysis. This motivates an extension of active subspaces to discontinuous functions, clarifying what is actually being estimated in such analyses. We also conduct numerical experiments on synthetic test functions to compare Gaussian process estimates of active subspaces on continuous and discontinuous functions. Finally, we deploy our methodology on Flee, an agent-based model of refugee movement, yielding novel insights into which parameters of the simulation are most important across 8 displacement crises in Africa and the Middle East.

Sparse Bayesian Lasso via a Variable-Coefficient $\ell_1$ Penalty

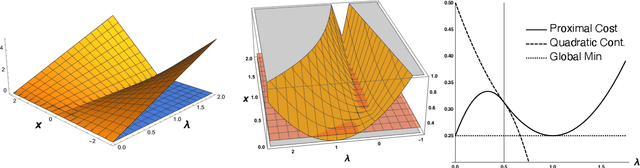
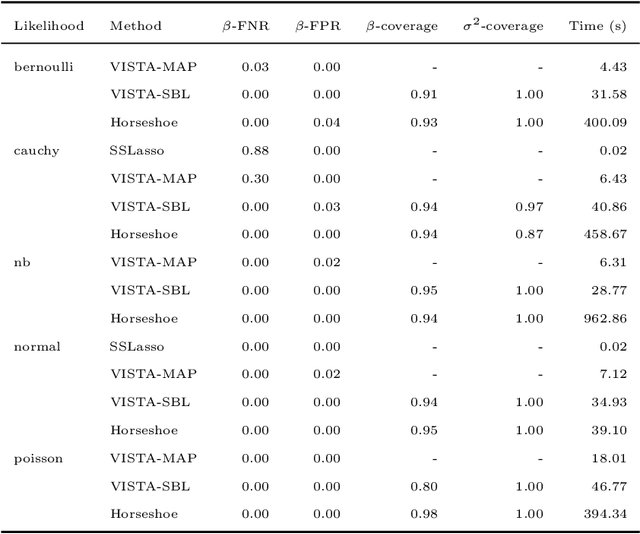
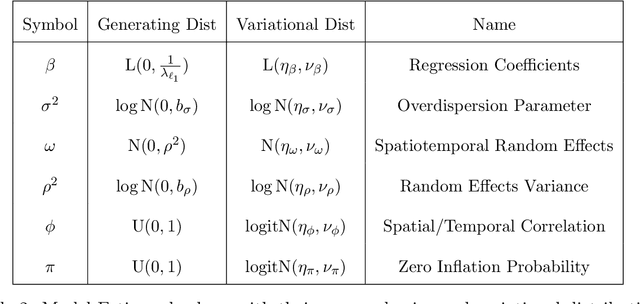
Modern statistical learning algorithms are capable of amazing flexibility, but struggle with interpretability. One possible solution is sparsity: making inference such that many of the parameters are estimated as being identically 0, which may be imposed through the use of nonsmooth penalties such as the $\ell_1$ penalty. However, the $\ell_1$ penalty introduces significant bias when high sparsity is desired. In this article, we retain the $\ell_1$ penalty, but define learnable penalty weights $\lambda_p$ endowed with hyperpriors. We start the article by investigating the optimization problem this poses, developing a proximal operator associated with the $\ell_1$ norm. We then study the theoretical properties of this variable-coefficient $\ell_1$ penalty in the context of penalized likelihood. Next, we investigate application of this penalty to Variational Bayes, developing a model we call the Sparse Bayesian Lasso which allows for behavior qualitatively like Lasso regression to be applied to arbitrary variational models. In simulation studies, this gives us the Uncertainty Quantification and low bias properties of simulation-based approaches with an order of magnitude less computation. Finally, we apply our methodology to a Bayesian lagged spatiotemporal regression model of internal displacement that occurred during the Iraqi Civil War of 2013-2017.

Triangulation candidates for Bayesian optimization

Bayesian optimization is a form of sequential design: idealize input-output relationships with a suitably flexible nonlinear regression model; fit to data from an initial experimental campaign; devise and optimize a criterion for selecting the next experimental condition(s) under the fitted model (e.g., via predictive equations) to target outcomes of interest (say minima); repeat after acquiring output under those conditions and updating the fit. In many situations this "inner optimization" over the new-data acquisition criterion is cumbersome because it is non-convex/highly multi-modal, may be non-differentiable, or may otherwise thwart numerical optimizers, especially when inference requires Monte Carlo. In such cases it is not uncommon to replace continuous search with a discrete one over random candidates. Here we propose using candidates based on a Delaunay triangulation of the existing input design. In addition to detailing construction of these "tricands", based on a simple wrapper around a conventional convex hull library, we promote several advantages based on properties of the geometric criterion involved. We then demonstrate empirically how tricands can lead to better Bayesian optimization performance compared to both numerically optimized acquisitions and random candidate-based alternatives on benchmark problems.

Neko: a Library for Exploring Neuromorphic Learning Rules

The field of neuromorphic computing is in a period of active exploration. While many tools have been developed to simulate neuronal dynamics or convert deep networks to spiking models, general software libraries for learning rules remain underexplored. This is partly due to the diverse, challenging nature of efforts to design new learning rules, which range from encoding methods to gradient approximations, from population approaches that mimic the Bayesian brain to constrained learning algorithms deployed on memristor crossbars. To address this gap, we present Neko, a modular, extensible library with a focus on aiding the design of new learning algorithms. We demonstrate the utility of Neko in three exemplar cases: online local learning, probabilistic learning, and analog on-device learning. Our results show that Neko can replicate the state-of-the-art algorithms and, in one case, lead to significant outperformance in accuracy and speed. Further, it offers tools including gradient comparison that can help develop new algorithmic variants. Neko is an open source Python library that supports PyTorch and TensorFlow backends.

Sensitivity Prewarping for Local Surrogate Modeling

In the continual effort to improve product quality and decrease operations costs, computational modeling is increasingly being deployed to determine feasibility of product designs or configurations. Surrogate modeling of these computer experiments via local models, which induce sparsity by only considering short range interactions, can tackle huge analyses of complicated input-output relationships. However, narrowing focus to local scale means that global trends must be re-learned over and over again. In this article, we propose a framework for incorporating information from a global sensitivity analysis into the surrogate model as an input rotation and rescaling preprocessing step. We discuss the relationship between several sensitivity analysis methods based on kernel regression before describing how they give rise to a transformation of the input variables. Specifically, we perform an input warping such that the "warped simulator" is equally sensitive to all input directions, freeing local models to focus on local dynamics. Numerical experiments on observational data and benchmark test functions, including a high-dimensional computer simulator from the automotive industry, provide empirical validation.

Towards On-Chip Bayesian Neuromorphic Learning

If edge devices are to be deployed to critical applications where their decisions could have serious financial, political, or public-health consequences, they will need a way to signal when they are not sure how to react to their environment. For instance, a lost delivery drone could make its way back to a distribution center or contact the client if it is confused about how exactly to make its delivery, rather than taking the action which is "most likely" correct. This issue is compounded for health care or military applications. However, the brain-realistic temporal credit assignment problem neuromorphic computing algorithms have to solve is difficult. The double role weights play in backpropagation-based-learning, dictating how the network reacts to both input and feedback, needs to be decoupled. e-prop 1 is a promising learning algorithm that tackles this with Broadcast Alignment (a technique where network weights are replaced with random weights during feedback) and accumulated local information. We investigate under what conditions the Bayesian loss term can be expressed in a similar fashion, proposing an algorithm that can be computed with only local information as well and which is thus no more difficult to implement on hardware. This algorithm is exhibited on a store-recall problem, which suggests that it can learn good uncertainty on decisions to be made over time.