Proximal Iteration for Nonlinear Adaptive Lasso

Augmenting a smooth cost function with an $\ell_1$ penalty allows analysts to efficiently conduct estimation and variable selection simultaneously in sophisticated models and can be efficiently implemented using proximal gradient methods. However, one drawback of the $\ell_1$ penalty is bias: nonzero parameters are underestimated in magnitude, motivating techniques such as the Adaptive Lasso which endow each parameter with its own penalty coefficient. But it's not clear how these parameter-specific penalties should be set in complex models. In this article, we study the approach of treating the penalty coefficients as additional decision variables to be learned in a \textit{Maximum a Posteriori} manner, developing a proximal gradient approach to joint optimization of these together with the parameters of any differentiable cost function. Beyond reducing bias in estimates, this procedure can also encourage arbitrary sparsity structure via a prior on the penalty coefficients. We compare our method to implementations of specific sparsity structures for non-Gaussian regression on synthetic and real datasets, finding our more general method to be competitive in terms of both speed and accuracy. We then consider nonlinear models for two case studies: COVID-19 vaccination behavior and international refugee movement, highlighting the applicability of this approach to complex problems and intricate sparsity structures.

Sparse Bayesian Lasso via a Variable-Coefficient $\ell_1$ Penalty

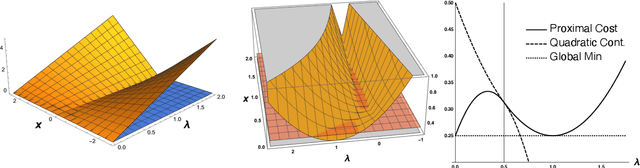
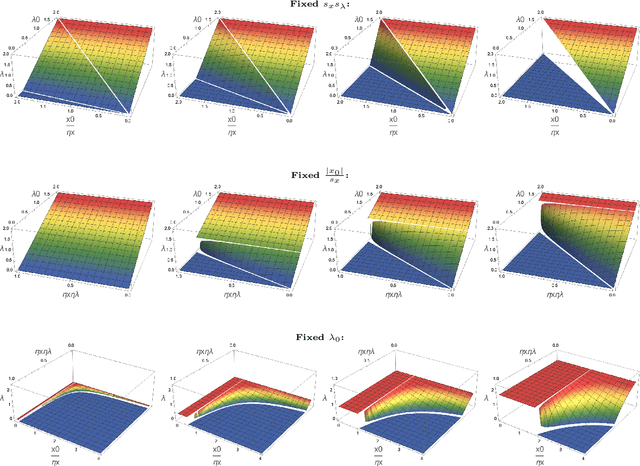
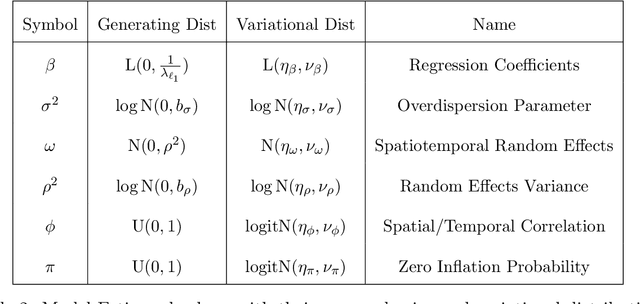
Modern statistical learning algorithms are capable of amazing flexibility, but struggle with interpretability. One possible solution is sparsity: making inference such that many of the parameters are estimated as being identically 0, which may be imposed through the use of nonsmooth penalties such as the $\ell_1$ penalty. However, the $\ell_1$ penalty introduces significant bias when high sparsity is desired. In this article, we retain the $\ell_1$ penalty, but define learnable penalty weights $\lambda_p$ endowed with hyperpriors. We start the article by investigating the optimization problem this poses, developing a proximal operator associated with the $\ell_1$ norm. We then study the theoretical properties of this variable-coefficient $\ell_1$ penalty in the context of penalized likelihood. Next, we investigate application of this penalty to Variational Bayes, developing a model we call the Sparse Bayesian Lasso which allows for behavior qualitatively like Lasso regression to be applied to arbitrary variational models. In simulation studies, this gives us the Uncertainty Quantification and low bias properties of simulation-based approaches with an order of magnitude less computation. Finally, we apply our methodology to a Bayesian lagged spatiotemporal regression model of internal displacement that occurred during the Iraqi Civil War of 2013-2017.