Formal Bayesian Transfer Learning via the Total Risk Prior

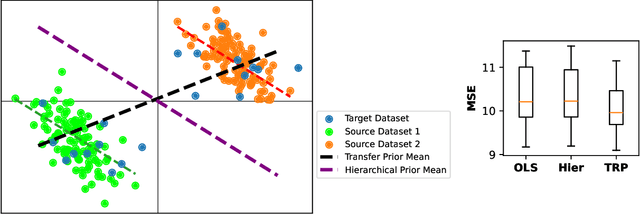
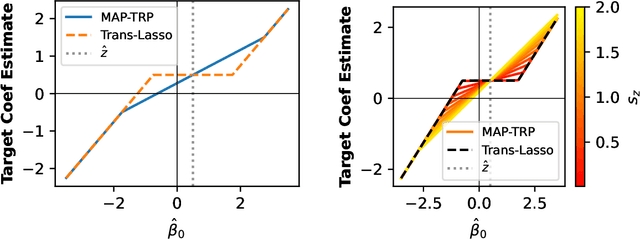
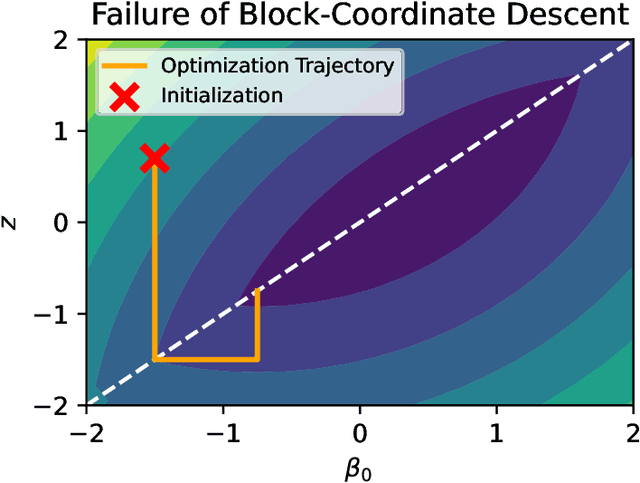
In analyses with severe data-limitations, augmenting the target dataset with information from ancillary datasets in the application domain, called source datasets, can lead to significantly improved statistical procedures. However, existing methods for this transfer learning struggle to deal with situations where the source datasets are also limited and not guaranteed to be well-aligned with the target dataset. A typical strategy is to use the empirical loss minimizer on the source data as a prior mean for the target parameters, which places the estimation of source parameters outside of the Bayesian formalism. Our key conceptual contribution is to use a risk minimizer conditional on source parameters instead. This allows us to construct a single joint prior distribution for all parameters from the source datasets as well as the target dataset. As a consequence, we benefit from full Bayesian uncertainty quantification and can perform model averaging via Gibbs sampling over indicator variables governing the inclusion of each source dataset. We show how a particular instantiation of our prior leads to a Bayesian Lasso in a transformed coordinate system and discuss computational techniques to scale our approach to moderately sized datasets. We also demonstrate that recently proposed minimax-frequentist transfer learning techniques may be viewed as an approximate Maximum a Posteriori approach to our model. Finally, we demonstrate superior predictive performance relative to the frequentist baseline on a genetics application, especially when the source data are limited.

Proximal Iteration for Nonlinear Adaptive Lasso

Augmenting a smooth cost function with an $\ell_1$ penalty allows analysts to efficiently conduct estimation and variable selection simultaneously in sophisticated models and can be efficiently implemented using proximal gradient methods. However, one drawback of the $\ell_1$ penalty is bias: nonzero parameters are underestimated in magnitude, motivating techniques such as the Adaptive Lasso which endow each parameter with its own penalty coefficient. But it's not clear how these parameter-specific penalties should be set in complex models. In this article, we study the approach of treating the penalty coefficients as additional decision variables to be learned in a \textit{Maximum a Posteriori} manner, developing a proximal gradient approach to joint optimization of these together with the parameters of any differentiable cost function. Beyond reducing bias in estimates, this procedure can also encourage arbitrary sparsity structure via a prior on the penalty coefficients. We compare our method to implementations of specific sparsity structures for non-Gaussian regression on synthetic and real datasets, finding our more general method to be competitive in terms of both speed and accuracy. We then consider nonlinear models for two case studies: COVID-19 vaccination behavior and international refugee movement, highlighting the applicability of this approach to complex problems and intricate sparsity structures.

Sparse Bayesian Lasso via a Variable-Coefficient $\ell_1$ Penalty

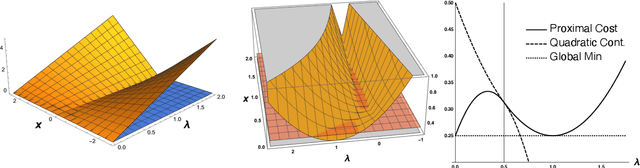
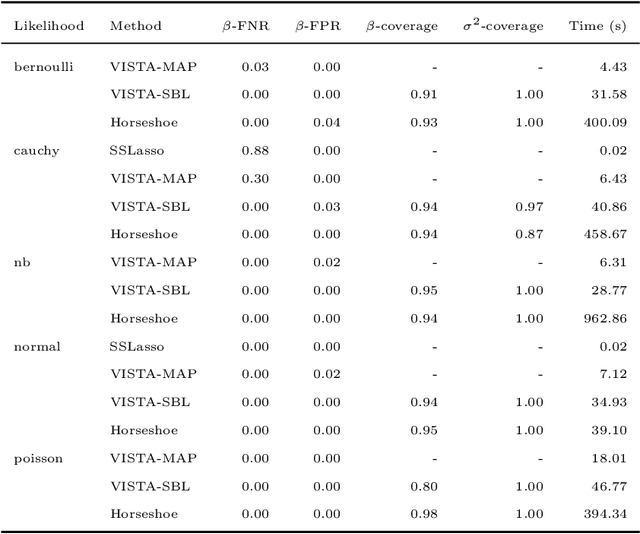
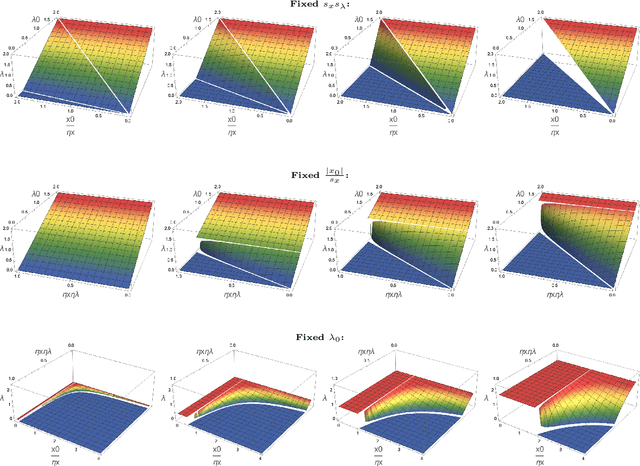
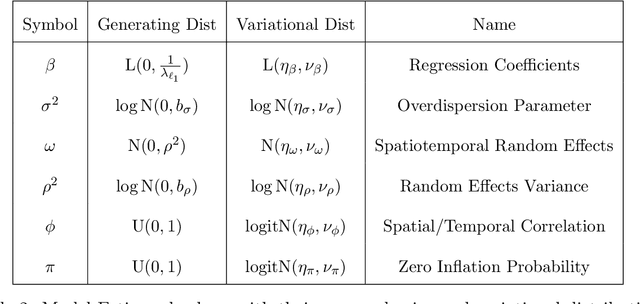
Modern statistical learning algorithms are capable of amazing flexibility, but struggle with interpretability. One possible solution is sparsity: making inference such that many of the parameters are estimated as being identically 0, which may be imposed through the use of nonsmooth penalties such as the $\ell_1$ penalty. However, the $\ell_1$ penalty introduces significant bias when high sparsity is desired. In this article, we retain the $\ell_1$ penalty, but define learnable penalty weights $\lambda_p$ endowed with hyperpriors. We start the article by investigating the optimization problem this poses, developing a proximal operator associated with the $\ell_1$ norm. We then study the theoretical properties of this variable-coefficient $\ell_1$ penalty in the context of penalized likelihood. Next, we investigate application of this penalty to Variational Bayes, developing a model we call the Sparse Bayesian Lasso which allows for behavior qualitatively like Lasso regression to be applied to arbitrary variational models. In simulation studies, this gives us the Uncertainty Quantification and low bias properties of simulation-based approaches with an order of magnitude less computation. Finally, we apply our methodology to a Bayesian lagged spatiotemporal regression model of internal displacement that occurred during the Iraqi Civil War of 2013-2017.

Subgroup Discovery in Unstructured Data

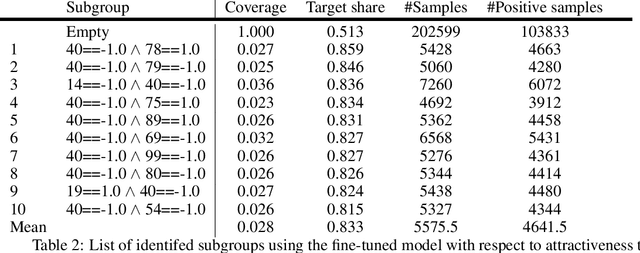
Subgroup discovery is a descriptive and exploratory data mining technique to identify subgroups in a population that exhibit interesting behavior with respect to a variable of interest. Subgroup discovery has numerous applications in knowledge discovery and hypothesis generation, yet it remains inapplicable for unstructured, high-dimensional data such as images. This is because subgroup discovery algorithms rely on defining descriptive rules based on (attribute, value) pairs, however, in unstructured data, an attribute is not well defined. Even in cases where the notion of attribute intuitively exists in the data, such as a pixel in an image, due to the high dimensionality of the data, these attributes are not informative enough to be used in a rule. In this paper, we introduce the subgroup-aware variational autoencoder, a novel variational autoencoder that learns a representation of unstructured data which leads to subgroups with higher quality. Our experimental results demonstrate the effectiveness of the method at learning subgroups with high quality while supporting the interpretability of the concepts.