Regression Trees Know Calculus
Paper and Code
May 22, 2024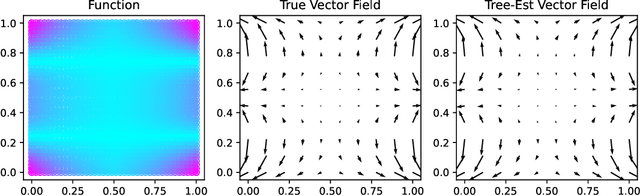
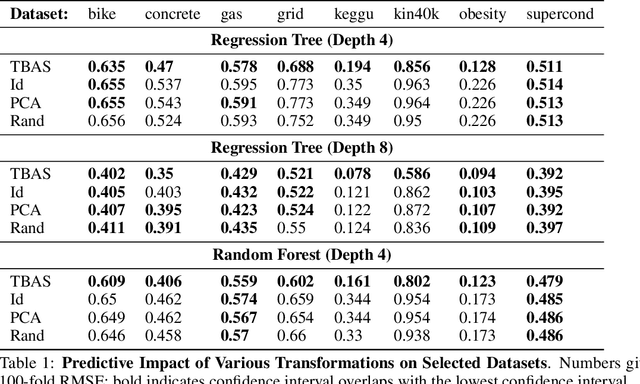
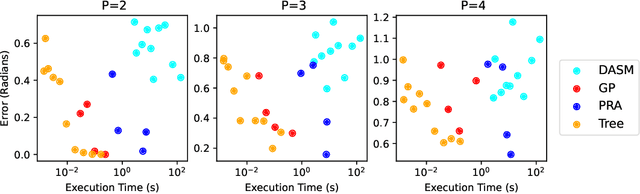

Regression trees have emerged as a preeminent tool for solving real-world regression problems due to their ability to deal with nonlinearities, interaction effects and sharp discontinuities. In this article, we rather study regression trees applied to well-behaved, differentiable functions, and determine the relationship between node parameters and the local gradient of the function being approximated. We find a simple estimate of the gradient which can be efficiently computed using quantities exposed by popular tree learning libraries. This allows the tools developed in the context of differentiable algorithms, like neural nets and Gaussian processes, to be deployed to tree-based models. To demonstrate this, we study measures of model sensitivity defined in terms of integrals of gradients and demonstrate how to compute them for regression trees using the proposed gradient estimates. Quantitative and qualitative numerical experiments reveal the capability of gradients estimated by regression trees to improve predictive analysis, solve tasks in uncertainty quantification, and provide interpretation of model behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge