Active Learning of Piecewise Gaussian Process Surrogates

Active learning of Gaussian process (GP) surrogates has been useful for optimizing experimental designs for physical/computer simulation experiments, and for steering data acquisition schemes in machine learning. In this paper, we develop a method for active learning of piecewise, Jump GP surrogates. Jump GPs are continuous within, but discontinuous across, regions of a design space, as required for applications spanning autonomous materials design, configuration of smart factory systems, and many others. Although our active learning heuristics are appropriated from strategies originally designed for ordinary GPs, we demonstrate that additionally accounting for model bias, as opposed to the usual model uncertainty, is essential in the Jump GP context. Toward that end, we develop an estimator for bias and variance of Jump GP models. Illustrations, and evidence of the advantage of our proposed methods, are provided on a suite of synthetic benchmarks, and real-simulation experiments of varying complexity.

Gaussian Process Model for Estimating Piecewise Continuous Regression Functions

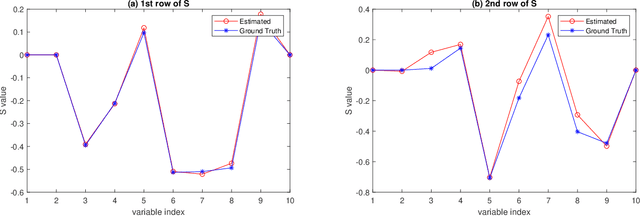
This paper presents a Gaussian process (GP) model for estimating piecewise continuous regression functions. In scientific and engineering applications of regression analysis, the underlying regression functions are piecewise continuous in that data follow different continuous regression models for different regions of the data with possible discontinuities between the regions. However, many conventional GP regression approaches are not designed for piecewise regression analysis. We propose a new GP modeling approach for estimating an unknown piecewise continuous regression function. The new GP model seeks for a local GP estimate of an unknown regression function at each test location, using local data neighboring to the test location. To accommodate the possibilities of the local data from different regions, the local data is partitioned into two sides by a local linear boundary, and only the local data belonging to the same side as the test location is used for the regression estimate. This local split works very well when the input regions are bounded by smooth boundaries, so the local linear approximation of the smooth boundaries works well. We estimate the local linear boundary jointly with the other hyperparameters of the GP model, using the maximum likelihood approach. Its computation time is as low as the local GP's time. The superior numerical performance of the proposed approach over the conventional GP modeling approaches is shown using various simulated piecewise regression functions.

Data Science for Motion and Time Analysis with Modern Motion Sensor Data

The motion-and-time analysis has been a popular research topic in operations research, especially for analyzing work performances in manufacturing and service operations. It is regaining attention as continuous improvement tools for lean manufacturing and smart factory. This paper develops a framework for data-driven analysis of work motions and studies their correlations to work speeds or execution rates, using data collected from modern motion sensors. The past analyses largely relied on manual steps involving time-consuming stop-watching and video-taping, followed by manual data analysis. While modern sensing devices have automated the collection of motion data, the motion analytics that transform the new data into knowledge are largely underdeveloped. Unsolved technical questions include: How the motion and time information can be extracted from the motion sensor data, how work motions and execution rates are statistically modeled and compared, and what are the statistical correlations of motions to the rates? In this paper, we develop a novel mathematical framework for motion and time analysis with motion sensor data, by defining new mathematical representation spaces of human motions and execution rates and by developing statistical tools on these new spaces. This methodological research is demonstrated using five use cases applied to manufacturing motion data.

Variable selection for Gaussian process regression through a sparse projection

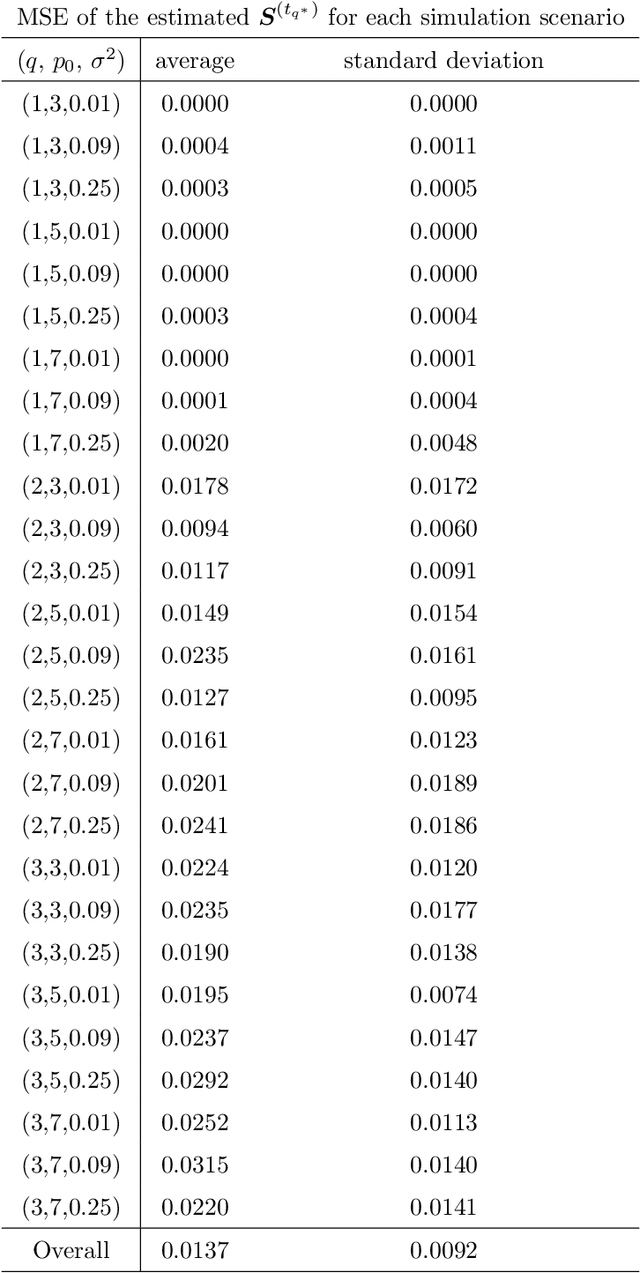
This paper presents a new variable selection approach integrated with Gaussian process (GP) regression. We consider a sparse projection of input variables and a general stationary covariance model that depends on the Euclidean distance between the projected features. The sparse projection matrix is considered as an unknown parameter. We propose a forward stagewise approach with embedded gradient descent steps to co-optimize the parameter with other covariance parameters based on the maximization of a non-convex marginal likelihood function with a concave sparsity penalty, and some convergence properties of the algorithm are provided. The proposed model covers a broader class of stationary covariance functions than the existing automatic relevance determination approaches, and the solution approach is more computationally feasible than the existing MCMC sampling procedures for the automatic relevance parameter estimation with a sparsity prior. The approach is evaluated for a large number of simulated scenarios. The choice of tuning parameters and the accuracy of the parameter estimation are evaluated with the simulation study. In the comparison to some chosen benchmark approaches, the proposed approach has provided a better accuracy in the variable selection. It is applied to an important problem of identifying environmental factors that affect an atmospheric corrosion of metal alloys.

Robust Gaussian Process Regression with a Bias Model

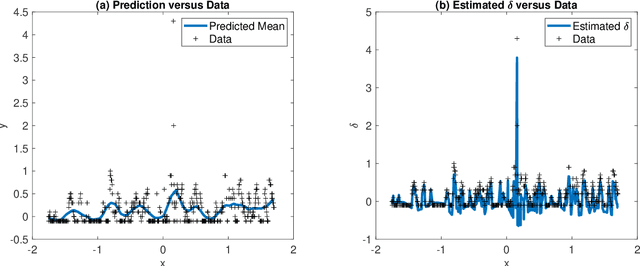
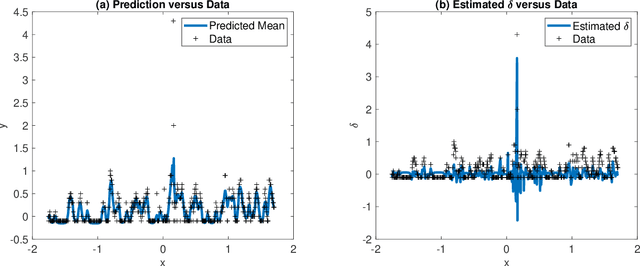
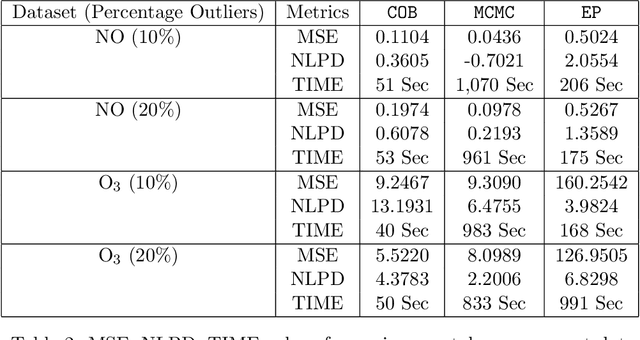
This paper presents a new approach to a robust Gaussian process (GP) regression. Most existing approaches replace an outlier-prone Gaussian likelihood with a non-Gaussian likelihood induced from a heavy tail distribution, such as the Laplace distribution and Student-t distribution. However, the use of a non-Gaussian likelihood would incur the need for a computationally expensive Bayesian approximate computation in the posterior inferences. The proposed approach models an outlier as a noisy and biased observation of an unknown regression function, and accordingly, the likelihood contains bias terms to explain the degree of deviations from the regression function. We entail how the biases can be estimated accurately with other hyperparameters by a regularized maximum likelihood estimation. Conditioned on the bias estimates, the robust GP regression can be reduced to a standard GP regression problem with analytical forms of the predictive mean and variance estimates. Therefore, the proposed approach is simple and very computationally attractive. It also gives a very robust and accurate GP estimate for many tested scenarios. For the numerical evaluation, we perform a comprehensive simulation study to evaluate the proposed approach with the comparison to the existing robust GP approaches under various simulated scenarios of different outlier proportions and different noise levels. The approach is applied to data from two measurement systems, where the predictors are based on robust environmental parameter measurements and the response variables utilize more complex chemical sensing methods that contain a certain percentage of outliers. The utility of the measurement systems and value of the environmental data are improved through the computationally efficient GP regression and bias model.

Sequential Adaptive Design for Jump Regression Estimation

Selecting input data or design points for statistical models has been of great interest in sequential design and active learning. In this paper, we present a new strategy of selecting the design points for a regression model when the underlying regression function is discontinuous. Two main motivating examples are (1) compressed material imaging with the purpose of accelerating the imaging speed and (2) design for regression analysis over a phase diagram in chemistry. In both examples, the underlying regression functions have discontinuities, so many of the existing design optimization approaches cannot be applied for the two examples because they mostly assume a continuous regression function. There are some studies for estimating a discontinuous regression function from its noisy observations, but all noisy observations are typically provided in advance in these studies. In this paper, we develop a design strategy of selecting the design points for regression analysis with discontinuities. We first review the existing approaches relevant to design optimization and active learning for regression analysis and discuss their limitations in handling a discontinuous regression function. We then present our novel design strategy for a regression analysis with discontinuities: some statistical properties with a fixed design will be presented first, and then these properties will be used to propose a new criterion of selecting the design points for the regression analysis. Sequential design of experiments with the new criterion will be presented with numerical examples.

Sparse Filtered SIRT for Electron Tomography

Electron tomographic reconstruction is a method for obtaining a three-dimensional image of a specimen with a series of two dimensional microscope images taken from different viewing angles. Filtered backprojection, one of the most popular tomographic reconstruction methods, does not work well under the existence of image noises and missing wedges. This paper presents a new approach to largely mitigate the effect of noises and missing wedges. We propose a novel filtered backprojection that optimizes the filter of the backprojection operator in terms of a reconstruction error. This data-dependent filter adaptively chooses the spectral domains of signals and noises, suppressing the noise frequency bands, so it is very effective in denoising. We also propose the new filtered backprojection embedded within the simultaneous iterative reconstruction iteration for mitigating the effect of missing wedges. Our numerical study is presented to show the performance gain of the proposed approach over the state-of-the-art.

Patchwork Kriging for Large-scale Gaussian Process Regression

This paper presents a new approach for Gaussian process (GP) regression for large datasets. The approach involves partitioning the regression input domain into multiple local regions with a different local GP model fitted in each region. Unlike existing local partitioned GP approaches, we introduce a technique for patching together the local GP models nearly seamlessly to ensure that the local GP models for two neighboring regions produce nearly the same response prediction and prediction error variance on the boundary between the two regions. This largely mitigates the well-known discontinuity problem that degrades the boundary accuracy of existing local partitioned GP methods. Our main innovation is to represent the continuity conditions as additional pseudo-observations that the differences between neighboring GP responses are identically zero at an appropriately chosen set of boundary input locations. To predict the response at any input location, we simply augment the actual response observations with the pseudo-observations and apply standard GP prediction methods to the augmented data. In contrast to heuristic continuity adjustments, this has an advantage of working within a formal GP framework, so that the GP-based predictive uncertainty quantification remains valid. Our approach also inherits a sparse block-like structure for the sample covariance matrix, which results in computationally efficient closed-form expressions for the predictive mean and variance. In addition, we provide a new spatial partitioning scheme based on a recursive space partitioning along local principal component directions, which makes the proposed approach applicable for regression domains having more than two dimensions. Using three spatial datasets and three higher dimensional datasets, we investigate the numerical performance of the approach and compare it to several state-of-the-art approaches.

Two-Level Structural Sparsity Regularization for Identifying Lattices and Defects in Noisy Images

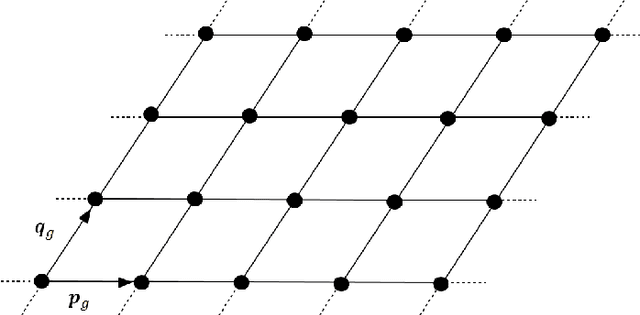
This paper presents a regularized regression model with a two-level structural sparsity penalty applied to locate individual atoms in a noisy scanning transmission electron microscopy image (STEM). In crystals, the locations of atoms is symmetric, condensed into a few lattice groups. Therefore, by identifying the underlying lattice in a given image, individual atoms can be accurately located. We propose to formulate the identification of the lattice groups as a sparse group selection problem. Furthermore, real atomic scale images contain defects and vacancies, so atomic identification based solely on a lattice group may result in false positives and false negatives. To minimize error, model includes an individual sparsity regularization in addition to the group sparsity for a within-group selection, which results in a regression model with a two-level sparsity regularization. We propose a modification of the group orthogonal matching pursuit (gOMP) algorithm with a thresholding step to solve the atom finding problem. The convergence and statistical analyses of the proposed algorithm are presented. The proposed algorithm is also evaluated through numerical experiments with simulated images. The applicability of the algorithm on determination of atom structures and identification of imaging distortions and atomic defects was demonstrated using three real STEM images. We believe this is an important step toward automatic phase identification and assignment with the advent of genomic databases for materials.

Robust Regression For Image Binarization Under Heavy Noises and Nonuniform Background

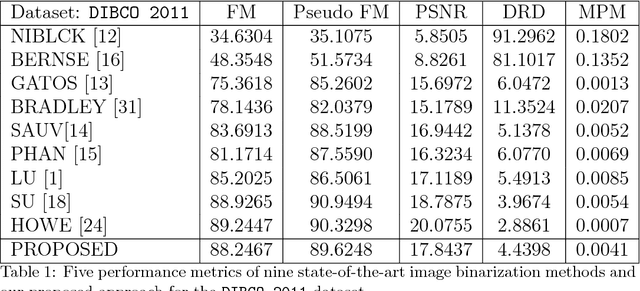
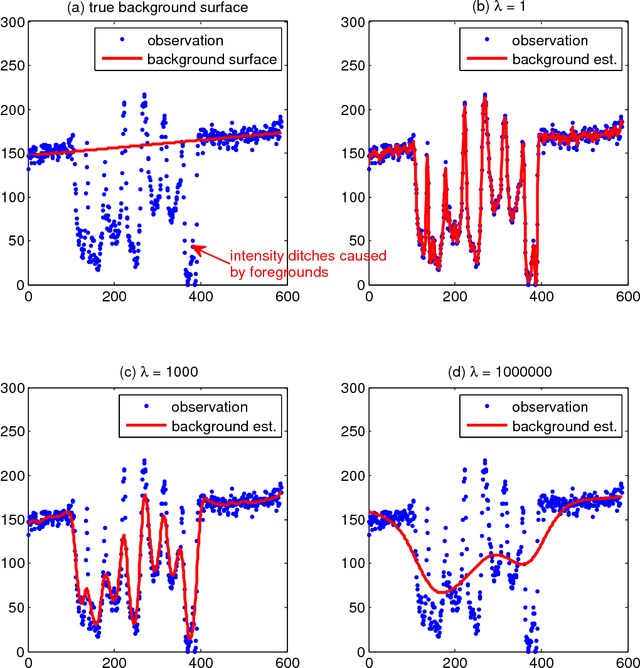
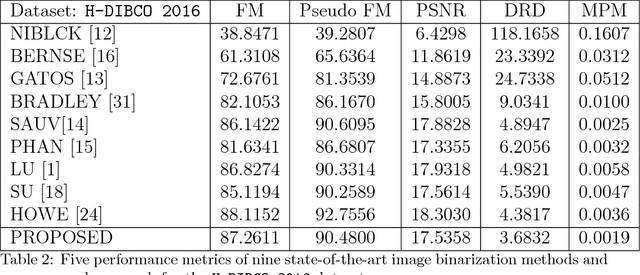
This paper presents a robust regression approach for image binarization under significant background variations and observation noises. The work is motivated by the need of identifying foreground regions in noisy microscopic image or degraded document images, where significant background variation and severe noise make an image binarization challenging. The proposed method first estimates the background of an input image, subtracts the estimated background from the input image, and apply a global thresholding to the subtracted outcome for achieving a binary image of foregrounds. A robust regression approach was proposed to estimate the background intensity surface with minimal effects of foreground intensities and noises, and a global threshold selector was proposed on the basis of a model selection criterion in a sparse regression. The proposed approach was validated using 26 test images and the corresponding ground truths, and the outcomes of the proposed work were compared with those from nine existing image binarization methods. The approach was also combined with three state-of-the-art morphological segmentation methods to show how the proposed approach can improve their image segmentation outcomes.