Robust Regression For Image Binarization Under Heavy Noises and Nonuniform Background

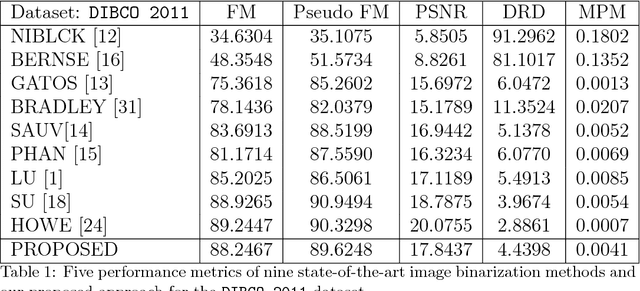
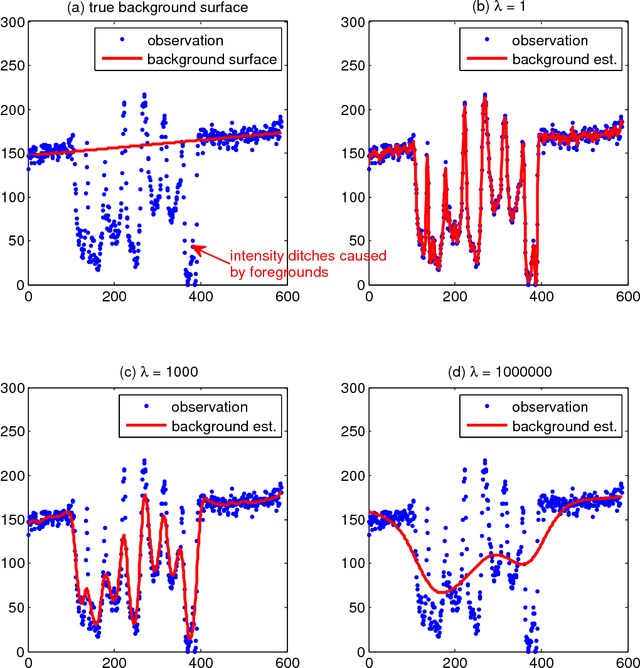
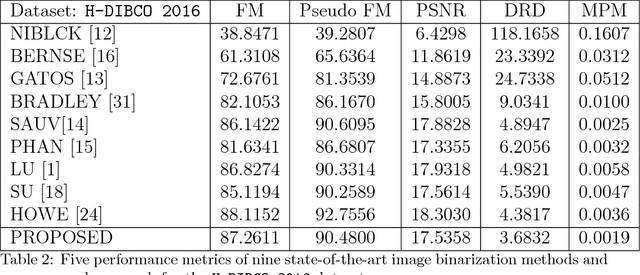
This paper presents a robust regression approach for image binarization under significant background variations and observation noises. The work is motivated by the need of identifying foreground regions in noisy microscopic image or degraded document images, where significant background variation and severe noise make an image binarization challenging. The proposed method first estimates the background of an input image, subtracts the estimated background from the input image, and apply a global thresholding to the subtracted outcome for achieving a binary image of foregrounds. A robust regression approach was proposed to estimate the background intensity surface with minimal effects of foreground intensities and noises, and a global threshold selector was proposed on the basis of a model selection criterion in a sparse regression. The proposed approach was validated using 26 test images and the corresponding ground truths, and the outcomes of the proposed work were compared with those from nine existing image binarization methods. The approach was also combined with three state-of-the-art morphological segmentation methods to show how the proposed approach can improve their image segmentation outcomes.

Sparse additive Gaussian process with soft interactions

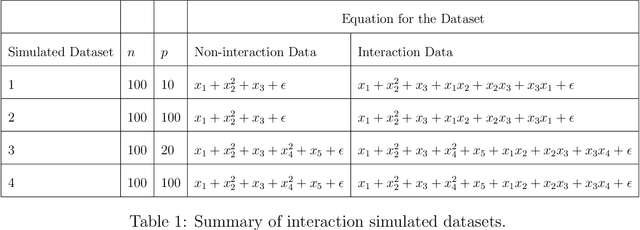
Additive nonparametric regression models provide an attractive tool for variable selection in high dimensions when the relationship between the response and predictors is complex. They offer greater flexibility compared to parametric non-linear regression models and better interpretability and scalability than the non-parametric regression models. However, achieving sparsity simultaneously in the number of nonparametric components as well as in the variables within each nonparametric component poses a stiff computational challenge. In this article, we develop a novel Bayesian additive regression model using a combination of hard and soft shrinkages to separately control the number of additive components and the variables within each component. An efficient algorithm is developed to select the importance variables and estimate the interaction network. Excellent performance is obtained in simulated and real data examples.