Sparse additive Gaussian process with soft interactions
Paper and Code
Jul 09, 2016


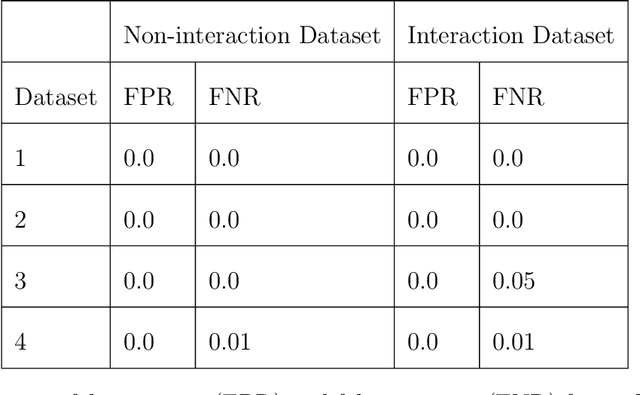
Additive nonparametric regression models provide an attractive tool for variable selection in high dimensions when the relationship between the response and predictors is complex. They offer greater flexibility compared to parametric non-linear regression models and better interpretability and scalability than the non-parametric regression models. However, achieving sparsity simultaneously in the number of nonparametric components as well as in the variables within each nonparametric component poses a stiff computational challenge. In this article, we develop a novel Bayesian additive regression model using a combination of hard and soft shrinkages to separately control the number of additive components and the variables within each component. An efficient algorithm is developed to select the importance variables and estimate the interaction network. Excellent performance is obtained in simulated and real data examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge