Variable selection for Gaussian process regression through a sparse projection
Paper and Code
Aug 25, 2020

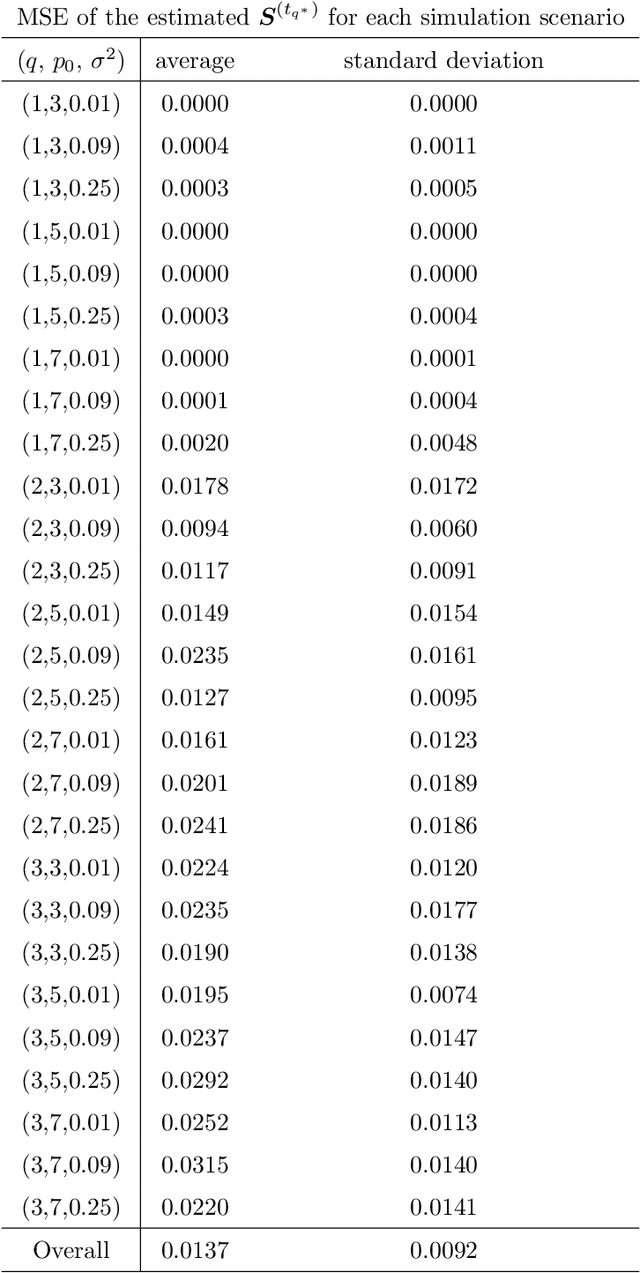
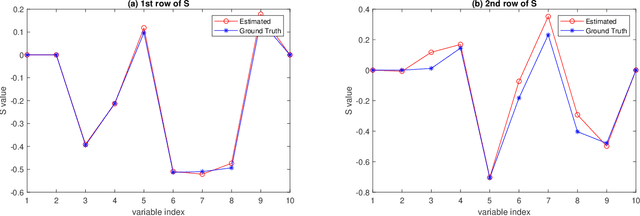
This paper presents a new variable selection approach integrated with Gaussian process (GP) regression. We consider a sparse projection of input variables and a general stationary covariance model that depends on the Euclidean distance between the projected features. The sparse projection matrix is considered as an unknown parameter. We propose a forward stagewise approach with embedded gradient descent steps to co-optimize the parameter with other covariance parameters based on the maximization of a non-convex marginal likelihood function with a concave sparsity penalty, and some convergence properties of the algorithm are provided. The proposed model covers a broader class of stationary covariance functions than the existing automatic relevance determination approaches, and the solution approach is more computationally feasible than the existing MCMC sampling procedures for the automatic relevance parameter estimation with a sparsity prior. The approach is evaluated for a large number of simulated scenarios. The choice of tuning parameters and the accuracy of the parameter estimation are evaluated with the simulation study. In the comparison to some chosen benchmark approaches, the proposed approach has provided a better accuracy in the variable selection. It is applied to an important problem of identifying environmental factors that affect an atmospheric corrosion of metal alloys.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge