Chad N. Hunter
Variable selection for Gaussian process regression through a sparse projection
Aug 25, 2020

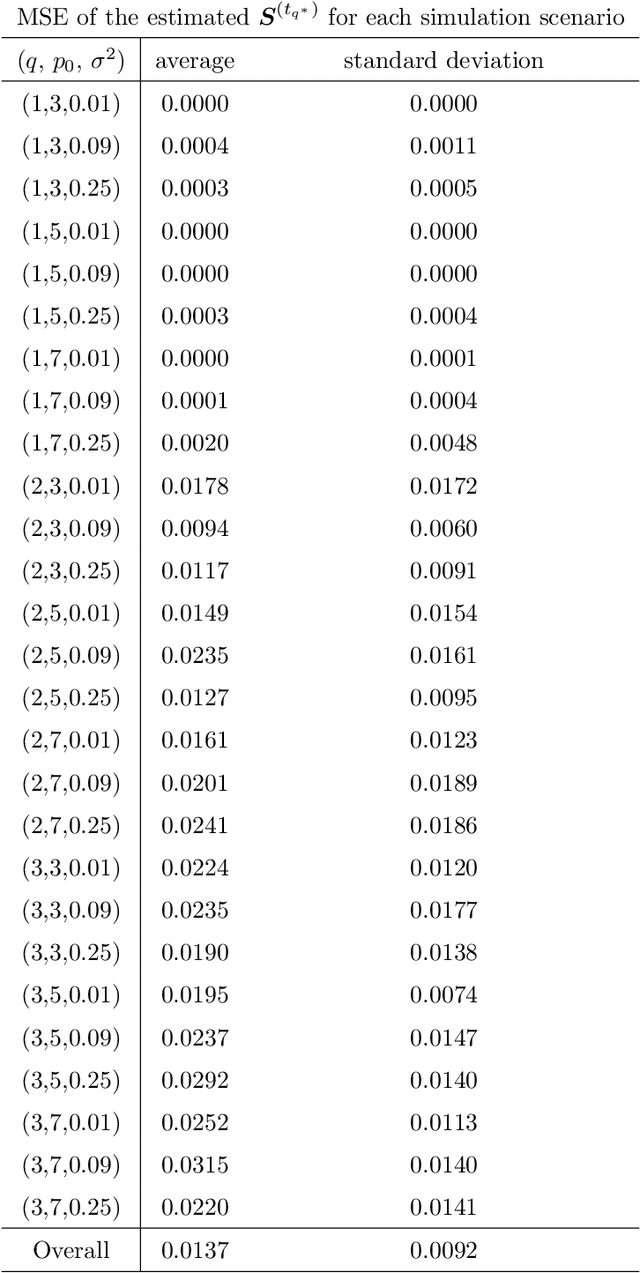
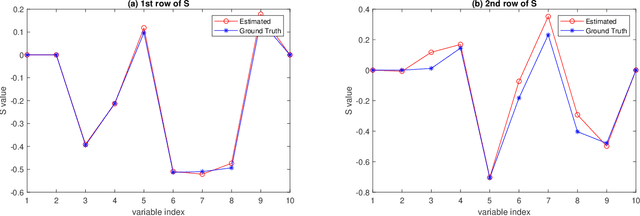
Abstract:This paper presents a new variable selection approach integrated with Gaussian process (GP) regression. We consider a sparse projection of input variables and a general stationary covariance model that depends on the Euclidean distance between the projected features. The sparse projection matrix is considered as an unknown parameter. We propose a forward stagewise approach with embedded gradient descent steps to co-optimize the parameter with other covariance parameters based on the maximization of a non-convex marginal likelihood function with a concave sparsity penalty, and some convergence properties of the algorithm are provided. The proposed model covers a broader class of stationary covariance functions than the existing automatic relevance determination approaches, and the solution approach is more computationally feasible than the existing MCMC sampling procedures for the automatic relevance parameter estimation with a sparsity prior. The approach is evaluated for a large number of simulated scenarios. The choice of tuning parameters and the accuracy of the parameter estimation are evaluated with the simulation study. In the comparison to some chosen benchmark approaches, the proposed approach has provided a better accuracy in the variable selection. It is applied to an important problem of identifying environmental factors that affect an atmospheric corrosion of metal alloys.
Robust Gaussian Process Regression with a Bias Model
Jan 14, 2020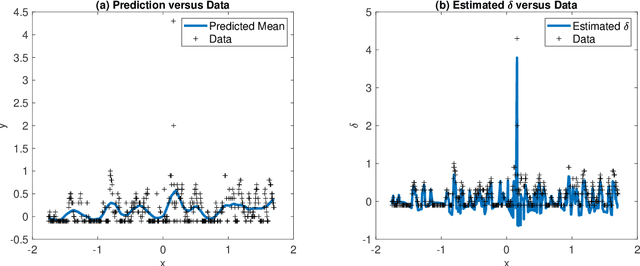

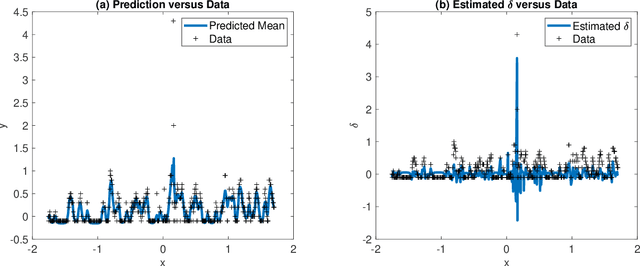
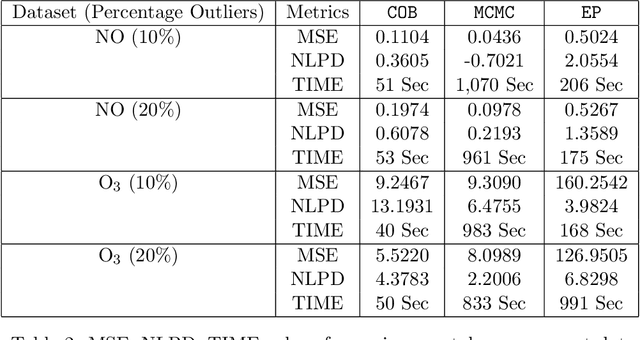
Abstract:This paper presents a new approach to a robust Gaussian process (GP) regression. Most existing approaches replace an outlier-prone Gaussian likelihood with a non-Gaussian likelihood induced from a heavy tail distribution, such as the Laplace distribution and Student-t distribution. However, the use of a non-Gaussian likelihood would incur the need for a computationally expensive Bayesian approximate computation in the posterior inferences. The proposed approach models an outlier as a noisy and biased observation of an unknown regression function, and accordingly, the likelihood contains bias terms to explain the degree of deviations from the regression function. We entail how the biases can be estimated accurately with other hyperparameters by a regularized maximum likelihood estimation. Conditioned on the bias estimates, the robust GP regression can be reduced to a standard GP regression problem with analytical forms of the predictive mean and variance estimates. Therefore, the proposed approach is simple and very computationally attractive. It also gives a very robust and accurate GP estimate for many tested scenarios. For the numerical evaluation, we perform a comprehensive simulation study to evaluate the proposed approach with the comparison to the existing robust GP approaches under various simulated scenarios of different outlier proportions and different noise levels. The approach is applied to data from two measurement systems, where the predictors are based on robust environmental parameter measurements and the response variables utilize more complex chemical sensing methods that contain a certain percentage of outliers. The utility of the measurement systems and value of the environmental data are improved through the computationally efficient GP regression and bias model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge