Scalable Gaussian Processes for Data-Driven Design using Big Data with Categorical Factors

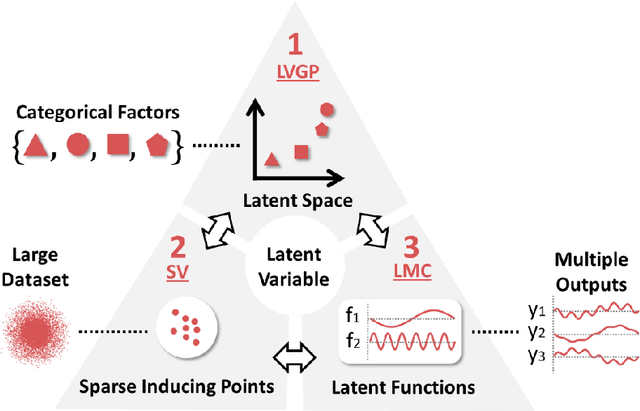
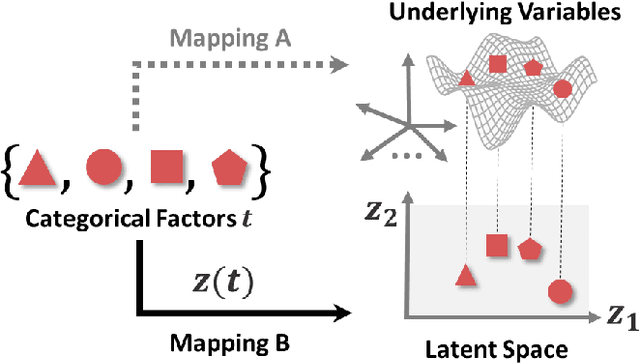
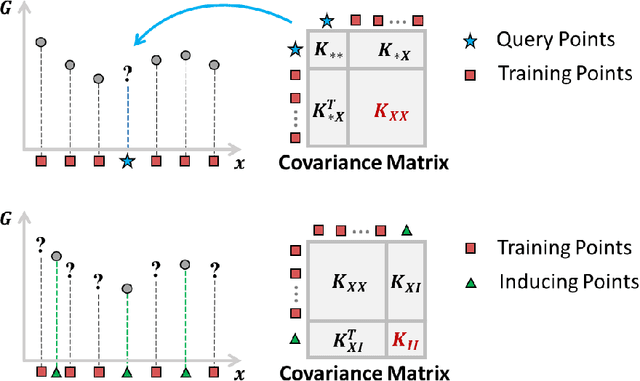
Scientific and engineering problems often require the use of artificial intelligence to aid understanding and the search for promising designs. While Gaussian processes (GP) stand out as easy-to-use and interpretable learners, they have difficulties in accommodating big datasets, categorical inputs, and multiple responses, which has become a common challenge for a growing number of data-driven design applications. In this paper, we propose a GP model that utilizes latent variables and functions obtained through variational inference to address the aforementioned challenges simultaneously. The method is built upon the latent variable Gaussian process (LVGP) model where categorical factors are mapped into a continuous latent space to enable GP modeling of mixed-variable datasets. By extending variational inference to LVGP models, the large training dataset is replaced by a small set of inducing points to address the scalability issue. Output response vectors are represented by a linear combination of independent latent functions, forming a flexible kernel structure to handle multiple responses that might have distinct behaviors. Comparative studies demonstrate that the proposed method scales well for large datasets with over 10^4 data points, while outperforming state-of-the-art machine learning methods without requiring much hyperparameter tuning. In addition, an interpretable latent space is obtained to draw insights into the effect of categorical factors, such as those associated with building blocks of architectures and element choices in metamaterial and materials design. Our approach is demonstrated for machine learning of ternary oxide materials and topology optimization of a multiscale compliant mechanism with aperiodic microstructures and multiple materials.

Bayesian Optimization for Materials Design with Mixed Quantitative and Qualitative Variables

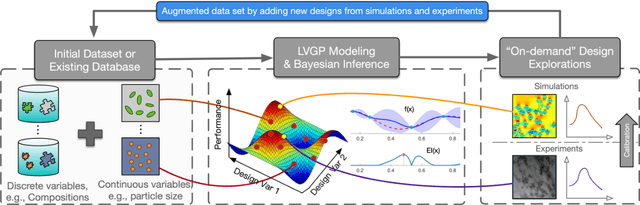
Although Bayesian Optimization (BO) has been employed for accelerating materials design in computational materials engineering, existing works are restricted to problems with quantitative variables. However, real designs of materials systems involve both qualitative and quantitative design variables representing material compositions, microstructure morphology, and processing conditions. For mixed-variable problems, existing Bayesian Optimization (BO) approaches represent qualitative factors by dummy variables first and then fit a standard Gaussian process (GP) model with numerical variables as the surrogate model. This approach is restrictive theoretically and fails to capture complex correlations between qualitative levels. We present in this paper the integration of a novel latent-variable (LV) approach for mixed-variable GP modeling with the BO framework for materials design. LVGP is a fundamentally different approach that maps qualitative design variables to underlying numerical LV in GP, which has strong physical justification. It provides flexible parameterization and representation of qualitative factors and shows superior modeling accuracy compared to the existing methods. We demonstrate our approach through testing with numerical examples and materials design examples. It is found that in all test examples the mapped LVs provide intuitive visualization and substantial insight into the nature and effects of the qualitative factors. Though materials designs are used as examples, the method presented is generic and can be utilized for other mixed variable design optimization problems that involve expensive physics-based simulations.

Patchwork Kriging for Large-scale Gaussian Process Regression

This paper presents a new approach for Gaussian process (GP) regression for large datasets. The approach involves partitioning the regression input domain into multiple local regions with a different local GP model fitted in each region. Unlike existing local partitioned GP approaches, we introduce a technique for patching together the local GP models nearly seamlessly to ensure that the local GP models for two neighboring regions produce nearly the same response prediction and prediction error variance on the boundary between the two regions. This largely mitigates the well-known discontinuity problem that degrades the boundary accuracy of existing local partitioned GP methods. Our main innovation is to represent the continuity conditions as additional pseudo-observations that the differences between neighboring GP responses are identically zero at an appropriately chosen set of boundary input locations. To predict the response at any input location, we simply augment the actual response observations with the pseudo-observations and apply standard GP prediction methods to the augmented data. In contrast to heuristic continuity adjustments, this has an advantage of working within a formal GP framework, so that the GP-based predictive uncertainty quantification remains valid. Our approach also inherits a sparse block-like structure for the sample covariance matrix, which results in computationally efficient closed-form expressions for the predictive mean and variance. In addition, we provide a new spatial partitioning scheme based on a recursive space partitioning along local principal component directions, which makes the proposed approach applicable for regression domains having more than two dimensions. Using three spatial datasets and three higher dimensional datasets, we investigate the numerical performance of the approach and compare it to several state-of-the-art approaches.