Emerging Microelectronic Materials by Design: Navigating Combinatorial Design Space with Scarce and Dispersed Data

The increasing demands of sustainable energy, electronics, and biomedical applications call for next-generation functional materials with unprecedented properties. Of particular interest are emerging materials that display exceptional physical properties, making them promising candidates in energy-efficient microelectronic devices. As the conventional Edisonian approach becomes significantly outpaced by growing societal needs, emerging computational modeling and machine learning (ML) methods are employed for the rational design of materials. However, the complex physical mechanisms, cost of first-principles calculations, and the dispersity and scarcity of data pose challenges to both physics-based and data-driven materials modeling. Moreover, the combinatorial composition-structure design space is high-dimensional and often disjoint, making design optimization nontrivial. In this Account, we review a team effort toward establishing a framework that integrates data-driven and physics-based methods to address these challenges and accelerate materials design. We begin by presenting our integrated materials design framework and its three components in a general context. We then provide an example of applying this materials design framework to metal-insulator transition (MIT) materials, a specific type of emerging materials with practical importance in next-generation memory technologies. We identify multiple new materials which may display this property and propose pathways for their synthesis. Finally, we identify some outstanding challenges in data-driven materials design, such as materials data quality issues and property-performance mismatch. We seek to raise awareness of these overlooked issues hindering materials design, thus stimulating efforts toward developing methods to mitigate the gaps.

Fully Bayesian inference for latent variable Gaussian process models

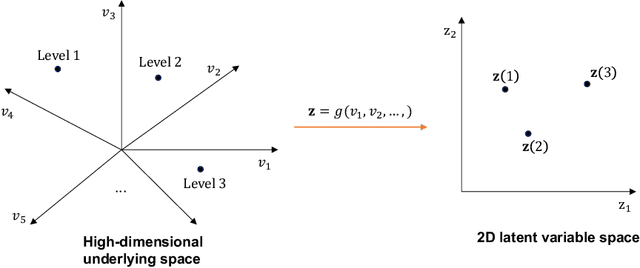
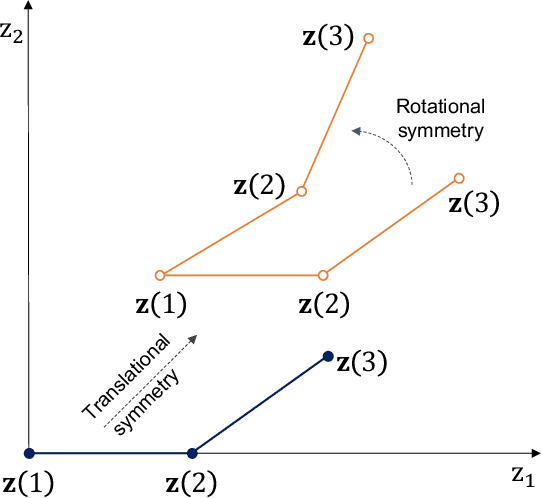
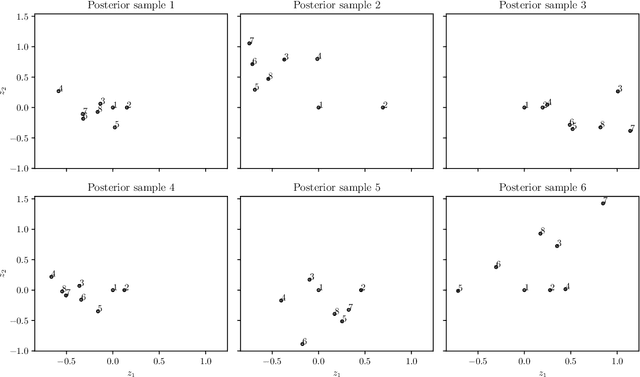
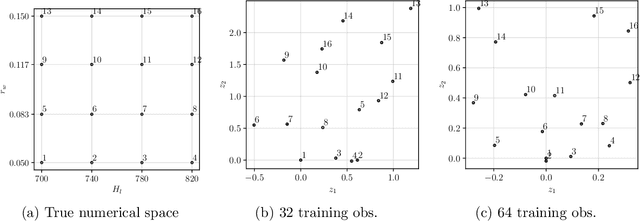
Real engineering and scientific applications often involve one or more qualitative inputs. Standard Gaussian processes (GPs), however, cannot directly accommodate qualitative inputs. The recently introduced latent variable Gaussian process (LVGP) overcomes this issue by first mapping each qualitative factor to underlying latent variables (LVs), and then uses any standard GP covariance function over these LVs. The LVs are estimated similarly to the other GP hyperparameters through maximum likelihood estimation, and then plugged into the prediction expressions. However, this plug-in approach will not account for uncertainty in estimation of the LVs, which can be significant especially with limited training data. In this work, we develop a fully Bayesian approach for the LVGP model and for visualizing the effects of the qualitative inputs via their LVs. We also develop approximations for scaling up LVGPs and fully Bayesian inference for the LVGP hyperparameters. We conduct numerical studies comparing plug-in inference against fully Bayesian inference over a few engineering models and material design applications. In contrast to previous studies on standard GP modeling that have largely concluded that a fully Bayesian treatment offers limited improvements, our results show that for LVGP modeling it offers significant improvements in prediction accuracy and uncertainty quantification over the plug-in approach.

Scalable Gaussian Processes for Data-Driven Design using Big Data with Categorical Factors

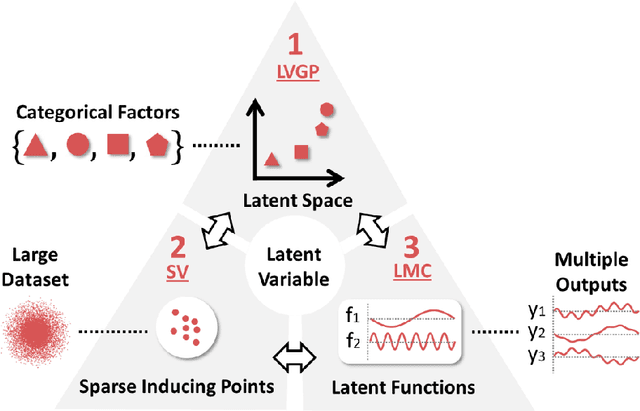
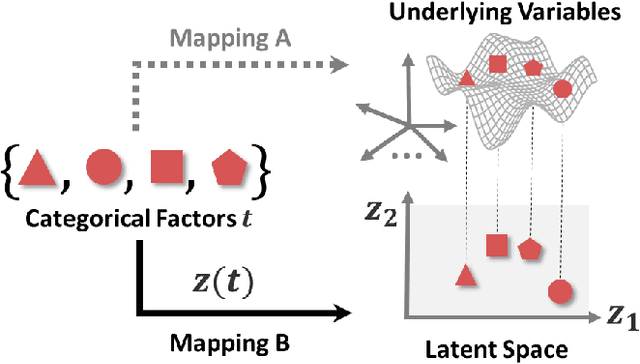
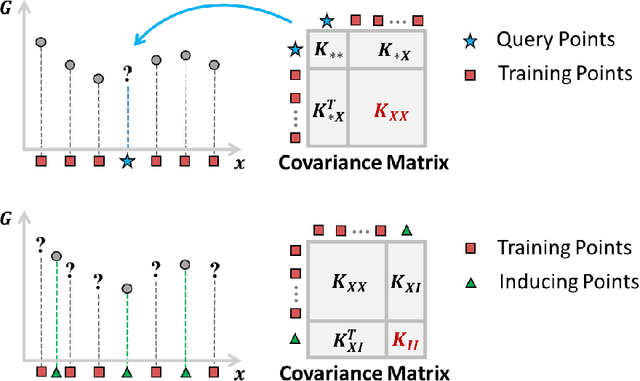
Scientific and engineering problems often require the use of artificial intelligence to aid understanding and the search for promising designs. While Gaussian processes (GP) stand out as easy-to-use and interpretable learners, they have difficulties in accommodating big datasets, categorical inputs, and multiple responses, which has become a common challenge for a growing number of data-driven design applications. In this paper, we propose a GP model that utilizes latent variables and functions obtained through variational inference to address the aforementioned challenges simultaneously. The method is built upon the latent variable Gaussian process (LVGP) model where categorical factors are mapped into a continuous latent space to enable GP modeling of mixed-variable datasets. By extending variational inference to LVGP models, the large training dataset is replaced by a small set of inducing points to address the scalability issue. Output response vectors are represented by a linear combination of independent latent functions, forming a flexible kernel structure to handle multiple responses that might have distinct behaviors. Comparative studies demonstrate that the proposed method scales well for large datasets with over 10^4 data points, while outperforming state-of-the-art machine learning methods without requiring much hyperparameter tuning. In addition, an interpretable latent space is obtained to draw insights into the effect of categorical factors, such as those associated with building blocks of architectures and element choices in metamaterial and materials design. Our approach is demonstrated for machine learning of ternary oxide materials and topology optimization of a multiscale compliant mechanism with aperiodic microstructures and multiple materials.