An End-to-end Planning Framework with Agentic LLMs and PDDL

We present an end-to-end framework for planning supported by verifiers. An orchestrator receives a human specification written in natural language and converts it into a PDDL (Planning Domain Definition Language) model, where the domain and problem are iteratively refined by sub-modules (agents) to address common planning requirements, such as time constraints and optimality, as well as ambiguities and contradictions that may exist in the human specification. The validated domain and problem are then passed to an external planning engine to generate a plan. The orchestrator and agents are powered by Large Language Models (LLMs) and require no human intervention at any stage of the process. Finally, a module translates the final plan back into natural language to improve human readability while maintaining the correctness of each step. We demonstrate the flexibility and effectiveness of our framework across various domains and tasks, including the Google NaturalPlan benchmark and PlanBench, as well as planning problems like Blocksworld and the Tower of Hanoi (where LLMs are known to struggle even with small instances). Our framework can be integrated with any PDDL planning engine and validator (such as Fast Downward, LPG, POPF, VAL, and uVAL, which we have tested) and represents a significant step toward end-to-end planning aided by LLMs.

Serving Large Language Models on Huawei CloudMatrix384

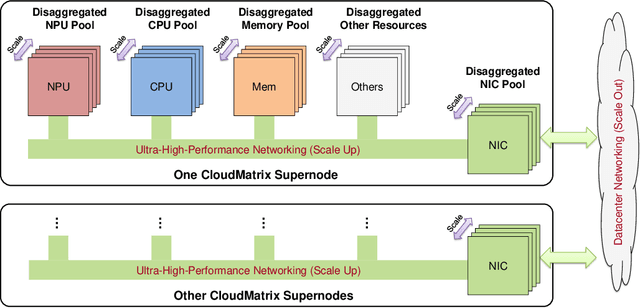
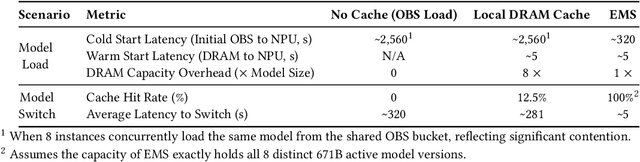
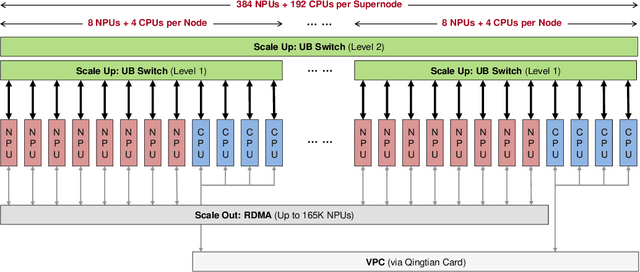
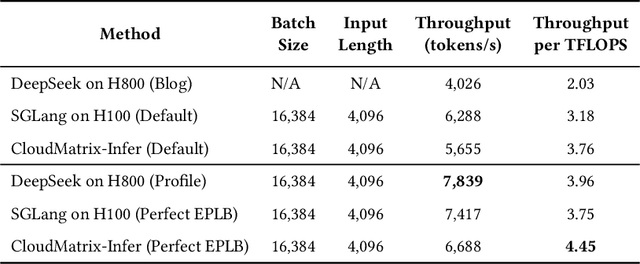
The rapid evolution of large language models (LLMs), driven by growing parameter scales, adoption of mixture-of-experts (MoE) architectures, and expanding context lengths, imposes unprecedented demands on AI infrastructure. Traditional AI clusters face limitations in compute intensity, memory bandwidth, inter-chip communication, and latency, compounded by variable workloads and strict service-level objectives. Addressing these issues requires fundamentally redesigned hardware-software integration. This paper introduces Huawei CloudMatrix, a next-generation AI datacenter architecture, realized in the production-grade CloudMatrix384 supernode. It integrates 384 Ascend 910C NPUs and 192 Kunpeng CPUs interconnected via an ultra-high-bandwidth Unified Bus (UB) network, enabling direct all-to-all communication and dynamic pooling of resources. These features optimize performance for communication-intensive operations, such as large-scale MoE expert parallelism and distributed key-value cache access. To fully leverage CloudMatrix384, we propose CloudMatrix-Infer, an advanced LLM serving solution incorporating three core innovations: a peer-to-peer serving architecture that independently scales prefill, decode, and caching; a large-scale expert parallelism strategy supporting EP320 via efficient UB-based token dispatch; and hardware-aware optimizations including specialized operators, microbatch-based pipelining, and INT8 quantization. Evaluation with the DeepSeek-R1 model shows CloudMatrix-Infer achieves state-of-the-art efficiency: prefill throughput of 6,688 tokens/s per NPU and decode throughput of 1,943 tokens/s per NPU (<50 ms TPOT). It effectively balances throughput and latency, sustaining 538 tokens/s even under stringent 15 ms latency constraints, while INT8 quantization maintains model accuracy across benchmarks.

Scalable Gaussian Processes for Data-Driven Design using Big Data with Categorical Factors

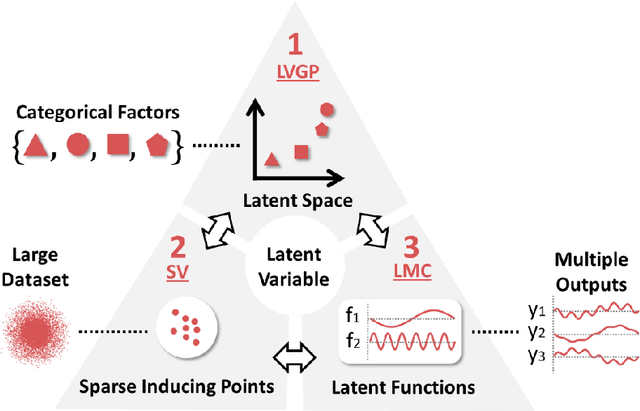
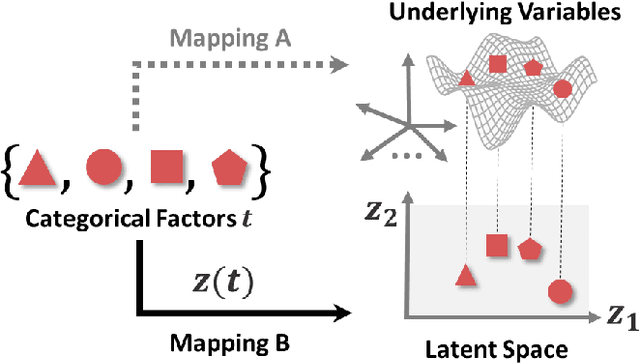
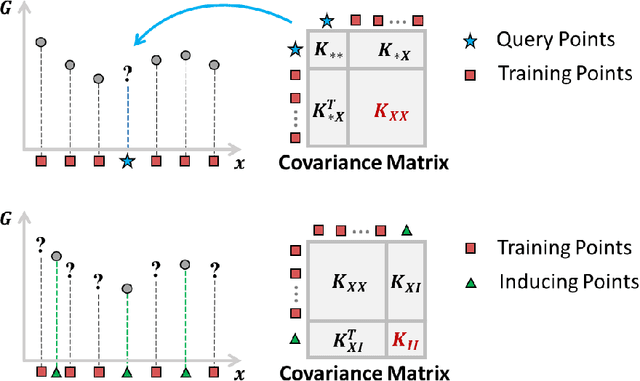
Scientific and engineering problems often require the use of artificial intelligence to aid understanding and the search for promising designs. While Gaussian processes (GP) stand out as easy-to-use and interpretable learners, they have difficulties in accommodating big datasets, categorical inputs, and multiple responses, which has become a common challenge for a growing number of data-driven design applications. In this paper, we propose a GP model that utilizes latent variables and functions obtained through variational inference to address the aforementioned challenges simultaneously. The method is built upon the latent variable Gaussian process (LVGP) model where categorical factors are mapped into a continuous latent space to enable GP modeling of mixed-variable datasets. By extending variational inference to LVGP models, the large training dataset is replaced by a small set of inducing points to address the scalability issue. Output response vectors are represented by a linear combination of independent latent functions, forming a flexible kernel structure to handle multiple responses that might have distinct behaviors. Comparative studies demonstrate that the proposed method scales well for large datasets with over 10^4 data points, while outperforming state-of-the-art machine learning methods without requiring much hyperparameter tuning. In addition, an interpretable latent space is obtained to draw insights into the effect of categorical factors, such as those associated with building blocks of architectures and element choices in metamaterial and materials design. Our approach is demonstrated for machine learning of ternary oxide materials and topology optimization of a multiscale compliant mechanism with aperiodic microstructures and multiple materials.

Data-Driven Multiscale Design of Cellular Composites with Multiclass Microstructures for Natural Frequency Maximization

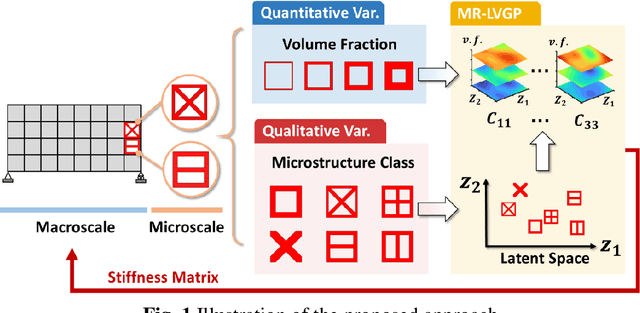
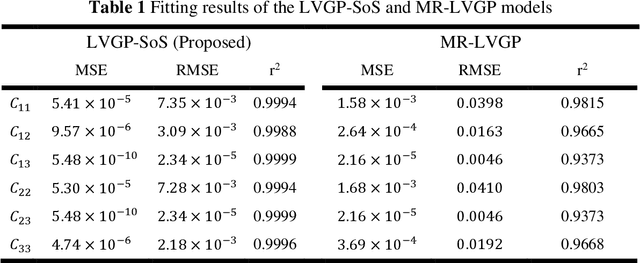
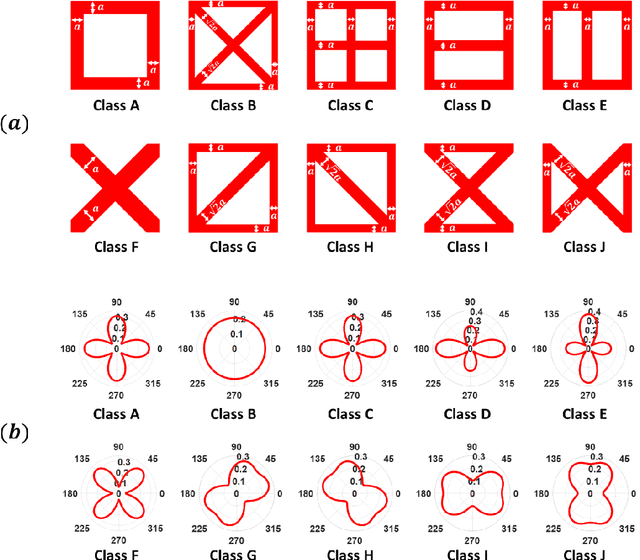
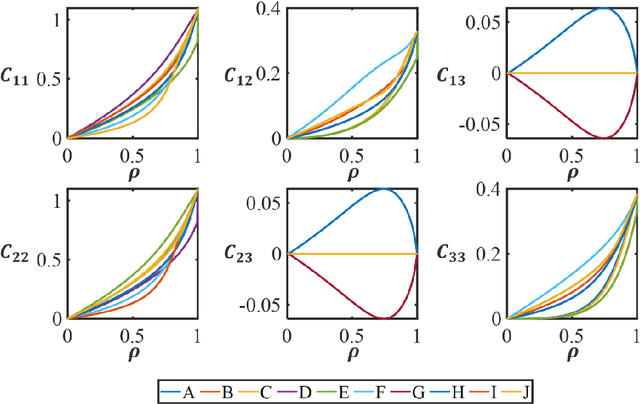
For natural frequency optimization of engineering structures, cellular composites have been shown to possess an edge over solid. However, existing multiscale design methods for cellular composites are either computationally exhaustive or confined to a single class of microstructures. In this paper, we propose a data-driven topology optimization (TO) approach to enable the multiscale design of cellular structures with various choices of microstructure classes. The key component is a newly proposed latent-variable Gaussian process (LVGP) model through which different classes of microstructures are mapped into a low-dimensional continuous latent space. It provides an interpretable distance metric between classes and captures their effects on the homogenized stiffness tensors. By introducing latent vectors as design variables, a differentiable transition of stiffness matrix between classes can be easily achieved with an analytical gradient. After integrating LVGP with the density-based TO, an efficient data-driven cellular composite optimization process is developed to enable concurrent exploration of microstructure concepts and the associated volume fractions for natural frequency optimization. Examples reveal that the proposed cellular designs with multiclass microstructures achieve higher natural frequencies than both single-scale and single-class designs. This framework can be easily extended to other multi-scale TO problems, such as thermal compliance and dynamic response optimization.

Deep Generative Modeling for Mechanistic-based Learning and Design of Metamaterial Systems

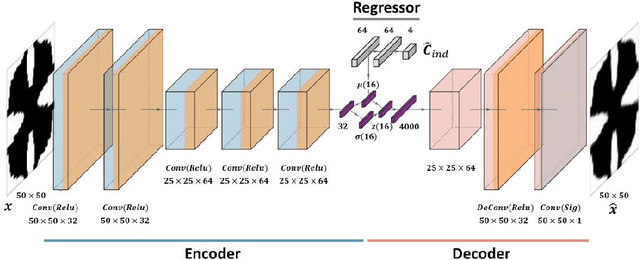
The inverse design of metamaterials is difficult due to a high-dimensional topological design space and presence of multiple local optima. Computational cost is even more demanding for design of multiscale metamaterial systems with aperiodic microstructures and spatially-varying or functionally gradient properties. Despite the growing interest in applying data-driven methods to address this hurdle, current methods either only focus on microstructure generation or adopt an unscalable framework for the multiscale design. In this study, we propose a novel data-driven metamaterial design framework based on deep generative modeling. A deep neural network model consisting of a variational autoencoder (VAE) and a regressor for property prediction is trained on a large metamaterial database to map complex microstructures into a low-dimensional, continuous and organized latent space. Our study shows several advantages of the VAE based generative model. First, the latent space of VAE provides a distance metric to measure shape similarity, enabling interpolation between microstructures and encoding meaningful patterns of variation in geometries and properties. For microstructure design, the tuning of mechanical properties and complex manipulations of microstructures are easily achieved by simple vector operations in the latent space. Second, the vector operation can be further extended to form metamaterial families with controlled gradation of mechanical properties. Third, for multiscale metamaterial systems design, a diverse set of microstructures can be rapidly generated based on target properties at different locations and then assembled by an efficient graph-based optimization method to ensure compatibility between adjacent microstructures. We demonstrate our framework by designing both functionally graded and heterogeneous metamaterial systems that achieve desired distortion behaviors.

Data-Driven Topology Optimization with Multiclass Microstructures using Latent Variable Gaussian Process

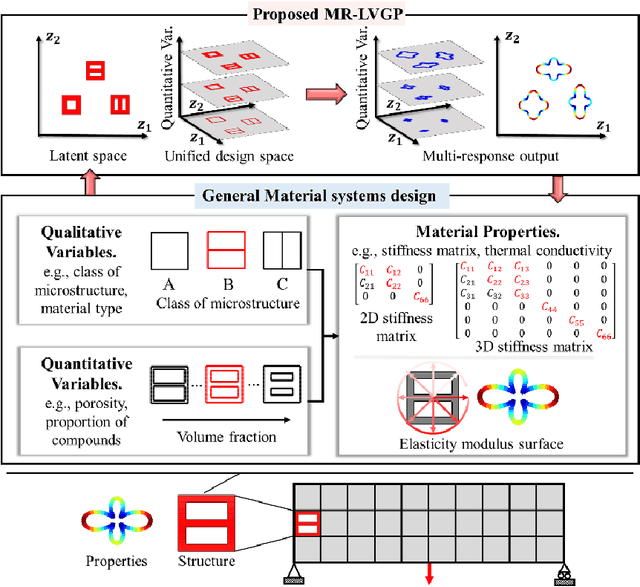
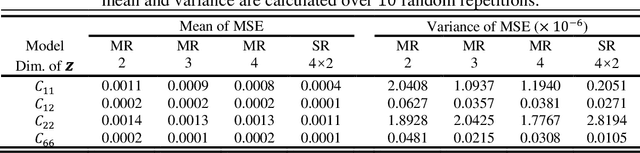
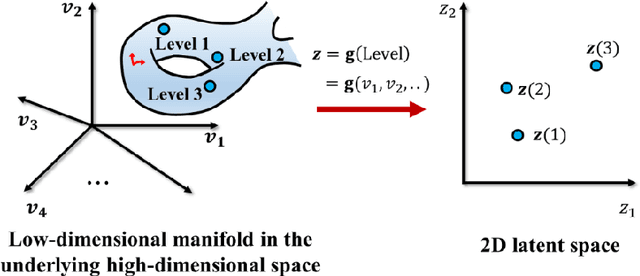
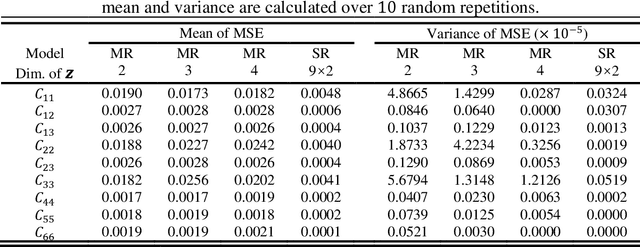
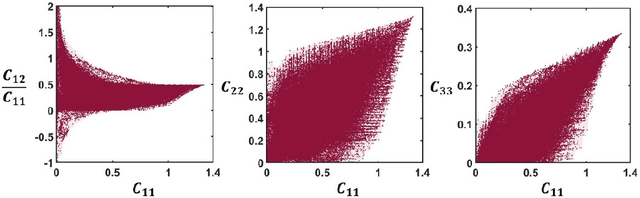
The data-driven approach is emerging as a promising method for the topological design of multiscale structures with greater efficiency. However, existing data-driven methods mostly focus on a single class of microstructures without considering multiple classes to accommodate spatially varying desired properties. The key challenge is the lack of an inherent ordering or distance measure between different classes of microstructures in meeting a range of properties. To overcome this hurdle, we extend the newly developed latent-variable Gaussian process (LVGP) models to create multi-response LVGP (MR-LVGP) models for the microstructure libraries of metamaterials, taking both qualitative microstructure concepts and quantitative microstructure design variables as mixed-variable inputs. The MR-LVGP model embeds the mixed variables into a continuous design space based on their collective effects on the responses, providing substantial insights into the interplay between different geometrical classes and material parameters of microstructures. With this model, we can easily obtain a continuous and differentiable transition between different microstructure concepts that can render gradient information for multiscale topology optimization. We demonstrate its benefits through multiscale topology optimization with aperiodic microstructures. Design examples reveal that considering multiclass microstructures can lead to improved performance due to the consistent load-transfer paths for micro- and macro-structures.

Operations on soft sets revisited

Soft sets, as a mathematical tool for dealing with uncertainty, have recently gained considerable attention, including some successful applications in information processing, decision, demand analysis, and forecasting. To construct new soft sets from given soft sets, some operations on soft sets have been proposed. Unfortunately, such operations cannot keep all classical set-theoretic laws true for soft sets. In this paper, we redefine the intersection, complement, and difference of soft sets and investigate the algebraic properties of these operations along with a known union operation. We find that the new operation system on soft sets inherits all basic properties of operations on classical sets, which justifies our definitions.

Information-theoretic measures associated with rough set approximations

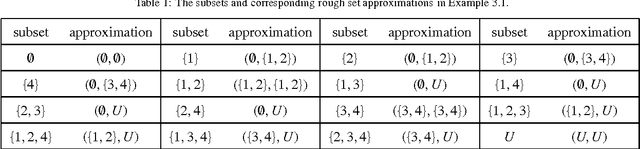
Although some information-theoretic measures of uncertainty or granularity have been proposed in rough set theory, these measures are only dependent on the underlying partition and the cardinality of the universe, independent of the lower and upper approximations. It seems somewhat unreasonable since the basic idea of rough set theory aims at describing vague concepts by the lower and upper approximations. In this paper, we thus define new information-theoretic entropy and co-entropy functions associated to the partition and the approximations to measure the uncertainty and granularity of an approximation space. After introducing the novel notions of entropy and co-entropy, we then examine their properties. In particular, we discuss the relationship of co-entropies between different universes. The theoretical development is accompanied by illustrative numerical examples.

Covering rough sets based on neighborhoods: An approach without using neighborhoods

Rough set theory, a mathematical tool to deal with inexact or uncertain knowledge in information systems, has originally described the indiscernibility of elements by equivalence relations. Covering rough sets are a natural extension of classical rough sets by relaxing the partitions arising from equivalence relations to coverings. Recently, some topological concepts such as neighborhood have been applied to covering rough sets. In this paper, we further investigate the covering rough sets based on neighborhoods by approximation operations. We show that the upper approximation based on neighborhoods can be defined equivalently without using neighborhoods. To analyze the coverings themselves, we introduce unary and composition operations on coverings. A notion of homomorphismis provided to relate two covering approximation spaces. We also examine the properties of approximations preserved by the operations and homomorphisms, respectively.

A note on communicating between information systems based on including degrees

In order to study the communication between information systems, Gong and Xiao [Z. Gong and Z. Xiao, Communicating between information systems based on including degrees, International Journal of General Systems 39 (2010) 189--206] proposed the concept of general relation mappings based on including degrees. Some properties and the extension for fuzzy information systems of the general relation mappings have been investigated there. In this paper, we point out by counterexamples that several assertions (Lemma 3.1, Lemma 3.2, Theorem 4.1, and Theorem 4.3) in the aforementioned work are not true in general.