Remixing Functionally Graded Structures: Data-Driven Topology Optimization with Multiclass Shape Blending

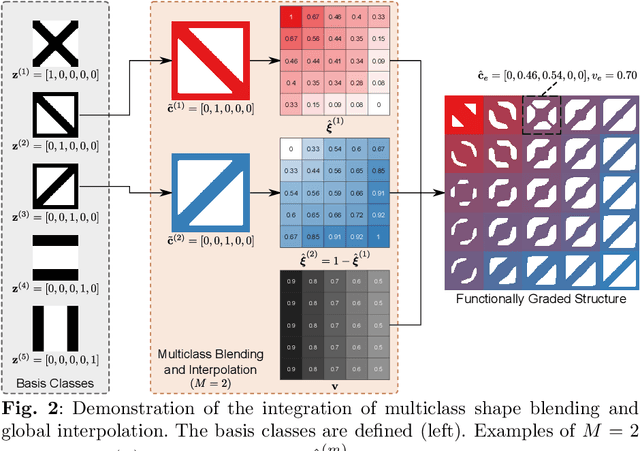
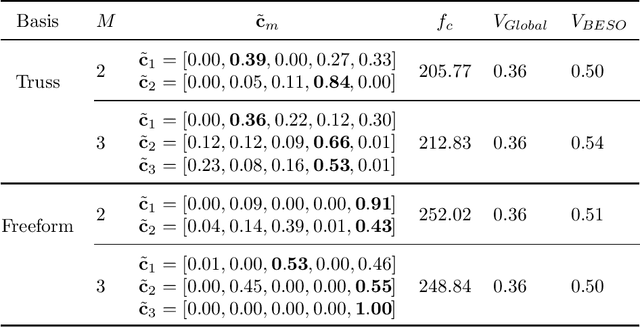
To create heterogeneous, multiscale structures with unprecedented functionalities, recent topology optimization approaches design either fully aperiodic systems or functionally graded structures, which compete in terms of design freedom and efficiency. We propose to inherit the advantages of both through a data-driven framework for multiclass functionally graded structures that mixes several families, i.e., classes, of microstructure topologies to create spatially-varying designs with guaranteed feasibility. The key is a new multiclass shape blending scheme that generates smoothly graded microstructures without requiring compatible classes or connectivity and feasibility constraints. Moreover, it transforms the microscale problem into an efficient, low-dimensional one without confining the design to predefined shapes. Compliance and shape matching examples using common truss geometries and diversity-based freeform topologies demonstrate the versatility of our framework, while studies on the effect of the number and diversity of classes illustrate the effectiveness. The generality of the proposed methods supports future extensions beyond the linear applications presented.

Data-Driven Multiscale Design of Cellular Composites with Multiclass Microstructures for Natural Frequency Maximization

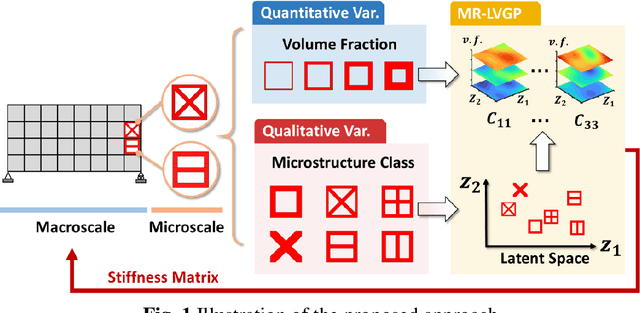
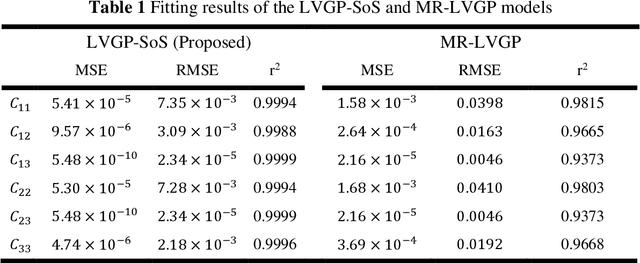
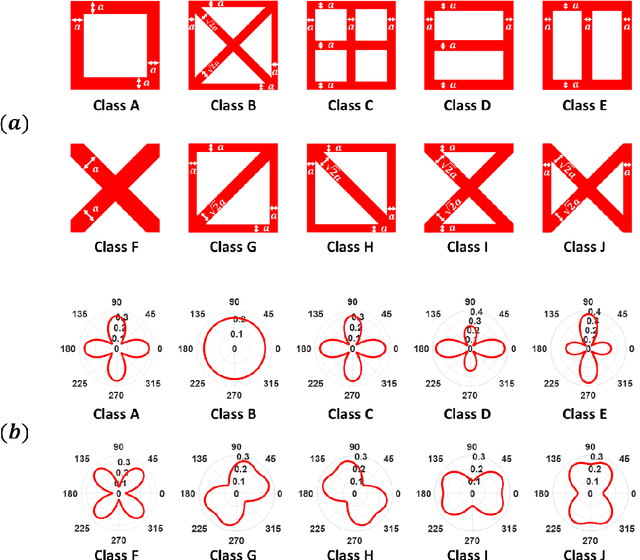
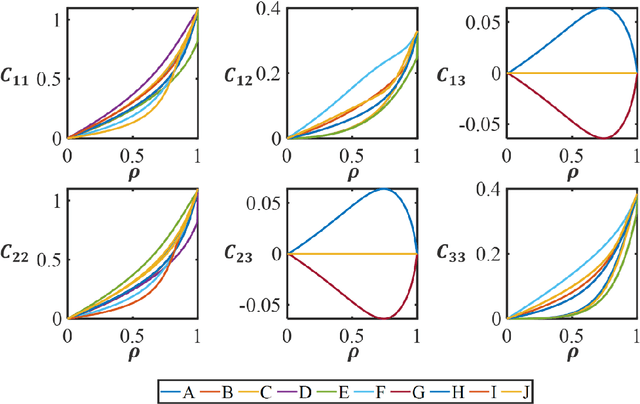
For natural frequency optimization of engineering structures, cellular composites have been shown to possess an edge over solid. However, existing multiscale design methods for cellular composites are either computationally exhaustive or confined to a single class of microstructures. In this paper, we propose a data-driven topology optimization (TO) approach to enable the multiscale design of cellular structures with various choices of microstructure classes. The key component is a newly proposed latent-variable Gaussian process (LVGP) model through which different classes of microstructures are mapped into a low-dimensional continuous latent space. It provides an interpretable distance metric between classes and captures their effects on the homogenized stiffness tensors. By introducing latent vectors as design variables, a differentiable transition of stiffness matrix between classes can be easily achieved with an analytical gradient. After integrating LVGP with the density-based TO, an efficient data-driven cellular composite optimization process is developed to enable concurrent exploration of microstructure concepts and the associated volume fractions for natural frequency optimization. Examples reveal that the proposed cellular designs with multiclass microstructures achieve higher natural frequencies than both single-scale and single-class designs. This framework can be easily extended to other multi-scale TO problems, such as thermal compliance and dynamic response optimization.