T-METASET: Task-Aware Generation of Metamaterial Datasets by Diversity-Based Active Learning

Inspired by the recent success of deep learning in diverse domains, data-driven metamaterials design has emerged as a compelling design paradigm to unlock the potential of multiscale architecture. However, existing model-centric approaches lack principled methodologies dedicated to high-quality data generation. Resorting to space-filling design in shape descriptor space, existing metamaterial datasets suffer from property distributions that are either highly imbalanced or at odds with design tasks of interest. To this end, we propose t-METASET: an intelligent data acquisition framework for task-aware dataset generation. We seek a solution to a commonplace yet frequently overlooked scenario at early design stages: when a massive ($~\sim O(10^4)$) shape library has been prepared with no properties evaluated. The key idea is to exploit a data-driven shape descriptor learned from generative models, fit a sparse regressor as the start-up agent, and leverage diversity-related metrics to drive data acquisition to areas that help designers fulfill design goals. We validate the proposed framework in three hypothetical deployment scenarios, which encompass general use, task-aware use, and tailorable use. Two large-scale shape-only mechanical metamaterial datasets are used as test datasets. The results demonstrate that t-METASET can incrementally grow task-aware datasets. Applicable to general design representations, t-METASET can boost future advancements of not only metamaterials but data-driven design in other domains.

Data-Driven Multiscale Design of Cellular Composites with Multiclass Microstructures for Natural Frequency Maximization

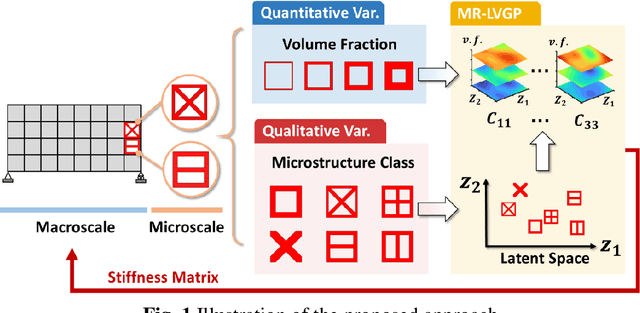
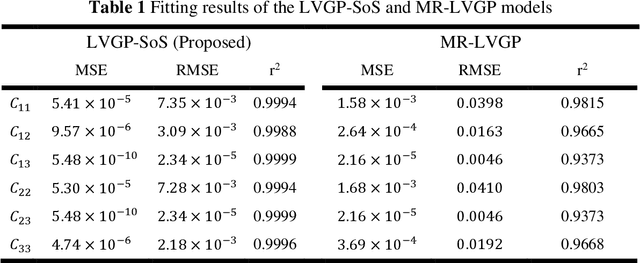
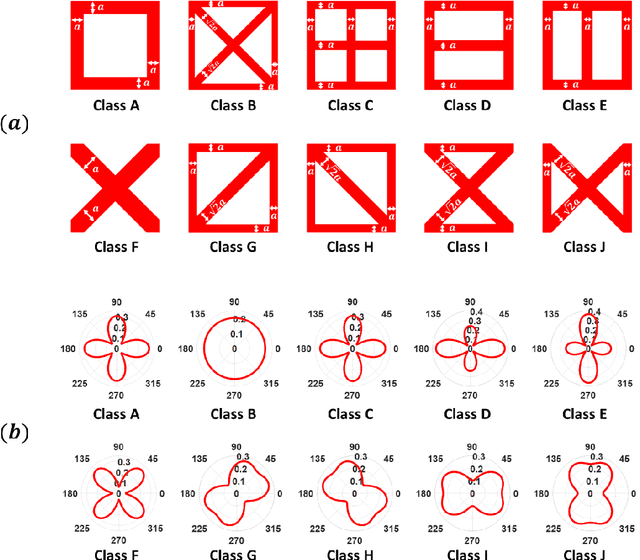
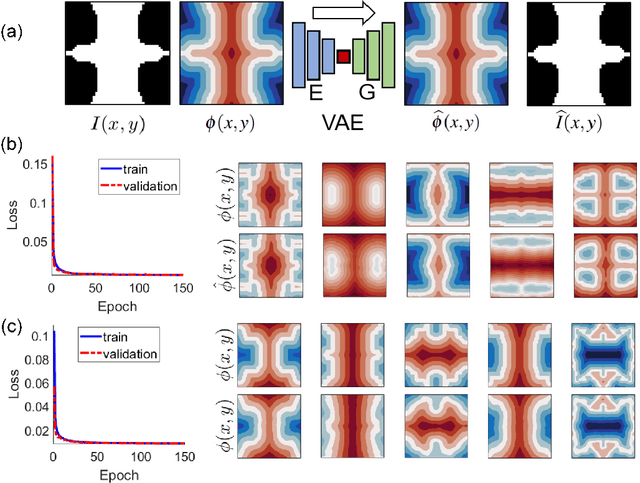
For natural frequency optimization of engineering structures, cellular composites have been shown to possess an edge over solid. However, existing multiscale design methods for cellular composites are either computationally exhaustive or confined to a single class of microstructures. In this paper, we propose a data-driven topology optimization (TO) approach to enable the multiscale design of cellular structures with various choices of microstructure classes. The key component is a newly proposed latent-variable Gaussian process (LVGP) model through which different classes of microstructures are mapped into a low-dimensional continuous latent space. It provides an interpretable distance metric between classes and captures their effects on the homogenized stiffness tensors. By introducing latent vectors as design variables, a differentiable transition of stiffness matrix between classes can be easily achieved with an analytical gradient. After integrating LVGP with the density-based TO, an efficient data-driven cellular composite optimization process is developed to enable concurrent exploration of microstructure concepts and the associated volume fractions for natural frequency optimization. Examples reveal that the proposed cellular designs with multiclass microstructures achieve higher natural frequencies than both single-scale and single-class designs. This framework can be easily extended to other multi-scale TO problems, such as thermal compliance and dynamic response optimization.