Data-Driven Multiscale Design of Cellular Composites with Multiclass Microstructures for Natural Frequency Maximization
Paper and Code
Jun 11, 2021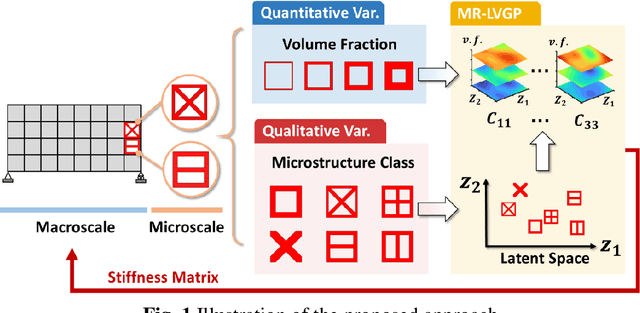
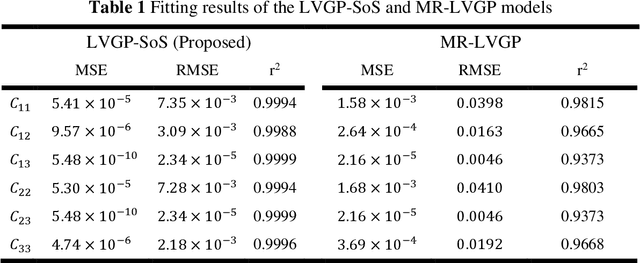
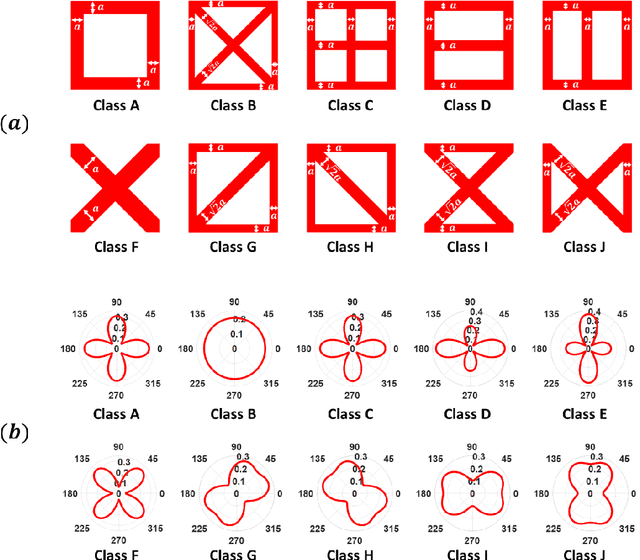
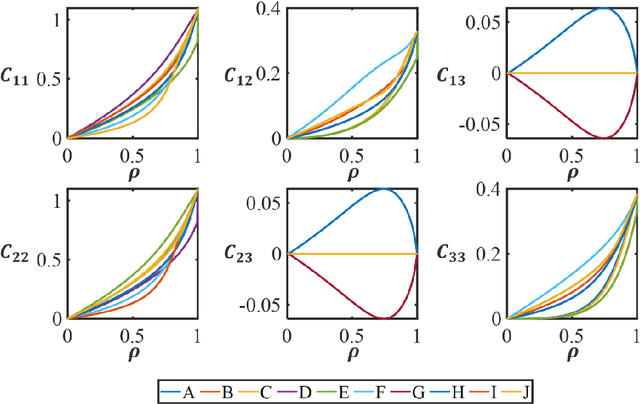
For natural frequency optimization of engineering structures, cellular composites have been shown to possess an edge over solid. However, existing multiscale design methods for cellular composites are either computationally exhaustive or confined to a single class of microstructures. In this paper, we propose a data-driven topology optimization (TO) approach to enable the multiscale design of cellular structures with various choices of microstructure classes. The key component is a newly proposed latent-variable Gaussian process (LVGP) model through which different classes of microstructures are mapped into a low-dimensional continuous latent space. It provides an interpretable distance metric between classes and captures their effects on the homogenized stiffness tensors. By introducing latent vectors as design variables, a differentiable transition of stiffness matrix between classes can be easily achieved with an analytical gradient. After integrating LVGP with the density-based TO, an efficient data-driven cellular composite optimization process is developed to enable concurrent exploration of microstructure concepts and the associated volume fractions for natural frequency optimization. Examples reveal that the proposed cellular designs with multiclass microstructures achieve higher natural frequencies than both single-scale and single-class designs. This framework can be easily extended to other multi-scale TO problems, such as thermal compliance and dynamic response optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge