Data-Driven Design for Metamaterials and Multiscale Systems: A Review

Metamaterials are artificial materials designed to exhibit effective material parameters that go beyond those found in nature. Composed of unit cells with rich designability that are assembled into multiscale systems, they hold great promise for realizing next-generation devices with exceptional, often exotic, functionalities. However, the vast design space and intricate structure-property relationships pose significant challenges in their design. A compelling paradigm that could bring the full potential of metamaterials to fruition is emerging: data-driven design. In this review, we provide a holistic overview of this rapidly evolving field, emphasizing the general methodology instead of specific domains and deployment contexts. We organize existing research into data-driven modules, encompassing data acquisition, machine learning-based unit cell design, and data-driven multiscale optimization. We further categorize the approaches within each module based on shared principles, analyze and compare strengths and applicability, explore connections between different modules, and identify open research questions and opportunities.

T-METASET: Task-Aware Generation of Metamaterial Datasets by Diversity-Based Active Learning

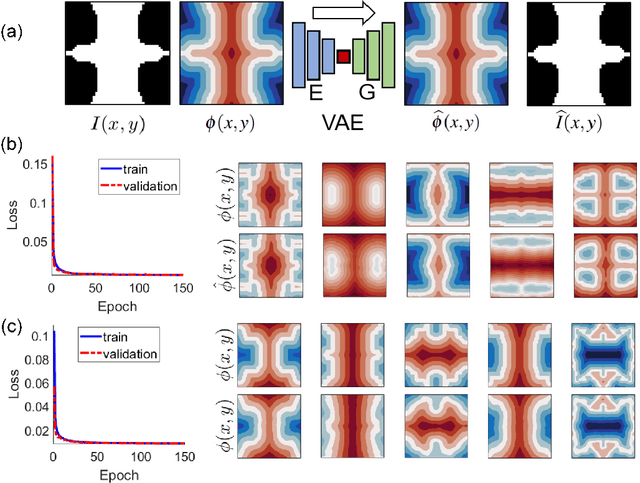
Inspired by the recent success of deep learning in diverse domains, data-driven metamaterials design has emerged as a compelling design paradigm to unlock the potential of multiscale architecture. However, existing model-centric approaches lack principled methodologies dedicated to high-quality data generation. Resorting to space-filling design in shape descriptor space, existing metamaterial datasets suffer from property distributions that are either highly imbalanced or at odds with design tasks of interest. To this end, we propose t-METASET: an intelligent data acquisition framework for task-aware dataset generation. We seek a solution to a commonplace yet frequently overlooked scenario at early design stages: when a massive ($~\sim O(10^4)$) shape library has been prepared with no properties evaluated. The key idea is to exploit a data-driven shape descriptor learned from generative models, fit a sparse regressor as the start-up agent, and leverage diversity-related metrics to drive data acquisition to areas that help designers fulfill design goals. We validate the proposed framework in three hypothetical deployment scenarios, which encompass general use, task-aware use, and tailorable use. Two large-scale shape-only mechanical metamaterial datasets are used as test datasets. The results demonstrate that t-METASET can incrementally grow task-aware datasets. Applicable to general design representations, t-METASET can boost future advancements of not only metamaterials but data-driven design in other domains.

Remixing Functionally Graded Structures: Data-Driven Topology Optimization with Multiclass Shape Blending

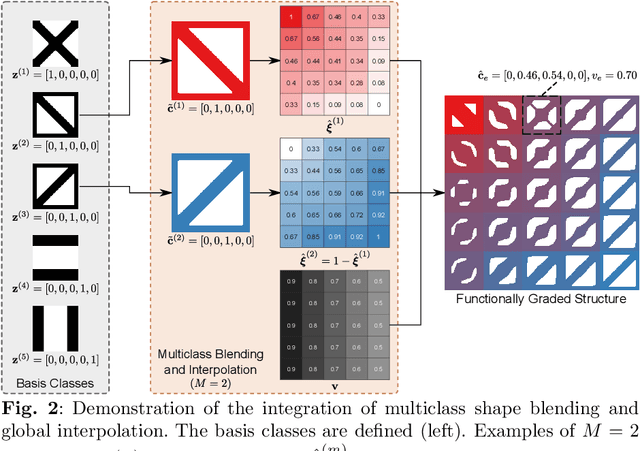
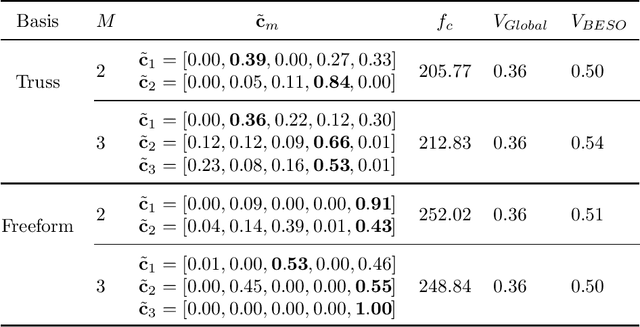
To create heterogeneous, multiscale structures with unprecedented functionalities, recent topology optimization approaches design either fully aperiodic systems or functionally graded structures, which compete in terms of design freedom and efficiency. We propose to inherit the advantages of both through a data-driven framework for multiclass functionally graded structures that mixes several families, i.e., classes, of microstructure topologies to create spatially-varying designs with guaranteed feasibility. The key is a new multiclass shape blending scheme that generates smoothly graded microstructures without requiring compatible classes or connectivity and feasibility constraints. Moreover, it transforms the microscale problem into an efficient, low-dimensional one without confining the design to predefined shapes. Compliance and shape matching examples using common truss geometries and diversity-based freeform topologies demonstrate the versatility of our framework, while studies on the effect of the number and diversity of classes illustrate the effectiveness. The generality of the proposed methods supports future extensions beyond the linear applications presented.

Data-Driven Multiscale Design of Cellular Composites with Multiclass Microstructures for Natural Frequency Maximization

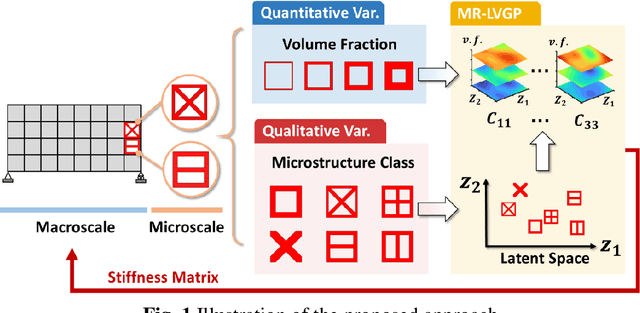
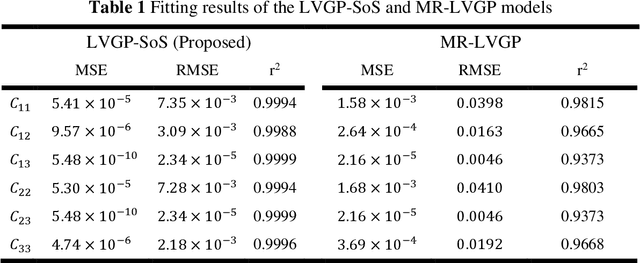
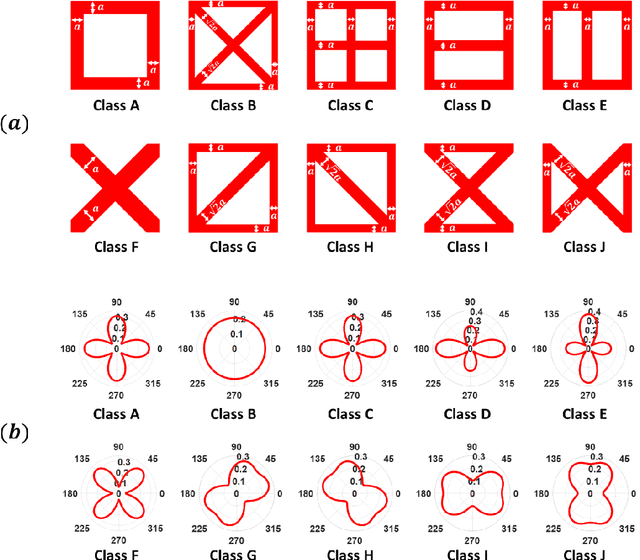
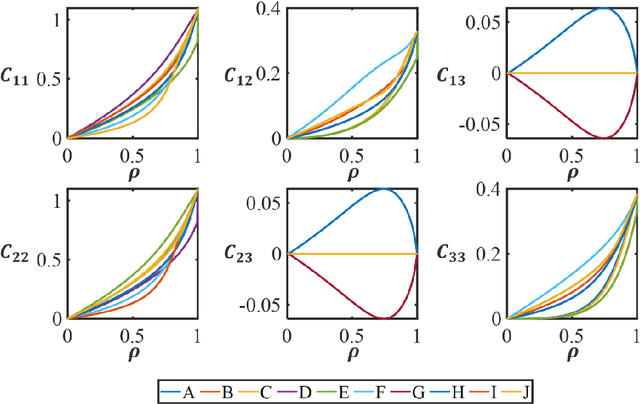
For natural frequency optimization of engineering structures, cellular composites have been shown to possess an edge over solid. However, existing multiscale design methods for cellular composites are either computationally exhaustive or confined to a single class of microstructures. In this paper, we propose a data-driven topology optimization (TO) approach to enable the multiscale design of cellular structures with various choices of microstructure classes. The key component is a newly proposed latent-variable Gaussian process (LVGP) model through which different classes of microstructures are mapped into a low-dimensional continuous latent space. It provides an interpretable distance metric between classes and captures their effects on the homogenized stiffness tensors. By introducing latent vectors as design variables, a differentiable transition of stiffness matrix between classes can be easily achieved with an analytical gradient. After integrating LVGP with the density-based TO, an efficient data-driven cellular composite optimization process is developed to enable concurrent exploration of microstructure concepts and the associated volume fractions for natural frequency optimization. Examples reveal that the proposed cellular designs with multiclass microstructures achieve higher natural frequencies than both single-scale and single-class designs. This framework can be easily extended to other multi-scale TO problems, such as thermal compliance and dynamic response optimization.

Deep Generative Modeling for Mechanistic-based Learning and Design of Metamaterial Systems

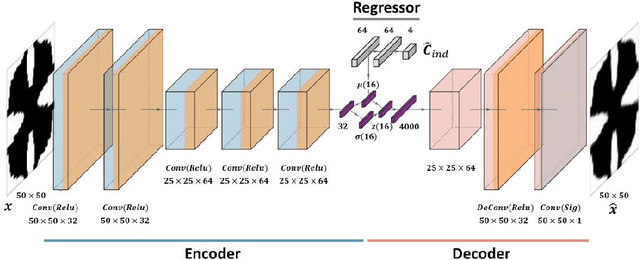
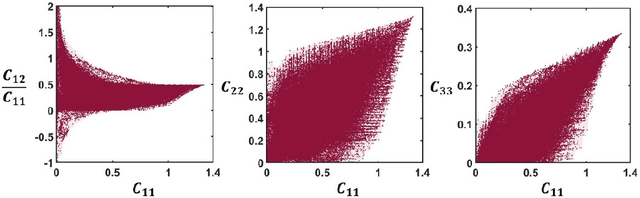
The inverse design of metamaterials is difficult due to a high-dimensional topological design space and presence of multiple local optima. Computational cost is even more demanding for design of multiscale metamaterial systems with aperiodic microstructures and spatially-varying or functionally gradient properties. Despite the growing interest in applying data-driven methods to address this hurdle, current methods either only focus on microstructure generation or adopt an unscalable framework for the multiscale design. In this study, we propose a novel data-driven metamaterial design framework based on deep generative modeling. A deep neural network model consisting of a variational autoencoder (VAE) and a regressor for property prediction is trained on a large metamaterial database to map complex microstructures into a low-dimensional, continuous and organized latent space. Our study shows several advantages of the VAE based generative model. First, the latent space of VAE provides a distance metric to measure shape similarity, enabling interpolation between microstructures and encoding meaningful patterns of variation in geometries and properties. For microstructure design, the tuning of mechanical properties and complex manipulations of microstructures are easily achieved by simple vector operations in the latent space. Second, the vector operation can be further extended to form metamaterial families with controlled gradation of mechanical properties. Third, for multiscale metamaterial systems design, a diverse set of microstructures can be rapidly generated based on target properties at different locations and then assembled by an efficient graph-based optimization method to ensure compatibility between adjacent microstructures. We demonstrate our framework by designing both functionally graded and heterogeneous metamaterial systems that achieve desired distortion behaviors.

METASET: Exploring Shape and Property Spaces for Data-Driven Metamaterials Design

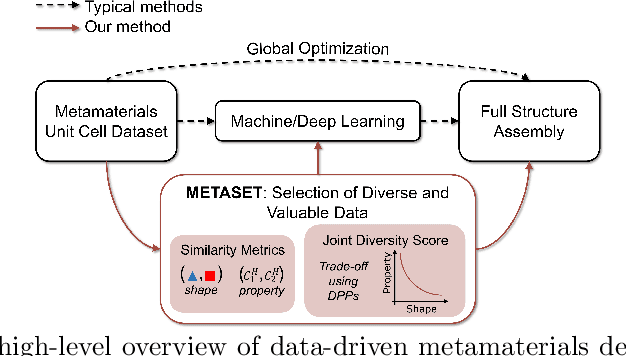
Data-driven design of mechanical metamaterials is an increasingly popular method to combat costly physical simulations and immense, often intractable, geometrical design spaces. Using a precomputed dataset of unit cells, a multiscale structure can be quickly filled via combinatorial search algorithms, and machine learning models can be trained to accelerate the process. However, the dependence on data induces a unique challenge: An imbalanced dataset containing more of certain shapes or physical properties than others can be detrimental to the efficacy of the approaches and any models built on those sets. In answer, we posit that a smaller yet diverse set of unit cells leads to scalable search and unbiased learning. To select such subsets, we propose METASET, a methodology that 1) uses similarity metrics and positive semi-definite kernels to jointly measure the closeness of unit cells in both shape and property spaces, and 2) incorporates Determinantal Point Processes for efficient subset selection. Moreover, METASET allows the trade-off between shape and property diversity so that subsets can be tuned for various applications. Through the design of 2D metamaterials with target displacement profiles, we demonstrate that smaller, diverse subsets can indeed improve the search process as well as structural performance. We also apply METASET to eliminate inherent overlaps in a dataset of 3D unit cells created with symmetry rules, distilling it down to the most unique families. Our diverse subsets are provided publicly for use by any designer.