Bayesian machine learning for Boltzmann machine in quantum-enhanced feature spaces

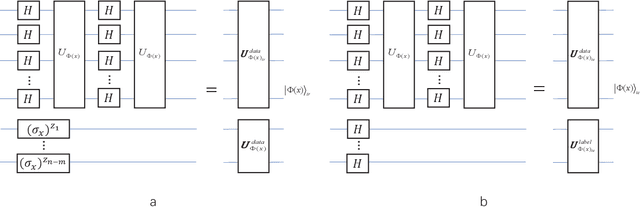
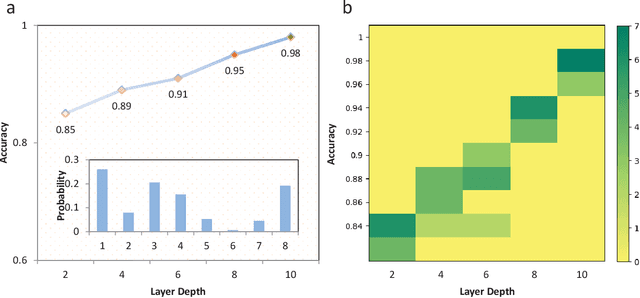
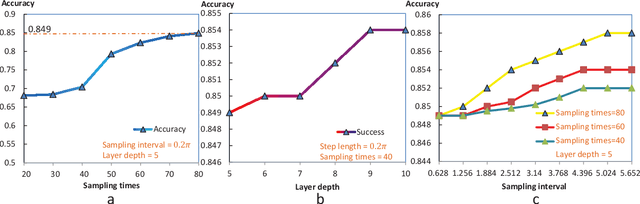
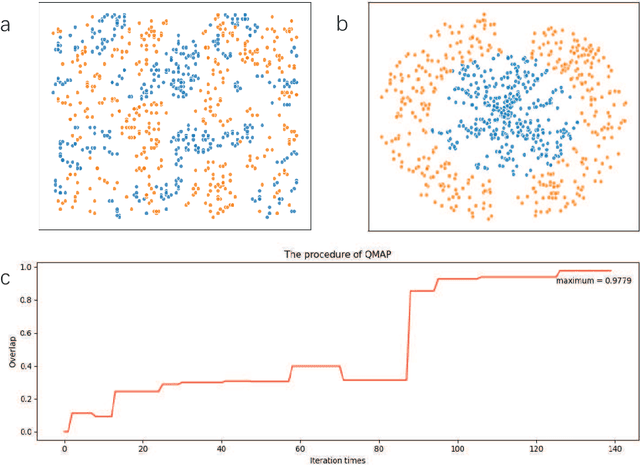
Bayesian learning is ubiquitous for implementing classification and regression tasks, however, it is accompanied by computationally intractable limitations when the feature spaces become extremely large. Aiming to solve this problem, we develop a quantum bayesian learning framework of the restricted Boltzmann machine in the quantum-enhanced feature spaces. Our framework provides the encoding phase to map the real data and Boltzmann weight onto the quantum feature spaces and the training phase to learn an optimal inference function. Specifically, the training phase provides a physical quantity to measure the posterior distribution in quantum feature spaces, and this measure is utilized to design the quantum maximum a posterior (QMAP) algorithm and the quantum predictive distribution estimator (QPDE). It is shown that both quantum algorithms achieve exponential speed-up over their classical counterparts. Furthermore, it is interesting to note that our framework can figure out the classical bayesian learning tasks, i.e. processing the classical data and outputting corresponding classical labels. And a simulation, which is performed on an open-source software framework for quantum computing, illustrates that our algorithms show almost the same classification performance compared to their classical counterparts. Noting that the proposed quantum algorithms utilize the shallow circuit, our work is expected to be implemented on the noisy intermediate-scale quantum (NISQ) devices, and is one of the promising candidates to achieve quantum supremacy.

Operations on soft sets revisited

Soft sets, as a mathematical tool for dealing with uncertainty, have recently gained considerable attention, including some successful applications in information processing, decision, demand analysis, and forecasting. To construct new soft sets from given soft sets, some operations on soft sets have been proposed. Unfortunately, such operations cannot keep all classical set-theoretic laws true for soft sets. In this paper, we redefine the intersection, complement, and difference of soft sets and investigate the algebraic properties of these operations along with a known union operation. We find that the new operation system on soft sets inherits all basic properties of operations on classical sets, which justifies our definitions.

Information-theoretic measures associated with rough set approximations

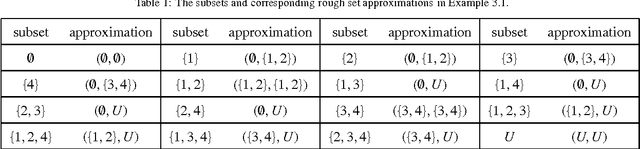
Although some information-theoretic measures of uncertainty or granularity have been proposed in rough set theory, these measures are only dependent on the underlying partition and the cardinality of the universe, independent of the lower and upper approximations. It seems somewhat unreasonable since the basic idea of rough set theory aims at describing vague concepts by the lower and upper approximations. In this paper, we thus define new information-theoretic entropy and co-entropy functions associated to the partition and the approximations to measure the uncertainty and granularity of an approximation space. After introducing the novel notions of entropy and co-entropy, we then examine their properties. In particular, we discuss the relationship of co-entropies between different universes. The theoretical development is accompanied by illustrative numerical examples.

A note on communicating between information systems based on including degrees

In order to study the communication between information systems, Gong and Xiao [Z. Gong and Z. Xiao, Communicating between information systems based on including degrees, International Journal of General Systems 39 (2010) 189--206] proposed the concept of general relation mappings based on including degrees. Some properties and the extension for fuzzy information systems of the general relation mappings have been investigated there. In this paper, we point out by counterexamples that several assertions (Lemma 3.1, Lemma 3.2, Theorem 4.1, and Theorem 4.3) in the aforementioned work are not true in general.

Some improved results on communication between information systems

To study the communication between information systems, Wang et al. [C. Wang, C. Wu, D. Chen, Q. Hu, and C. Wu, Communicating between information systems, Information Sciences 178 (2008) 3228-3239] proposed two concepts of type-1 and type-2 consistent functions. Some properties of such functions and induced relation mappings have been investigated there. In this paper, we provide an improvement of the aforementioned work by disclosing the symmetric relationship between type-1 and type-2 consistent functions. We present more properties of consistent functions and induced relation mappings and improve upon several deficient assertions in the original work. In particular, we unify and extend type-1 and type-2 consistent functions into the so-called neighborhood-consistent functions. This provides a convenient means for studying the communication between information systems based on various neighborhoods.

Homomorphisms between fuzzy information systems revisited

Recently, Wang et al. discussed the properties of fuzzy information systems under homomorphisms in the paper [C. Wang, D. Chen, L. Zhu, Homomorphisms between fuzzy information systems, Applied Mathematics Letters 22 (2009) 1045-1050], where homomorphisms are based upon the concepts of consistent functions and fuzzy relation mappings. In this paper, we classify consistent functions as predecessor-consistent and successor-consistent, and then proceed to present more properties of consistent functions. In addition, we improve some characterizations of fuzzy relation mappings provided by Wang et al.