Information-theoretic measures associated with rough set approximations

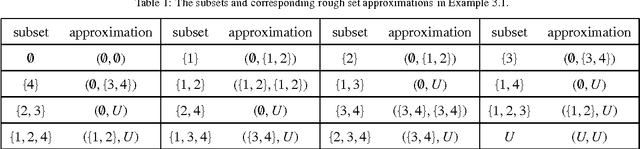
Although some information-theoretic measures of uncertainty or granularity have been proposed in rough set theory, these measures are only dependent on the underlying partition and the cardinality of the universe, independent of the lower and upper approximations. It seems somewhat unreasonable since the basic idea of rough set theory aims at describing vague concepts by the lower and upper approximations. In this paper, we thus define new information-theoretic entropy and co-entropy functions associated to the partition and the approximations to measure the uncertainty and granularity of an approximation space. After introducing the novel notions of entropy and co-entropy, we then examine their properties. In particular, we discuss the relationship of co-entropies between different universes. The theoretical development is accompanied by illustrative numerical examples.