Siyu Tao
ECNU-SenseMaker at SemEval-2020 Task 4: Leveraging Heterogeneous Knowledge Resources for Commonsense Validation and Explanation
Jul 28, 2020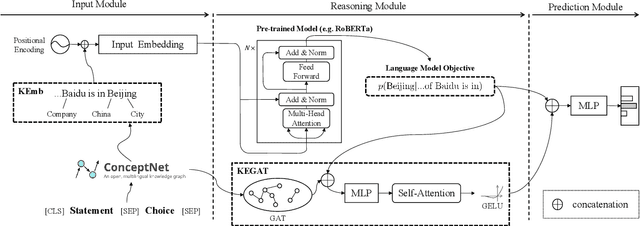

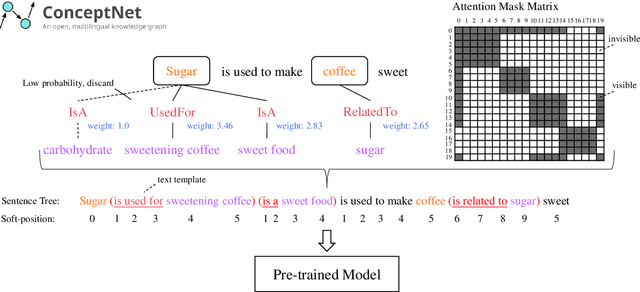
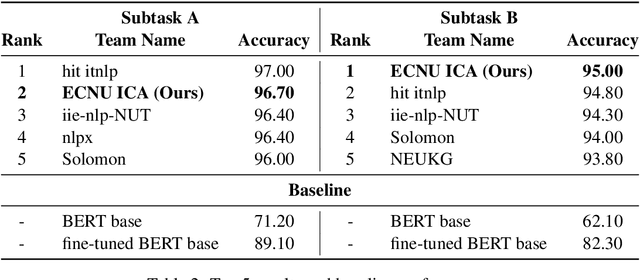
Abstract:This paper describes our system for SemEval-2020 Task 4: Commonsense Validation and Explanation (Wang et al., 2020). We propose a novel Knowledge-enhanced Graph Attention Network (KEGAT) architecture for this task, leveraging heterogeneous knowledge from both the structured knowledge base (i.e. ConceptNet) and unstructured text to better improve the ability of a machine in commonsense understanding. This model has a powerful commonsense inference capability via utilizing suitable commonsense incorporation methods and upgraded data augmentation techniques. Besides, an internal sharing mechanism is cooperated to prohibit our model from insufficient and excessive reasoning for commonsense. As a result, this model performs quite well in both validation and explanation. For instance, it achieves state-of-the-art accuracy in the subtask called Commonsense Explanation (Multi-Choice). We officially name the system as ECNU-SenseMaker. Code is publicly available at https://github.com/ECNU-ICA/ECNU-SenseMaker.
Data-Driven Topology Optimization with Multiclass Microstructures using Latent Variable Gaussian Process
Jun 27, 2020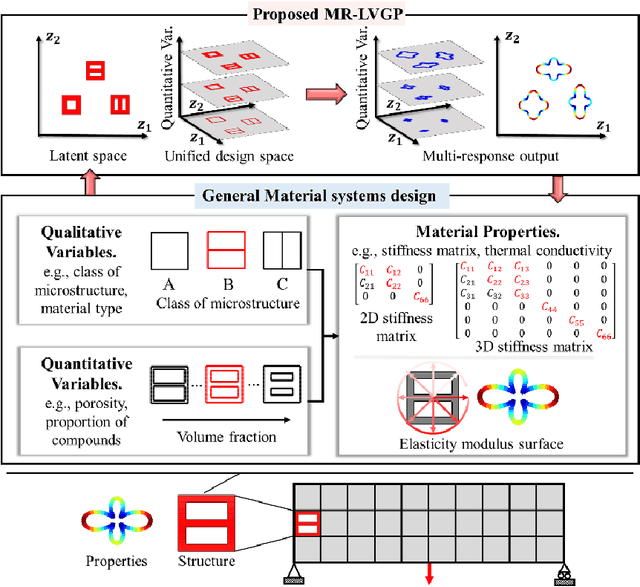
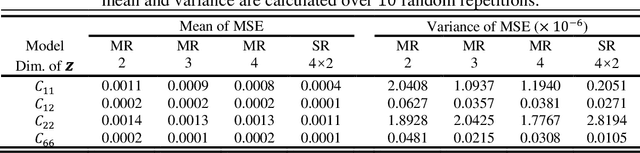
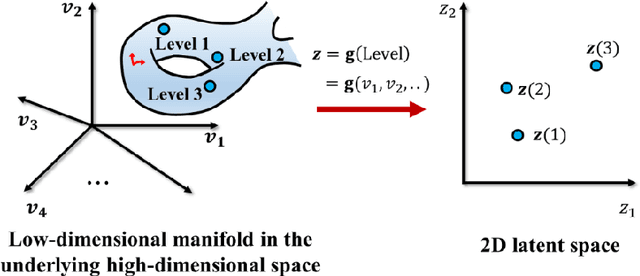
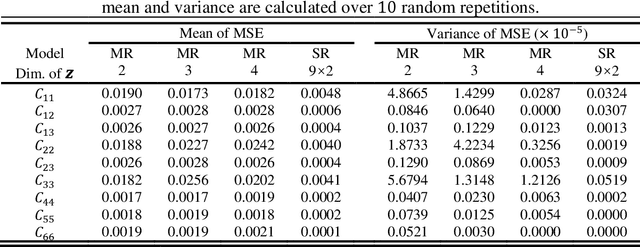
Abstract:The data-driven approach is emerging as a promising method for the topological design of multiscale structures with greater efficiency. However, existing data-driven methods mostly focus on a single class of microstructures without considering multiple classes to accommodate spatially varying desired properties. The key challenge is the lack of an inherent ordering or distance measure between different classes of microstructures in meeting a range of properties. To overcome this hurdle, we extend the newly developed latent-variable Gaussian process (LVGP) models to create multi-response LVGP (MR-LVGP) models for the microstructure libraries of metamaterials, taking both qualitative microstructure concepts and quantitative microstructure design variables as mixed-variable inputs. The MR-LVGP model embeds the mixed variables into a continuous design space based on their collective effects on the responses, providing substantial insights into the interplay between different geometrical classes and material parameters of microstructures. With this model, we can easily obtain a continuous and differentiable transition between different microstructure concepts that can render gradient information for multiscale topology optimization. We demonstrate its benefits through multiscale topology optimization with aperiodic microstructures. Design examples reveal that considering multiclass microstructures can lead to improved performance due to the consistent load-transfer paths for micro- and macro-structures.
Data-Centric Mixed-Variable Bayesian Optimization For Materials Design
Jul 04, 2019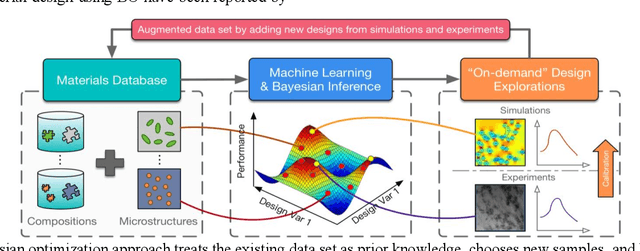

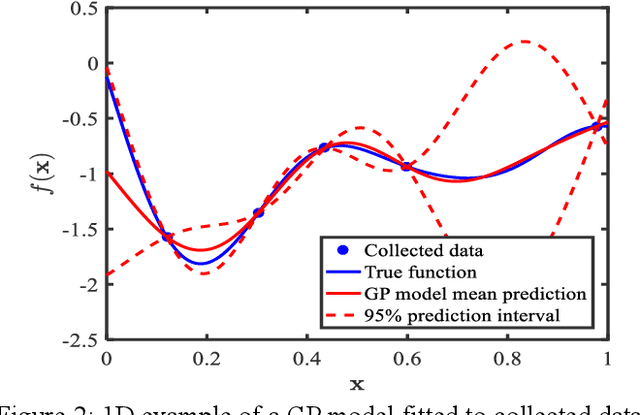
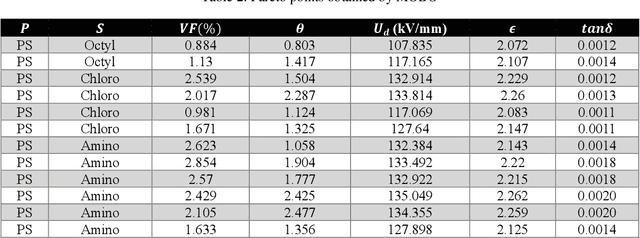
Abstract:Materials design can be cast as an optimization problem with the goal of achieving desired properties, by varying material composition, microstructure morphology, and processing conditions. Existence of both qualitative and quantitative material design variables leads to disjointed regions in property space, making the search for optimal design challenging. Limited availability of experimental data and the high cost of simulations magnify the challenge. This situation calls for design methodologies that can extract useful information from existing data and guide the search for optimal designs efficiently. To this end, we present a data-centric, mixed-variable Bayesian Optimization framework that integrates data from literature, experiments, and simulations for knowledge discovery and computational materials design. Our framework pivots around the Latent Variable Gaussian Process (LVGP), a novel Gaussian Process technique which projects qualitative variables on a continuous latent space for covariance formulation, as the surrogate model to quantify "lack of data" uncertainty. Expected improvement, an acquisition criterion that balances exploration and exploitation, helps navigate a complex, nonlinear design space to locate the optimum design. The proposed framework is tested through a case study which seeks to concurrently identify the optimal composition and morphology for insulating polymer nanocomposites. We also present an extension of mixed-variable Bayesian Optimization for multiple objectives to identify the Pareto Frontier within tens of iterations. These findings project Bayesian Optimization as a powerful tool for design of engineered material systems.
A Latent Variable Approach to Gaussian Process Modeling with Qualitative and Quantitative Factors
Jun 19, 2018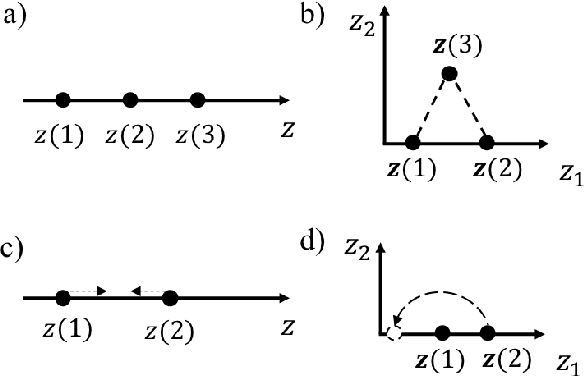


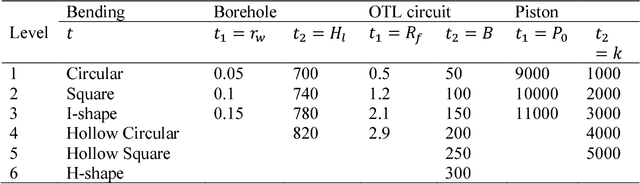
Abstract:Computer simulations often involve both qualitative and numerical inputs. Existing Gaussian process (GP) methods for handling this mainly assume a different response surface for each combination of levels of the qualitative factors and relate them via a multiresponse cross-covariance matrix. We introduce a substantially different approach that maps each qualitative factor to an underlying numerical latent variable (LV), with the mapped value for each level estimated similarly to the covariance lengthscale parameters. This provides a parsimonious GP parameterization that treats qualitative factors the same as numerical variables and views them as effecting the response via similar physical mechanisms. This has strong physical justification, as the effects of a qualitative factor in any physics-based simulation model must always be due to some underlying numerical variables. Even when the underlying variables are many, sufficient dimension reduction arguments imply that their effects can be represented by a low-dimensional LV. This conjecture is supported by the superior predictive performance observed across a variety of examples. Moreover, the mapped LVs provide substantial insight into the nature and effects of the qualitative factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge