Interpretable Architecture Neural Networks for Function Visualization

In many scientific research fields, understanding and visualizing a black-box function in terms of the effects of all the input variables is of great importance. Existing visualization tools do not allow one to visualize the effects of all the input variables simultaneously. Although one can select one or two of the input variables to visualize via a 2D or 3D plot while holding other variables fixed, this presents an oversimplified and incomplete picture of the model. To overcome this shortcoming, we present a new visualization approach using an interpretable architecture neural network (IANN) to visualize the effects of all the input variables directly and simultaneously. We propose two interpretable structures, each of which can be conveniently represented by a specific IANN, and we discuss a number of possible extensions. We also provide a Python package to implement our proposed method. The supplemental materials are available online.

Fully Bayesian inference for latent variable Gaussian process models

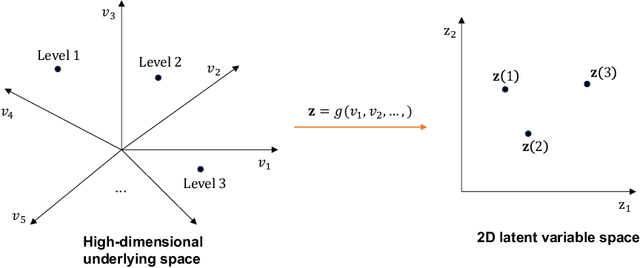
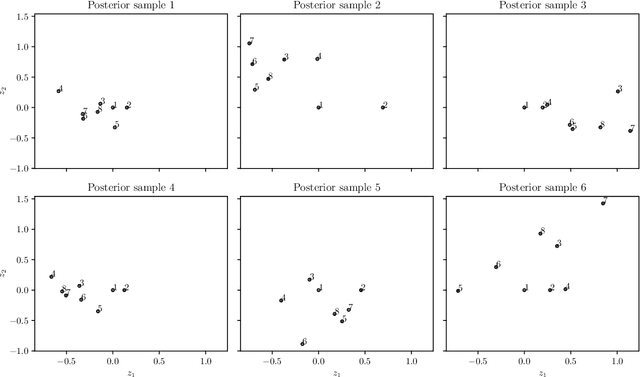
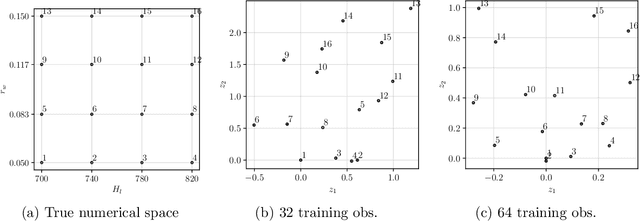
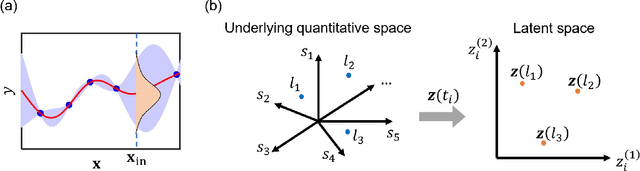
Real engineering and scientific applications often involve one or more qualitative inputs. Standard Gaussian processes (GPs), however, cannot directly accommodate qualitative inputs. The recently introduced latent variable Gaussian process (LVGP) overcomes this issue by first mapping each qualitative factor to underlying latent variables (LVs), and then uses any standard GP covariance function over these LVs. The LVs are estimated similarly to the other GP hyperparameters through maximum likelihood estimation, and then plugged into the prediction expressions. However, this plug-in approach will not account for uncertainty in estimation of the LVs, which can be significant especially with limited training data. In this work, we develop a fully Bayesian approach for the LVGP model and for visualizing the effects of the qualitative inputs via their LVs. We also develop approximations for scaling up LVGPs and fully Bayesian inference for the LVGP hyperparameters. We conduct numerical studies comparing plug-in inference against fully Bayesian inference over a few engineering models and material design applications. In contrast to previous studies on standard GP modeling that have largely concluded that a fully Bayesian treatment offers limited improvements, our results show that for LVGP modeling it offers significant improvements in prediction accuracy and uncertainty quantification over the plug-in approach.

Uncertainty-aware Mixed-variable Machine Learning for Materials Design

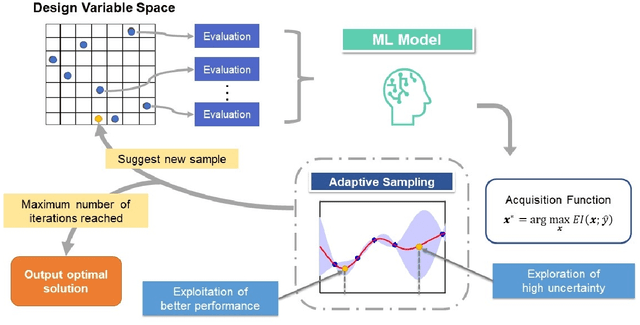
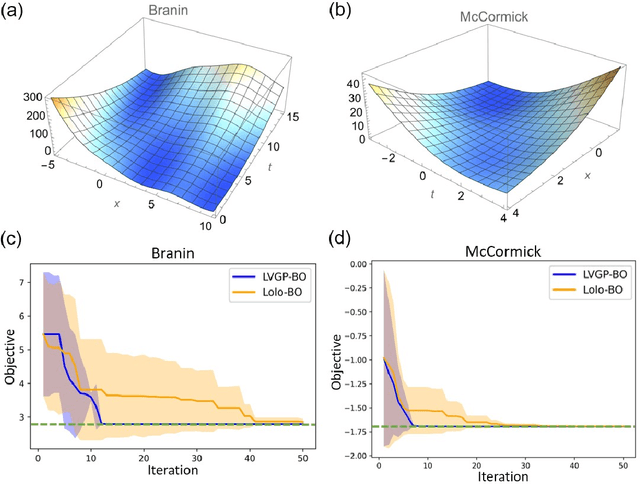
Data-driven design shows the promise of accelerating materials discovery but is challenging due to the prohibitive cost of searching the vast design space of chemistry, structure, and synthesis methods. Bayesian Optimization (BO) employs uncertainty-aware machine learning models to select promising designs to evaluate, hence reducing the cost. However, BO with mixed numerical and categorical variables, which is of particular interest in materials design, has not been well studied. In this work, we survey frequentist and Bayesian approaches to uncertainty quantification of machine learning with mixed variables. We then conduct a systematic comparative study of their performances in BO using a popular representative model from each group, the random forest-based Lolo model (frequentist) and the latent variable Gaussian process model (Bayesian). We examine the efficacy of the two models in the optimization of mathematical functions, as well as properties of structural and functional materials, where we observe performance differences as related to problem dimensionality and complexity. By investigating the machine learning models' predictive and uncertainty estimation capabilities, we provide interpretations of the observed performance differences. Our results provide practical guidance on choosing between frequentist and Bayesian uncertainty-aware machine learning models for mixed-variable BO in materials design.

Concept Drift Monitoring and Diagnostics of Supervised Learning Models via Score Vectors

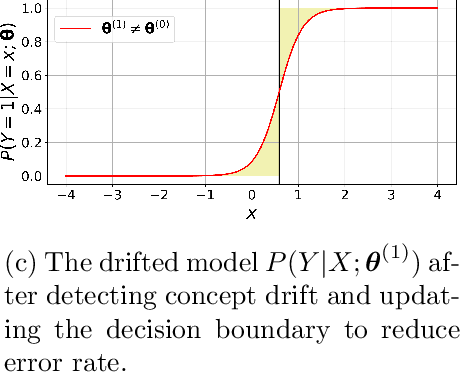
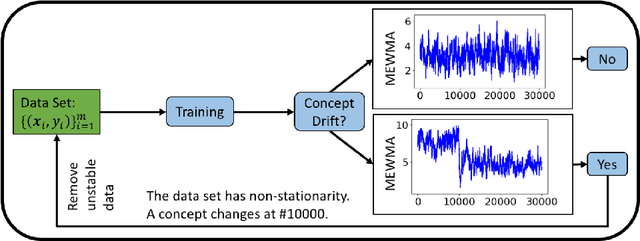
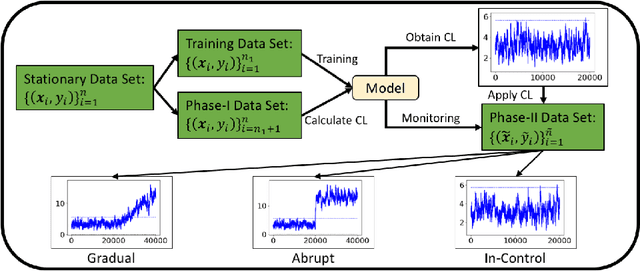
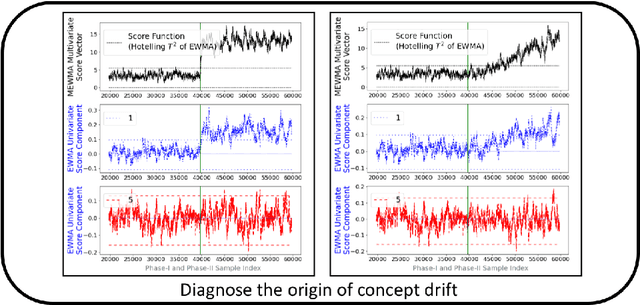
Supervised learning models are one of the most fundamental classes of models. Viewing supervised learning from a probabilistic perspective, the set of training data to which the model is fitted is usually assumed to follow a stationary distribution. However, this stationarity assumption is often violated in a phenomenon called concept drift, which refers to changes over time in the predictive relationship between covariates $\mathbf{X}$ and a response variable $Y$ and can render trained models suboptimal or obsolete. We develop a comprehensive and computationally efficient framework for detecting, monitoring, and diagnosing concept drift. Specifically, we monitor the Fisher score vector, defined as the gradient of the log-likelihood for the fitted model, using a form of multivariate exponentially weighted moving average, which monitors for general changes in the mean of a random vector. In spite of the substantial performance advantages that we demonstrate over popular error-based methods, a score-based approach has not been previously considered for concept drift monitoring. Advantages of the proposed score-based framework include applicability to any parametric model, more powerful detection of changes as shown in theory and experiments, and inherent diagnostic capabilities for helping to identify the nature of the changes.

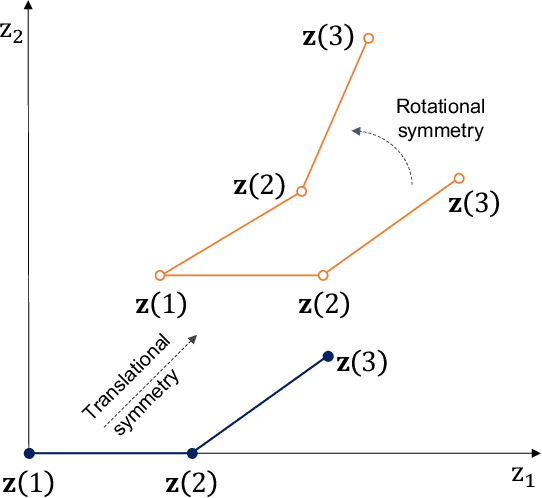
A Latent Variable Approach to Gaussian Process Modeling with Qualitative and Quantitative Factors

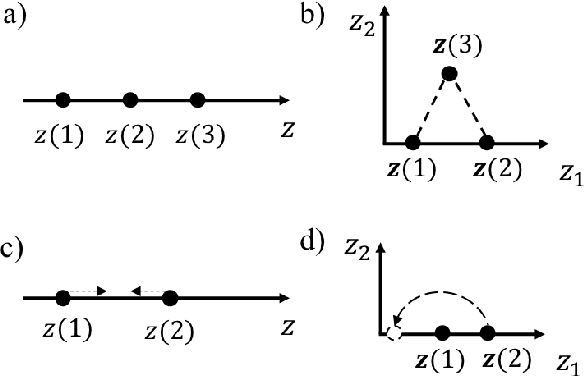
Computer simulations often involve both qualitative and numerical inputs. Existing Gaussian process (GP) methods for handling this mainly assume a different response surface for each combination of levels of the qualitative factors and relate them via a multiresponse cross-covariance matrix. We introduce a substantially different approach that maps each qualitative factor to an underlying numerical latent variable (LV), with the mapped value for each level estimated similarly to the covariance lengthscale parameters. This provides a parsimonious GP parameterization that treats qualitative factors the same as numerical variables and views them as effecting the response via similar physical mechanisms. This has strong physical justification, as the effects of a qualitative factor in any physics-based simulation model must always be due to some underlying numerical variables. Even when the underlying variables are many, sufficient dimension reduction arguments imply that their effects can be represented by a low-dimensional LV. This conjecture is supported by the superior predictive performance observed across a variety of examples. Moreover, the mapped LVs provide substantial insight into the nature and effects of the qualitative factors.