L. Catherine Brinson
34 Examples of LLM Applications in Materials Science and Chemistry: Towards Automation, Assistants, Agents, and Accelerated Scientific Discovery
May 05, 2025
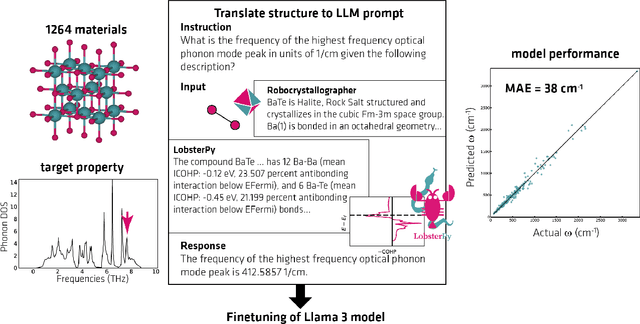
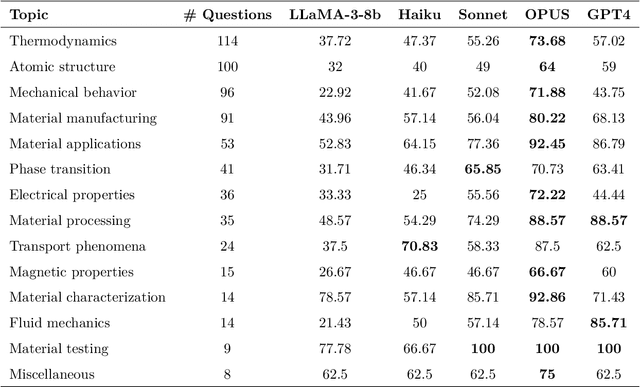
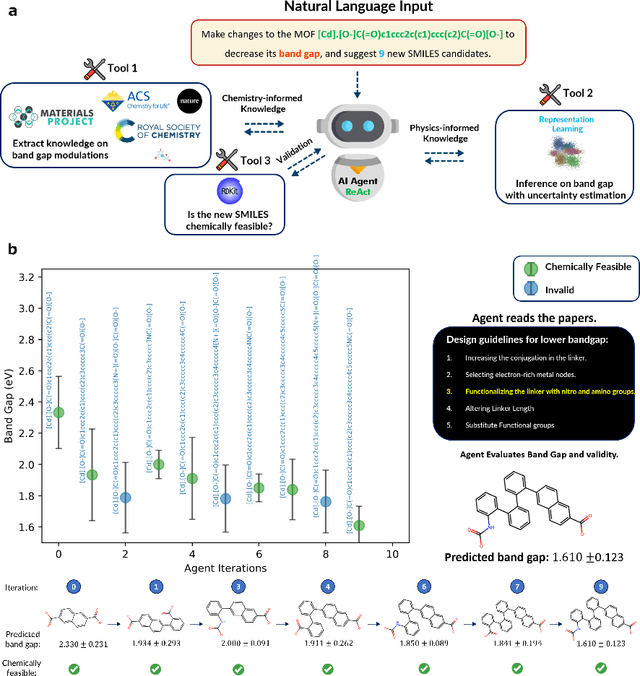
Abstract:Large Language Models (LLMs) are reshaping many aspects of materials science and chemistry research, enabling advances in molecular property prediction, materials design, scientific automation, knowledge extraction, and more. Recent developments demonstrate that the latest class of models are able to integrate structured and unstructured data, assist in hypothesis generation, and streamline research workflows. To explore the frontier of LLM capabilities across the research lifecycle, we review applications of LLMs through 34 total projects developed during the second annual Large Language Model Hackathon for Applications in Materials Science and Chemistry, a global hybrid event. These projects spanned seven key research areas: (1) molecular and material property prediction, (2) molecular and material design, (3) automation and novel interfaces, (4) scientific communication and education, (5) research data management and automation, (6) hypothesis generation and evaluation, and (7) knowledge extraction and reasoning from the scientific literature. Collectively, these applications illustrate how LLMs serve as versatile predictive models, platforms for rapid prototyping of domain-specific tools, and much more. In particular, improvements in both open source and proprietary LLM performance through the addition of reasoning, additional training data, and new techniques have expanded effectiveness, particularly in low-data environments and interdisciplinary research. As LLMs continue to improve, their integration into scientific workflows presents both new opportunities and new challenges, requiring ongoing exploration, continued refinement, and further research to address reliability, interpretability, and reproducibility.
A Framework for Supervised and Unsupervised Segmentation and Classification of Materials Microstructure Images
Feb 10, 2025Abstract:Microstructure of materials is often characterized through image analysis to understand processing-structure-properties linkages. We propose a largely automated framework that integrates unsupervised and supervised learning methods to classify micrographs according to microstructure phase/class and, for multiphase microstructures, segments them into different homogeneous regions. With the advance of manufacturing and imaging techniques, the ultra-high resolution of imaging that reveals the complexity of microstructures and the rapidly increasing quantity of images (i.e., micrographs) enables and necessitates a more powerful and automated framework to extract materials characteristics and knowledge. The framework we propose can be used to gradually build a database of microstructure classes relevant to a particular process or group of materials, which can help in analyzing and discovering/identifying new materials. The framework has three steps: (1) segmentation of multiphase micrographs through a recently developed score-based method so that different microstructure homogeneous regions can be identified in an unsupervised manner; (2) {identification and classification of} homogeneous regions of micrographs through an uncertainty-aware supervised classification network trained using the segmented micrographs from Step $1$ with their identified labels verified via the built-in uncertainty quantification and minimal human inspection; (3) supervised segmentation (more powerful than the segmentation in Step $1$) of multiphase microstructures through a segmentation network trained with micrographs and the results from Steps $1$-$2$ using a form of data augmentation. This framework can iteratively characterize/segment new homogeneous or multiphase materials while expanding the database to enhance performance. The framework is demonstrated on various sets of materials and texture images.
Reflections from the 2024 Large Language Model (LLM) Hackathon for Applications in Materials Science and Chemistry
Nov 20, 2024
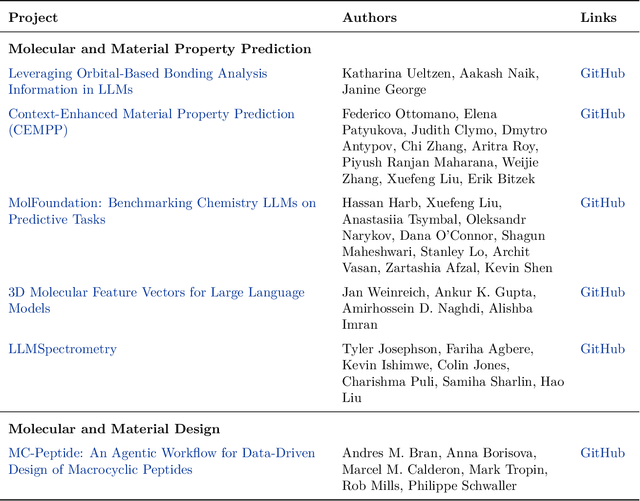
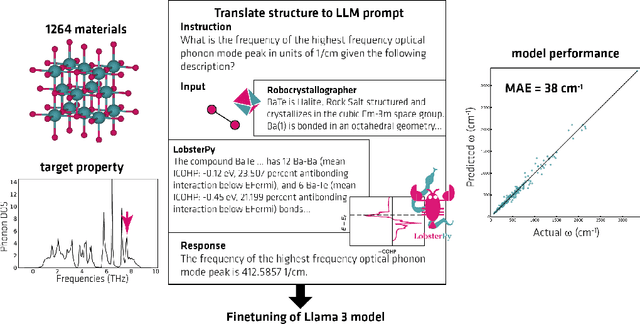
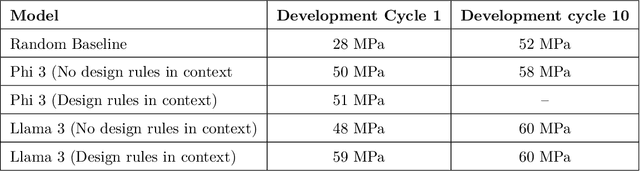
Abstract:Here, we present the outcomes from the second Large Language Model (LLM) Hackathon for Applications in Materials Science and Chemistry, which engaged participants across global hybrid locations, resulting in 34 team submissions. The submissions spanned seven key application areas and demonstrated the diverse utility of LLMs for applications in (1) molecular and material property prediction; (2) molecular and material design; (3) automation and novel interfaces; (4) scientific communication and education; (5) research data management and automation; (6) hypothesis generation and evaluation; and (7) knowledge extraction and reasoning from scientific literature. Each team submission is presented in a summary table with links to the code and as brief papers in the appendix. Beyond team results, we discuss the hackathon event and its hybrid format, which included physical hubs in Toronto, Montreal, San Francisco, Berlin, Lausanne, and Tokyo, alongside a global online hub to enable local and virtual collaboration. Overall, the event highlighted significant improvements in LLM capabilities since the previous year's hackathon, suggesting continued expansion of LLMs for applications in materials science and chemistry research. These outcomes demonstrate the dual utility of LLMs as both multipurpose models for diverse machine learning tasks and platforms for rapid prototyping custom applications in scientific research.
Phononic materials with effectively scale-separated hierarchical features using interpretable machine learning
Aug 15, 2024Abstract:Manipulating the dispersive characteristics of vibrational waves is beneficial for many applications, e.g., high-precision instruments. architected hierarchical phononic materials have sparked promise tunability of elastodynamic waves and vibrations over multiple frequency ranges. In this article, hierarchical unit-cells are obtained, where features at each length scale result in a band gap within a targeted frequency range. Our novel approach, the ``hierarchical unit-cell template method,'' is an interpretable machine-learning approach that uncovers global unit-cell shape/topology patterns corresponding to predefined band-gap objectives. A scale-separation effect is observed where the coarse-scale band-gap objective is mostly unaffected by the fine-scale features despite the closeness of their length scales, thus enabling an efficient hierarchical algorithm. Moreover, the hierarchical patterns revealed are not predefined or self-similar hierarchies as common in current hierarchical phononic materials. Thus, our approach offers a flexible and efficient method for the exploration of new regions in the hierarchical design space, extracting minimal effective patterns for inverse design in applications targeting multiple frequency ranges.
Uncertainty Quantification of Bandgaps in Acoustic Metamaterials with Stochastic Geometric Defects and Material Properties
Oct 19, 2023Abstract:This paper studies the utility of techniques within uncertainty quantification, namely spectral projection and polynomial chaos expansion, in reducing sampling needs for characterizing acoustic metamaterial dispersion band responses given stochastic material properties and geometric defects. A novel method of encoding geometric defects in an interpretable, resolution independent is showcased in the formation of input space probability distributions. Orders of magnitude sampling reductions down to $\sim10^0$ and $\sim10^1$ are achieved in the 1D and 7D input space scenarios respectively while maintaining accurate output space probability distributions through combining Monte Carlo, quadrature rule, and sparse grid sampling with surrogate model fitting.
14 Examples of How LLMs Can Transform Materials Science and Chemistry: A Reflection on a Large Language Model Hackathon
Jun 13, 2023



Abstract:Chemistry and materials science are complex. Recently, there have been great successes in addressing this complexity using data-driven or computational techniques. Yet, the necessity of input structured in very specific forms and the fact that there is an ever-growing number of tools creates usability and accessibility challenges. Coupled with the reality that much data in these disciplines is unstructured, the effectiveness of these tools is limited. Motivated by recent works that indicated that large language models (LLMs) might help address some of these issues, we organized a hackathon event on the applications of LLMs in chemistry, materials science, and beyond. This article chronicles the projects built as part of this hackathon. Participants employed LLMs for various applications, including predicting properties of molecules and materials, designing novel interfaces for tools, extracting knowledge from unstructured data, and developing new educational applications. The diverse topics and the fact that working prototypes could be generated in less than two days highlight that LLMs will profoundly impact the future of our fields. The rich collection of ideas and projects also indicates that the applications of LLMs are not limited to materials science and chemistry but offer potential benefits to a wide range of scientific disciplines.
How to See Hidden Patterns in Metamaterials with Interpretable Machine Learning
Nov 10, 2021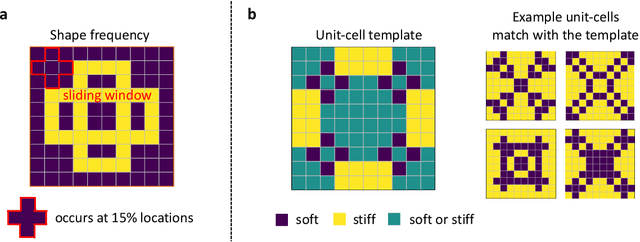

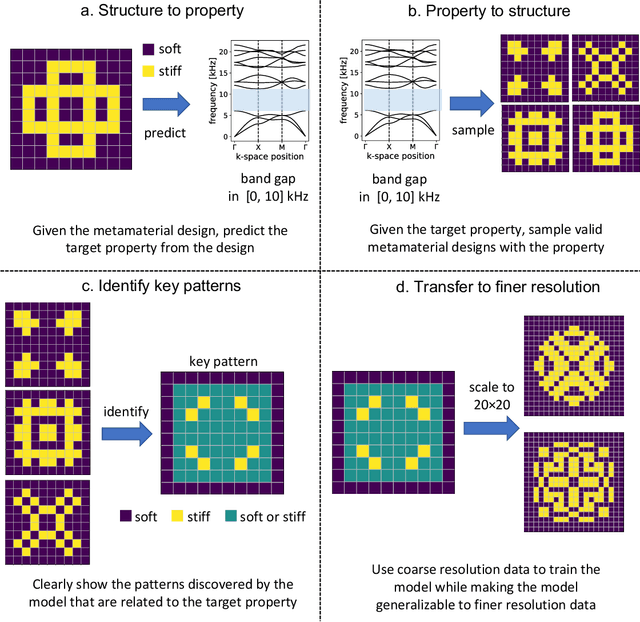

Abstract:Metamaterials are composite materials with engineered geometrical micro- and meso-structures that can lead to uncommon physical properties, like negative Poisson's ratio or ultra-low shear resistance. Periodic metamaterials are composed of repeating unit-cells, and geometrical patterns within these unit-cells influence the propagation of elastic or acoustic waves and control dispersion. In this work, we develop a new interpretable, multi-resolution machine learning framework for finding patterns in the unit-cells of materials that reveal their dynamic properties. Specifically, we propose two new interpretable representations of metamaterials, called shape-frequency features and unit-cell templates. Machine learning models built using these feature classes can accurately predict dynamic material properties. These feature representations (particularly the unit-cell templates) have a useful property: they can operate on designs of higher resolutions. By learning key coarse scale patterns that can be reliably transferred to finer resolution design space via the shape-frequency features or unit-cell templates, we can almost freely design the fine resolution features of the unit-cell without changing coarse scale physics. Through this multi-resolution approach, we are able to design materials that possess target frequency ranges in which waves are allowed or disallowed to propagate (frequency bandgaps). Our approach yields major benefits: (1) unlike typical machine learning approaches to materials science, our models are interpretable, (2) our approaches leverage multi-resolution properties, and (3) our approach provides design flexibility.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge