Kamal Choudhary
AGAPI-Agents: An Open-Access Agentic AI Platform for Accelerated Materials Design on AtomGPT.org
Dec 12, 2025Abstract:Artificial intelligence is reshaping scientific discovery, yet its use in materials research remains limited by fragmented computational ecosystems, reproducibility challenges, and dependence on commercial large language models (LLMs). Here we introduce AGAPI (AtomGPT.org API), an open-access agentic AI platform that integrates more than eight open-source LLMs with over twenty materials-science API endpoints, unifying databases, simulation tools, and machine-learning models through a common orchestration framework. AGAPI employs an Agent-Planner-Executor-Summarizer architecture that autonomously constructs and executes multi-step workflows spanning materials data retrieval, graph neural network property prediction, machine-learning force-field optimization, tight-binding calculations, diffraction analysis, and inverse design. We demonstrate AGAPI through end-to-end workflows, including heterostructure construction, powder X-ray diffraction analysis, and semiconductor defect engineering requiring up to ten sequential operations. In addition, we evaluate AGAPI using 30+ example prompts as test cases and compare agentic predictions with and without tool access against experimental data. With more than 1,000 active users, AGAPI provides a scalable and transparent foundation for reproducible, AI-accelerated materials discovery. AGAPI-Agents codebase is available at https://github.com/atomgptlab/agapi.
A practical guide to machine learning interatomic potentials -- Status and future
Mar 12, 2025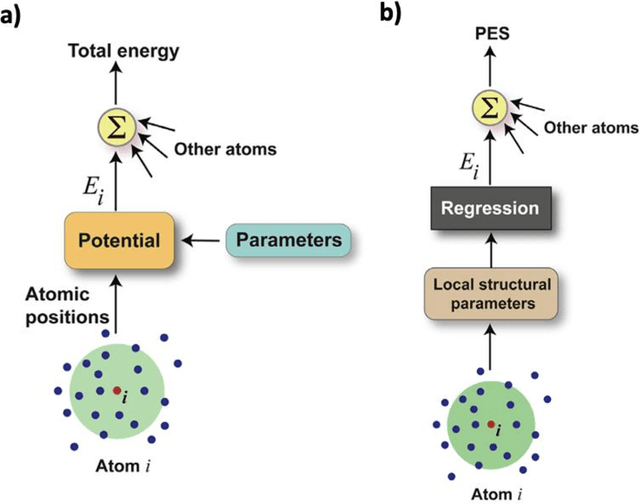

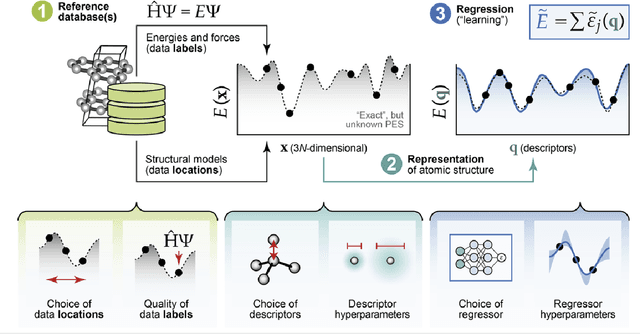
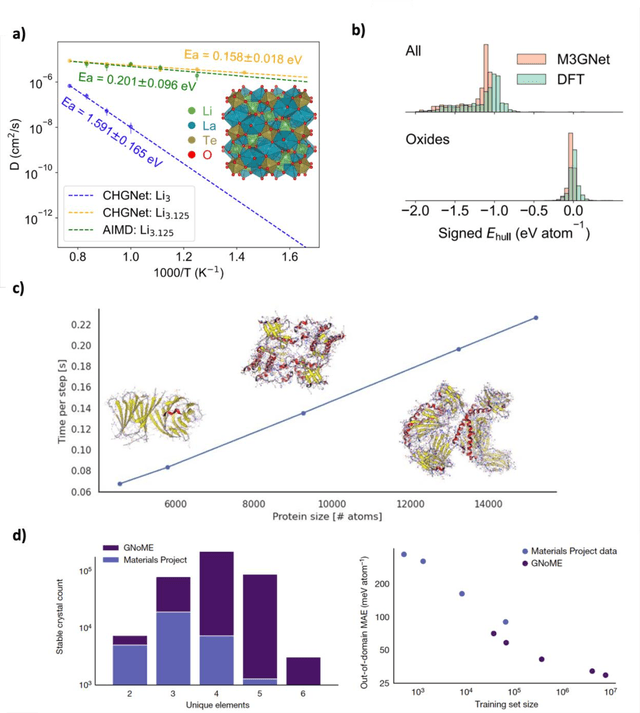
Abstract:The rapid development and large body of literature on machine learning interatomic potentials (MLIPs) can make it difficult to know how to proceed for researchers who are not experts but wish to use these tools. The spirit of this review is to help such researchers by serving as a practical, accessible guide to the state-of-the-art in MLIPs. This review paper covers a broad range of topics related to MLIPs, including (i) central aspects of how and why MLIPs are enablers of many exciting advancements in molecular modeling, (ii) the main underpinnings of different types of MLIPs, including their basic structure and formalism, (iii) the potentially transformative impact of universal MLIPs for both organic and inorganic systems, including an overview of the most recent advances, capabilities, downsides, and potential applications of this nascent class of MLIPs, (iv) a practical guide for estimating and understanding the execution speed of MLIPs, including guidance for users based on hardware availability, type of MLIP used, and prospective simulation size and time, (v) a manual for what MLIP a user should choose for a given application by considering hardware resources, speed requirements, energy and force accuracy requirements, as well as guidance for choosing pre-trained potentials or fitting a new potential from scratch, (vi) discussion around MLIP infrastructure, including sources of training data, pre-trained potentials, and hardware resources for training, (vii) summary of some key limitations of present MLIPs and current approaches to mitigate such limitations, including methods of including long-range interactions, handling magnetic systems, and treatment of excited states, and finally (viii) we finish with some more speculative thoughts on what the future holds for the development and application of MLIPs over the next 3-10+ years.
Approaches for Uncertainty Quantification of AI-predicted Material Properties: A Comparison
Oct 19, 2023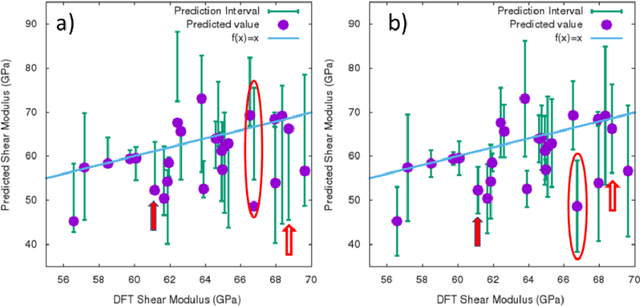


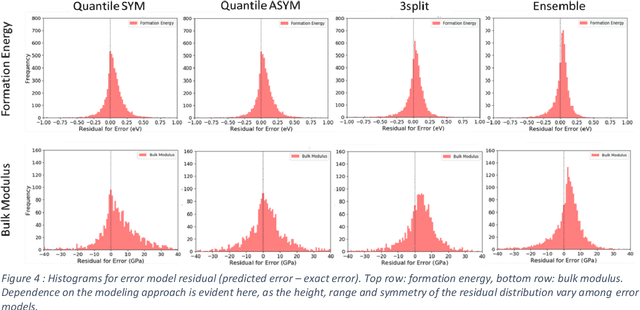
Abstract:The development of large databases of material properties, together with the availability of powerful computers, has allowed machine learning (ML) modeling to become a widely used tool for predicting material performances. While confidence intervals are commonly reported for such ML models, prediction intervals, i.e., the uncertainty on each prediction, are not as frequently available. Here, we investigate three easy-to-implement approaches to determine such individual uncertainty, comparing them across ten ML quantities spanning energetics, mechanical, electronic, optical, and spectral properties. Specifically, we focused on the Quantile approach, the direct machine learning of the prediction intervals and Ensemble methods.
14 Examples of How LLMs Can Transform Materials Science and Chemistry: A Reflection on a Large Language Model Hackathon
Jun 13, 2023



Abstract:Chemistry and materials science are complex. Recently, there have been great successes in addressing this complexity using data-driven or computational techniques. Yet, the necessity of input structured in very specific forms and the fact that there is an ever-growing number of tools creates usability and accessibility challenges. Coupled with the reality that much data in these disciplines is unstructured, the effectiveness of these tools is limited. Motivated by recent works that indicated that large language models (LLMs) might help address some of these issues, we organized a hackathon event on the applications of LLMs in chemistry, materials science, and beyond. This article chronicles the projects built as part of this hackathon. Participants employed LLMs for various applications, including predicting properties of molecules and materials, designing novel interfaces for tools, extracting knowledge from unstructured data, and developing new educational applications. The diverse topics and the fact that working prototypes could be generated in less than two days highlight that LLMs will profoundly impact the future of our fields. The rich collection of ideas and projects also indicates that the applications of LLMs are not limited to materials science and chemistry but offer potential benefits to a wide range of scientific disciplines.
AtomVision: A machine vision library for atomistic images
Dec 05, 2022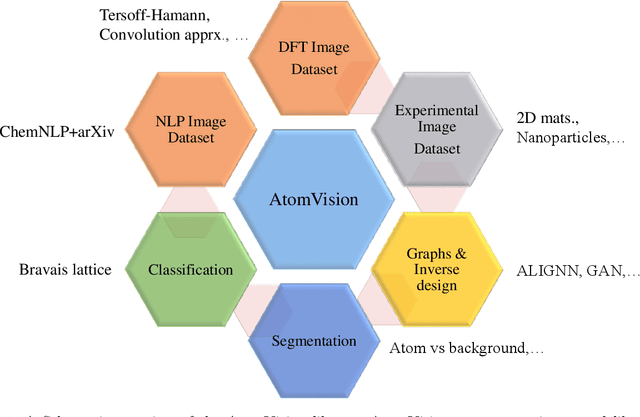
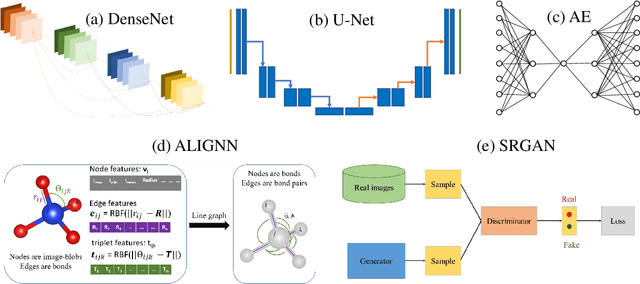
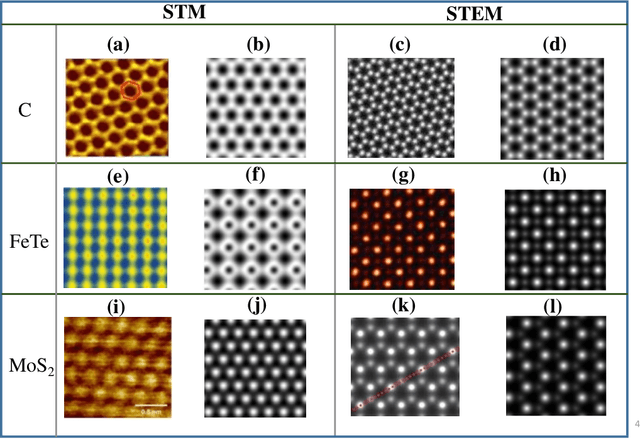
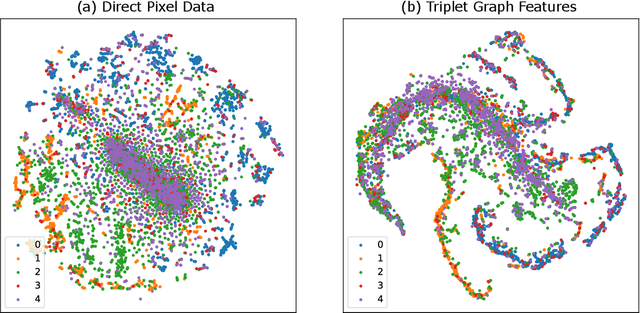
Abstract:Computer vision techniques have immense potential for materials design applications. In this work, we introduce an integrated and general-purpose AtomVision library that can be used to generate, curate scanning tunneling microscopy (STM) and scanning transmission electron microscopy (STEM) datasets and apply machine learning techniques. To demonstrate the applicability of this library, we 1) generate and curate an atomistic image dataset of about 10000 materials, 2) develop and compare convolutional and graph neural network models to classify the Bravais lattices, 3) develop fully convolutional neural network using U-Net architecture to pixelwise classify atom vs background, 4) use generative adversarial network for super-resolution, 5) curate a natural language processing based image dataset using open-access arXiv dataset, and 6) integrate the computational framework with experimental microscopy tools. AtomVision library is available at https://github.com/usnistgov/atomvision.
Prediction of the electron density of states for crystalline compounds with Atomistic Line Graph Neural Networks
Jan 20, 2022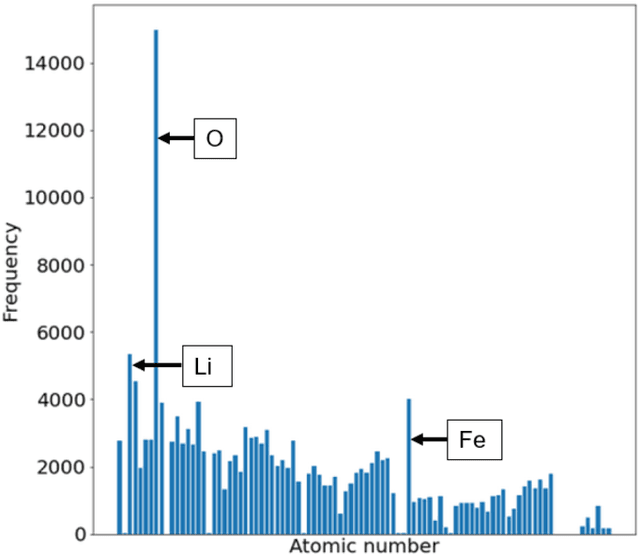
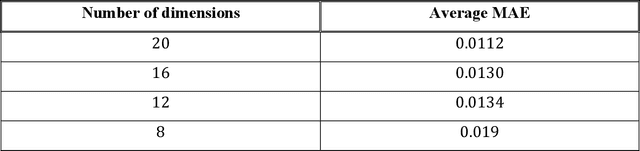
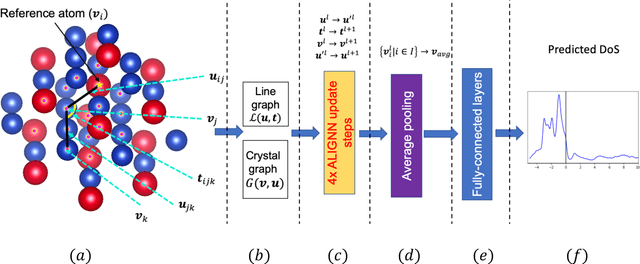
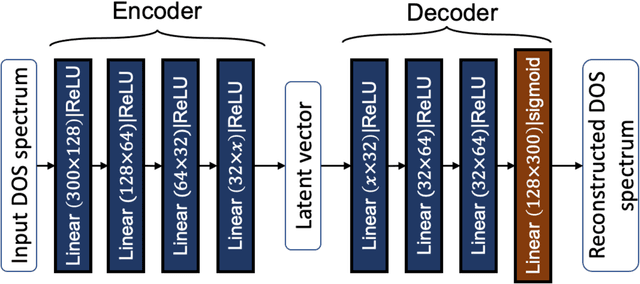
Abstract:Machine learning (ML) based models have greatly enhanced the traditional materials discovery and design pipeline. Specifically, in recent years, surrogate ML models for material property prediction have demonstrated success in predicting discrete scalar-valued target properties to within reasonable accuracy of their DFT-computed values. However, accurate prediction of spectral targets such as the electron Density of States (DOS) poses a much more challenging problem due to the complexity of the target, and the limited amount of available training data. In this study, we present an extension of the recently developed Atomistic Line Graph Neural Network (ALIGNN) to accurately predict DOS of a large set of material unit cell structures, trained to the publicly available JARVIS-DFT dataset. Furthermore, we evaluate two methods of representation of the target quantity - a direct discretized spectrum, and a compressed low-dimensional representation obtained using an autoencoder. Through this work, we demonstrate the utility of graph-based featurization and modeling methods in the prediction of complex targets that depend on both chemistry and directional characteristics of material structures.
Predicting Lattice Phonon Vibrational Frequencies Using Deep Graph Neural Networks
Nov 10, 2021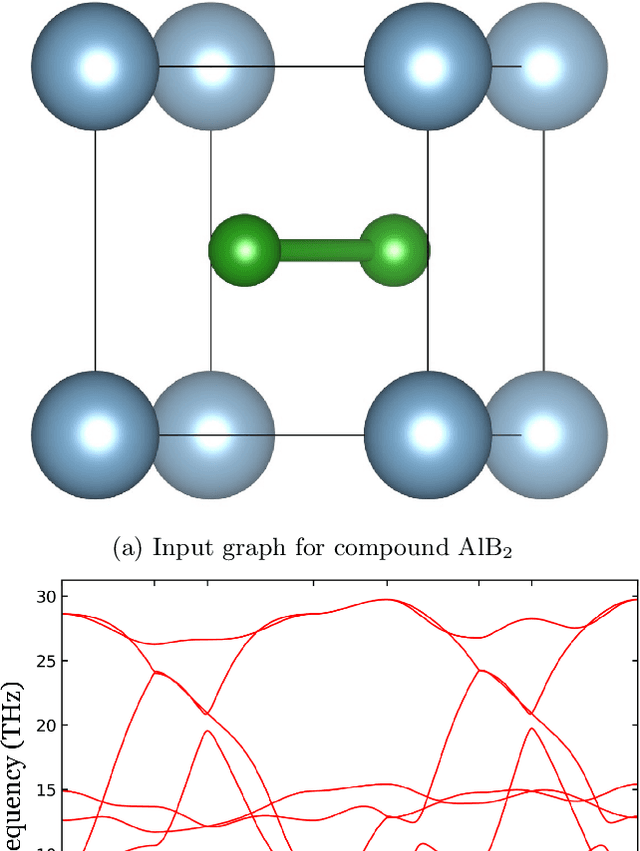
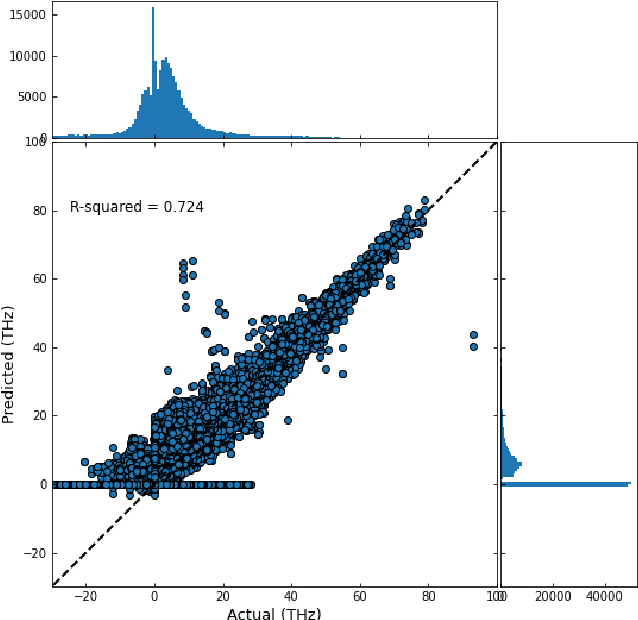
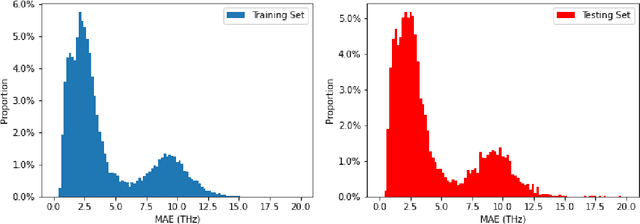
Abstract:Lattice vibration frequencies are related to many important materials properties such as thermal and electrical conductivity as well as superconductivity. However, computational calculation of vibration frequencies using density functional theory (DFT) methods is too computationally demanding for a large number of samples in materials screening. Here we propose a deep graph neural network-based algorithm for predicting crystal vibration frequencies from crystal structures with high accuracy. Our algorithm addresses the variable dimension of vibration frequency spectrum using the zero padding scheme. Benchmark studies on two data sets with 15,000 and 35,552 samples show that the aggregated $R^2$ scores of the prediction reaches 0.554 and 0.724 respectively. Our work demonstrates the capability of deep graph neural networks to learn to predict phonon spectrum properties of crystal structures in addition to phonon density of states (DOS) and electronic DOS in which the output dimension is constant.
Uncertainty Prediction for Machine Learning Models of Material Properties
Jul 16, 2021
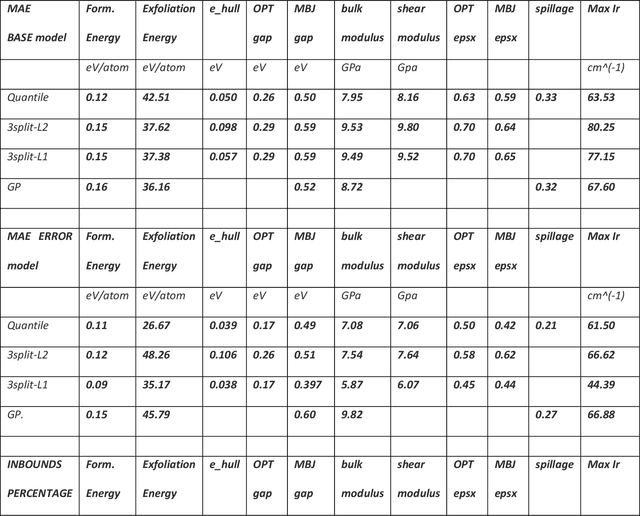


Abstract:Uncertainty quantification in Artificial Intelligence (AI)-based predictions of material properties is of immense importance for the success and reliability of AI applications in material science. While confidence intervals are commonly reported for machine learning (ML) models, prediction intervals, i.e., the evaluation of the uncertainty on each prediction, are seldomly available. In this work we compare 3 different approaches to obtain such individual uncertainty, testing them on 12 ML-physical properties. Specifically, we investigated using the Quantile loss function, machine learning the prediction intervals directly and using Gaussian Processes. We identify each approachs advantages and disadvantages and end up slightly favoring the modeling of the individual uncertainties directly, as it is the easiest to fit and, in most cases, minimizes over-and under-estimation of the predicted errors. All data for training and testing were taken from the publicly available JARVIS-DFT database, and the codes developed for computing the prediction intervals are available through JARVIS-Tools.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge