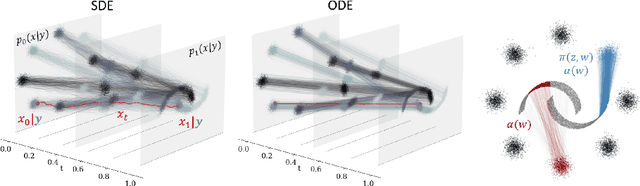
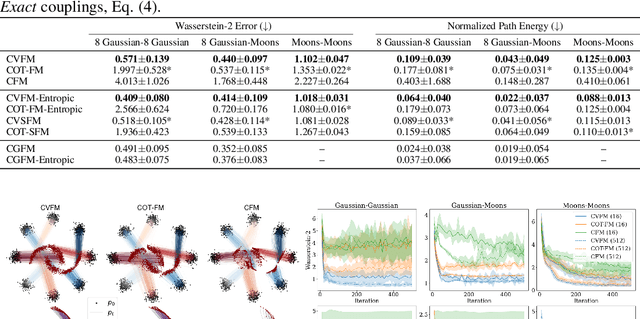
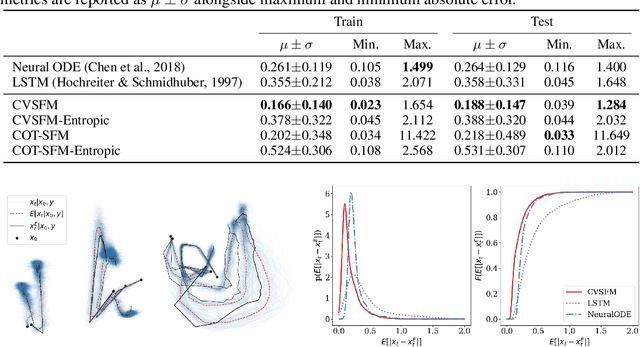
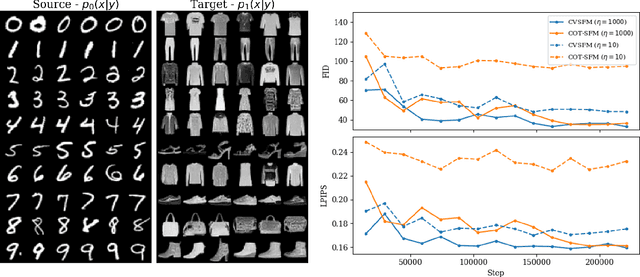
Conditional Variable Flow Matching: Transforming Conditional Densities with Amortized Conditional Optimal Transport

Forecasting stochastic nonlinear dynamical systems under the influence of conditioning variables is a fundamental challenge repeatedly encountered across the biological and physical sciences. While flow-based models can impressively predict the temporal evolution of probability distributions representing possible outcomes of a specific process, existing frameworks cannot satisfactorily account for the impact of conditioning variables on these dynamics. Amongst several limitations, existing methods require training data with paired conditions and are developed for discrete conditioning variables. We propose Conditional Variable Flow Matching (CVFM), a framework for learning flows transforming conditional distributions with amortization across continuous conditioning variables - permitting predictions across the conditional density manifold. This is accomplished through several novel advances, in particular, simultaneous sample conditioned flows over the main and conditioning variables, alongside a conditional Wasserstein distance and kernel facilitating conditional optimal transport. Collectively, these advances allow for learning system dynamics provided measurement data whose states and conditioning variables are not in correspondence. We demonstrate CVFM on a suite of increasingly challenging problems, including discrete and continuous conditional mapping benchmarks, image-to-image domain transfer, and modeling the temporal evolution of materials internal structure during manufacturing processes. We observe that CVFM results in improved performance and convergence characteristics over alternative conditional variants.

Thermodynamically-Informed Iterative Neural Operators for Heterogeneous Elastic Localization

Engineering problems frequently require solution of governing equations with spatially-varying discontinuous coefficients. Even for linear elliptic problems, mapping large ensembles of coefficient fields to solutions can become a major computational bottleneck using traditional numerical solvers. Furthermore, machine learning methods such as neural operators struggle to fit these maps due to sharp transitions and high contrast in the coefficient fields and a scarcity of informative training data. In this work, we focus on a canonical problem in computational mechanics: prediction of local elastic deformation fields over heterogeneous material structures subjected to periodic boundary conditions. We construct a hybrid approximation for the coefficient-to-solution map using a Thermodynamically-informed Iterative Neural Operator (TherINO). Rather than using coefficient fields as direct inputs and iterating over a learned latent space, we employ thermodynamic encodings -- drawn from the constitutive equations -- and iterate over the solution space itself. Through an extensive series of case studies, we elucidate the advantages of these design choices in terms of efficiency, accuracy, and flexibility. We also analyze the model's stability and extrapolation properties on out-of-distribution coefficient fields and demonstrate an improved speed-accuracy tradeoff for predicting elastic quantities of interest.

Prediction of the electron density of states for crystalline compounds with Atomistic Line Graph Neural Networks

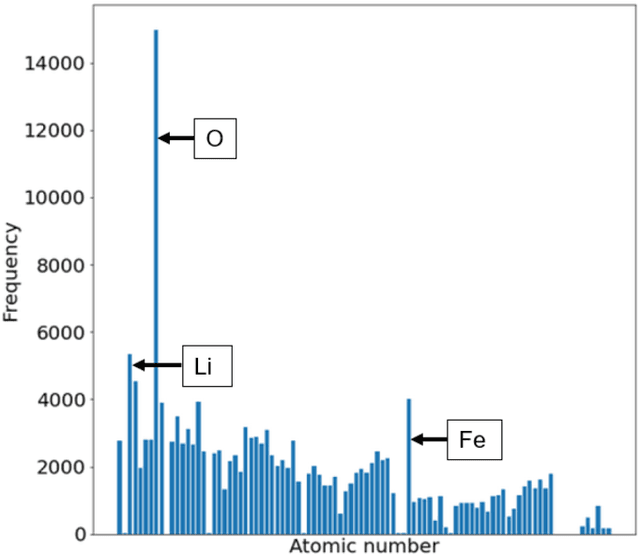
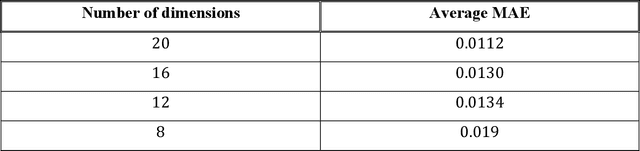
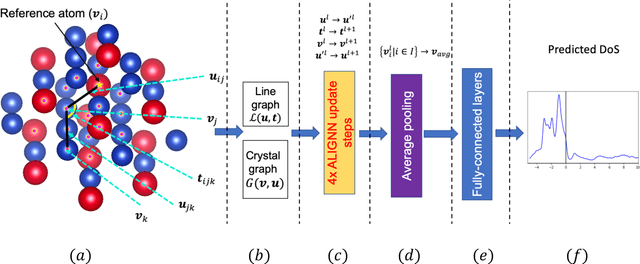
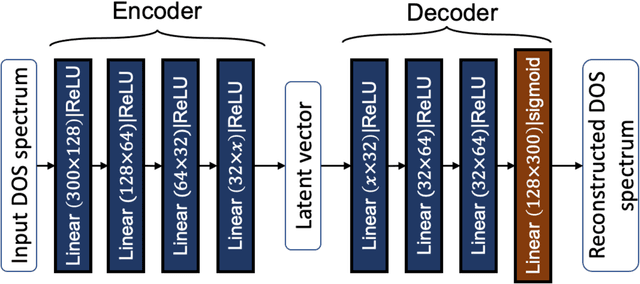
Machine learning (ML) based models have greatly enhanced the traditional materials discovery and design pipeline. Specifically, in recent years, surrogate ML models for material property prediction have demonstrated success in predicting discrete scalar-valued target properties to within reasonable accuracy of their DFT-computed values. However, accurate prediction of spectral targets such as the electron Density of States (DOS) poses a much more challenging problem due to the complexity of the target, and the limited amount of available training data. In this study, we present an extension of the recently developed Atomistic Line Graph Neural Network (ALIGNN) to accurately predict DOS of a large set of material unit cell structures, trained to the publicly available JARVIS-DFT dataset. Furthermore, we evaluate two methods of representation of the target quantity - a direct discretized spectrum, and a compressed low-dimensional representation obtained using an autoencoder. Through this work, we demonstrate the utility of graph-based featurization and modeling methods in the prediction of complex targets that depend on both chemistry and directional characteristics of material structures.

Harvesting data revolution for transmission electron microscopy (TEM) using signal processing

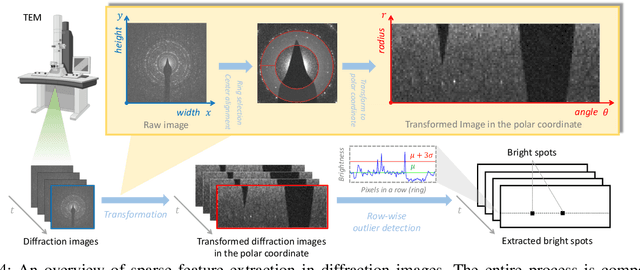
TEM (Transmission Electron Microscopy) is a powerful tool for imaging material structure and characterizing material chemistry. Recent advances in data collection technology for TEM have enabled high-volume and high-resolution data collection at a microsecond frame rate. This challenge requires the development of new data processing tools, including image analysis, feature extraction, and streaming data processing techniques. In this paper, we highlight a few areas that have benefited from combining signal processing and statistical analysis with data collection capabilities in TEM and present a future outlook in opportunities of integrating signal processing with automated TEM data analysis.

Recurrent Localization Networks applied to the Lippmann-Schwinger Equation

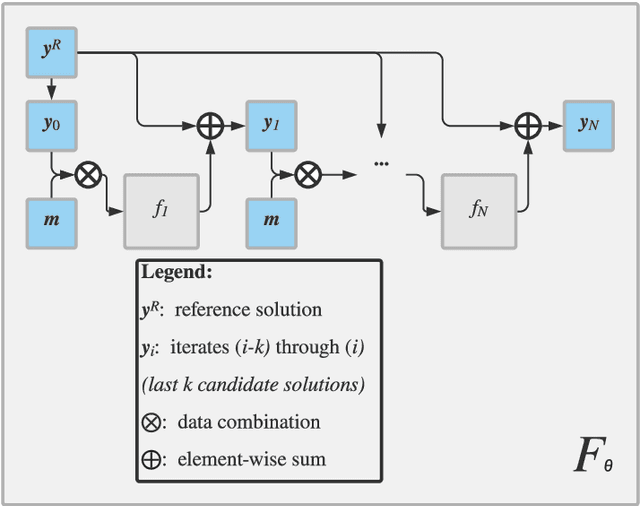
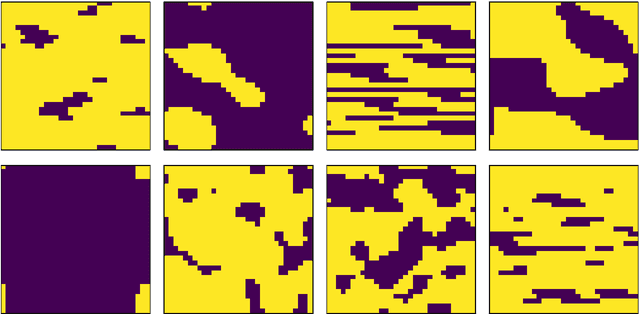
The bulk of computational approaches for modeling physical systems in materials science derive from either analytical (i.e. physics based) or data-driven (i.e. machine-learning based) origins. In order to combine the strengths of these two approaches, we advance a novel machine learning approach for solving equations of the generalized Lippmann-Schwinger (L-S) type. In this paradigm, a given problem is converted into an equivalent L-S equation and solved as an optimization problem, where the optimization procedure is calibrated to the problem at hand. As part of a learning-based loop unrolling, we use a recurrent convolutional neural network to iteratively solve the governing equations for a field of interest. This architecture leverages the generalizability and computational efficiency of machine learning approaches, but also permits a physics-based interpretation. We demonstrate our learning approach on the two-phase elastic localization problem, where it achieves excellent accuracy on the predictions of the local (i.e., voxel-level) elastic strains. Since numerous governing equations can be converted into an equivalent L-S form, the proposed architecture has potential applications across a range of multiscale materials phenomena.