Equilibrium Conserving Neural Operators for Super-Resolution Learning

Neural surrogate solvers can estimate solutions to partial differential equations in physical problems more efficiently than standard numerical methods, but require extensive high-resolution training data. In this paper, we break this limitation; we introduce a framework for super-resolution learning in solid mechanics problems. Our approach allows one to train a high-resolution neural network using only low-resolution data. Our Equilibrium Conserving Operator (ECO) architecture embeds known physics directly into the network to make up for missing high-resolution information during training. We evaluate this ECO-based super-resolution framework that strongly enforces conservation-laws in the predicted solutions on two working examples: embedded pores in a homogenized matrix and randomly textured polycrystalline materials. ECO eliminates the reliance on high-fidelity data and reduces the upfront cost of data collection by two orders of magnitude, offering a robust pathway for resource-efficient surrogate modeling in materials modeling. ECO is readily generalizable to other physics-based problems.

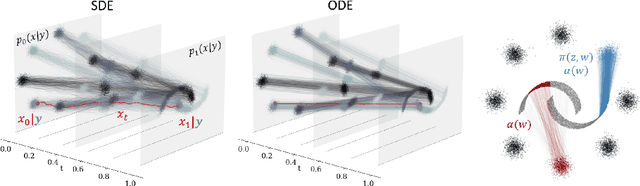
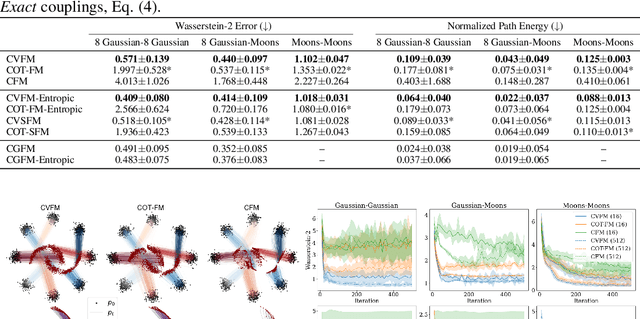
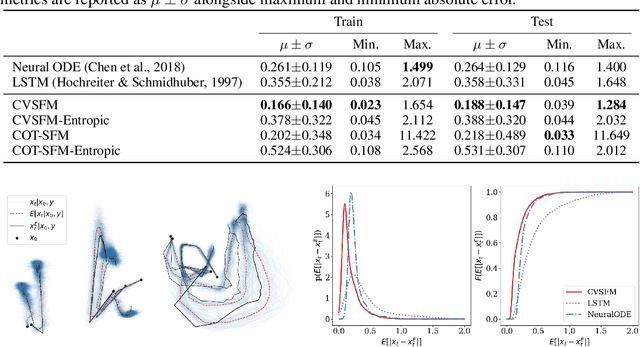
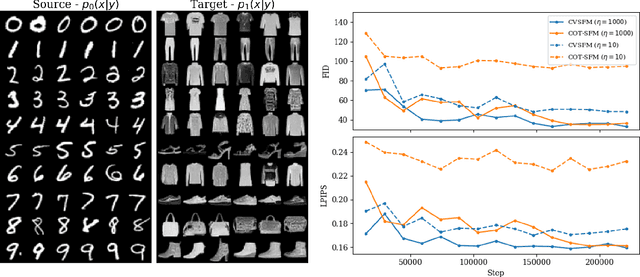
Conditional Variable Flow Matching: Transforming Conditional Densities with Amortized Conditional Optimal Transport

Forecasting stochastic nonlinear dynamical systems under the influence of conditioning variables is a fundamental challenge repeatedly encountered across the biological and physical sciences. While flow-based models can impressively predict the temporal evolution of probability distributions representing possible outcomes of a specific process, existing frameworks cannot satisfactorily account for the impact of conditioning variables on these dynamics. Amongst several limitations, existing methods require training data with paired conditions and are developed for discrete conditioning variables. We propose Conditional Variable Flow Matching (CVFM), a framework for learning flows transforming conditional distributions with amortization across continuous conditioning variables - permitting predictions across the conditional density manifold. This is accomplished through several novel advances, in particular, simultaneous sample conditioned flows over the main and conditioning variables, alongside a conditional Wasserstein distance and kernel facilitating conditional optimal transport. Collectively, these advances allow for learning system dynamics provided measurement data whose states and conditioning variables are not in correspondence. We demonstrate CVFM on a suite of increasingly challenging problems, including discrete and continuous conditional mapping benchmarks, image-to-image domain transfer, and modeling the temporal evolution of materials internal structure during manufacturing processes. We observe that CVFM results in improved performance and convergence characteristics over alternative conditional variants.