Recurrent Localization Networks applied to the Lippmann-Schwinger Equation
Paper and Code
Jan 29, 2021
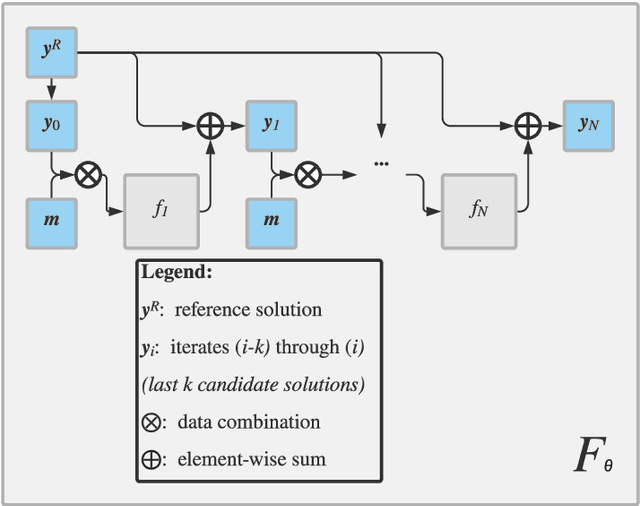

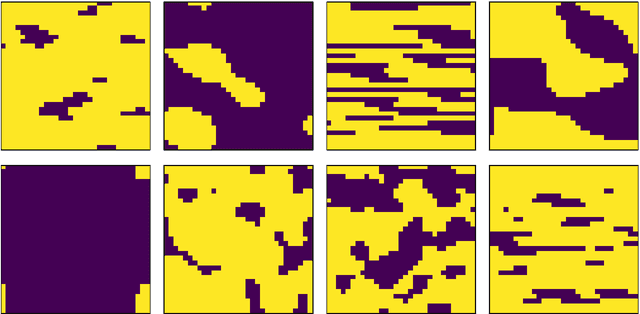
The bulk of computational approaches for modeling physical systems in materials science derive from either analytical (i.e. physics based) or data-driven (i.e. machine-learning based) origins. In order to combine the strengths of these two approaches, we advance a novel machine learning approach for solving equations of the generalized Lippmann-Schwinger (L-S) type. In this paradigm, a given problem is converted into an equivalent L-S equation and solved as an optimization problem, where the optimization procedure is calibrated to the problem at hand. As part of a learning-based loop unrolling, we use a recurrent convolutional neural network to iteratively solve the governing equations for a field of interest. This architecture leverages the generalizability and computational efficiency of machine learning approaches, but also permits a physics-based interpretation. We demonstrate our learning approach on the two-phase elastic localization problem, where it achieves excellent accuracy on the predictions of the local (i.e., voxel-level) elastic strains. Since numerous governing equations can be converted into an equivalent L-S form, the proposed architecture has potential applications across a range of multiscale materials phenomena.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge