Thermodynamically-Informed Iterative Neural Operators for Heterogeneous Elastic Localization

Engineering problems frequently require solution of governing equations with spatially-varying discontinuous coefficients. Even for linear elliptic problems, mapping large ensembles of coefficient fields to solutions can become a major computational bottleneck using traditional numerical solvers. Furthermore, machine learning methods such as neural operators struggle to fit these maps due to sharp transitions and high contrast in the coefficient fields and a scarcity of informative training data. In this work, we focus on a canonical problem in computational mechanics: prediction of local elastic deformation fields over heterogeneous material structures subjected to periodic boundary conditions. We construct a hybrid approximation for the coefficient-to-solution map using a Thermodynamically-informed Iterative Neural Operator (TherINO). Rather than using coefficient fields as direct inputs and iterating over a learned latent space, we employ thermodynamic encodings -- drawn from the constitutive equations -- and iterate over the solution space itself. Through an extensive series of case studies, we elucidate the advantages of these design choices in terms of efficiency, accuracy, and flexibility. We also analyze the model's stability and extrapolation properties on out-of-distribution coefficient fields and demonstrate an improved speed-accuracy tradeoff for predicting elastic quantities of interest.

Recurrent Localization Networks applied to the Lippmann-Schwinger Equation

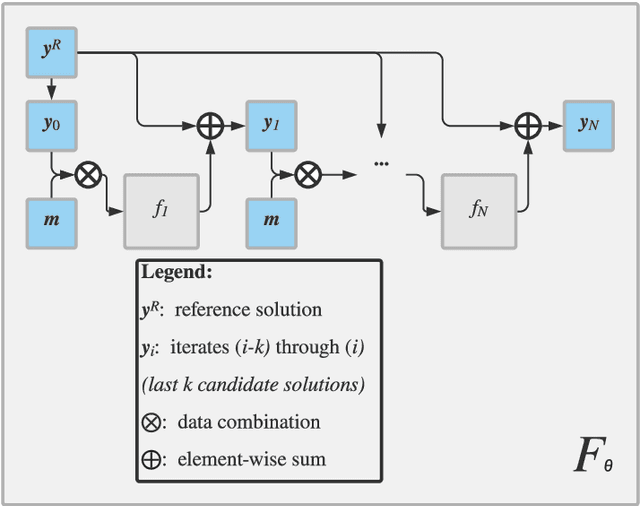
The bulk of computational approaches for modeling physical systems in materials science derive from either analytical (i.e. physics based) or data-driven (i.e. machine-learning based) origins. In order to combine the strengths of these two approaches, we advance a novel machine learning approach for solving equations of the generalized Lippmann-Schwinger (L-S) type. In this paradigm, a given problem is converted into an equivalent L-S equation and solved as an optimization problem, where the optimization procedure is calibrated to the problem at hand. As part of a learning-based loop unrolling, we use a recurrent convolutional neural network to iteratively solve the governing equations for a field of interest. This architecture leverages the generalizability and computational efficiency of machine learning approaches, but also permits a physics-based interpretation. We demonstrate our learning approach on the two-phase elastic localization problem, where it achieves excellent accuracy on the predictions of the local (i.e., voxel-level) elastic strains. Since numerous governing equations can be converted into an equivalent L-S form, the proposed architecture has potential applications across a range of multiscale materials phenomena.