Concept Drift Monitoring and Diagnostics of Supervised Learning Models via Score Vectors
Paper and Code
Dec 12, 2020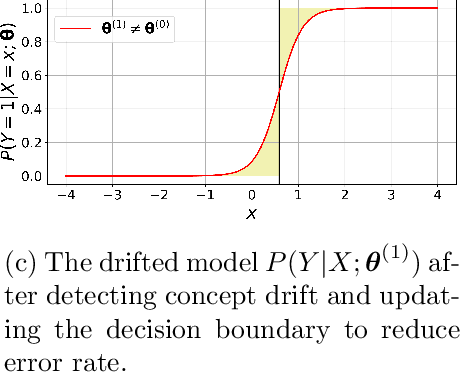
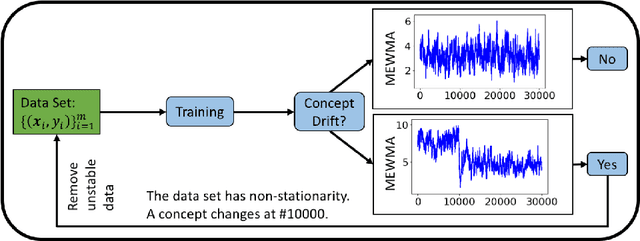
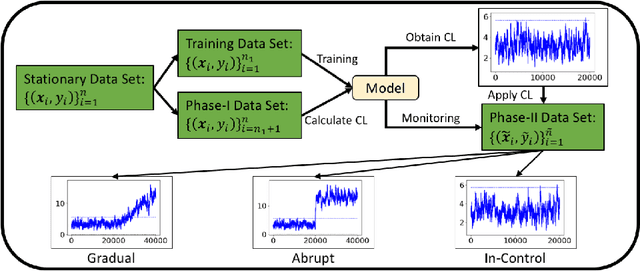
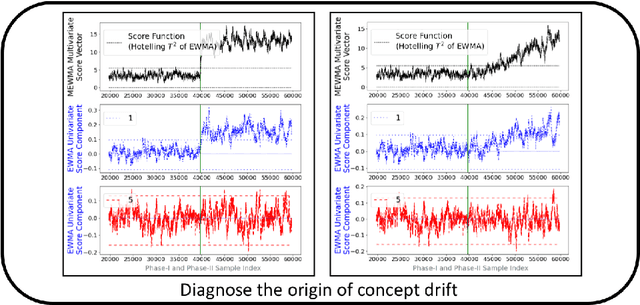
Supervised learning models are one of the most fundamental classes of models. Viewing supervised learning from a probabilistic perspective, the set of training data to which the model is fitted is usually assumed to follow a stationary distribution. However, this stationarity assumption is often violated in a phenomenon called concept drift, which refers to changes over time in the predictive relationship between covariates $\mathbf{X}$ and a response variable $Y$ and can render trained models suboptimal or obsolete. We develop a comprehensive and computationally efficient framework for detecting, monitoring, and diagnosing concept drift. Specifically, we monitor the Fisher score vector, defined as the gradient of the log-likelihood for the fitted model, using a form of multivariate exponentially weighted moving average, which monitors for general changes in the mean of a random vector. In spite of the substantial performance advantages that we demonstrate over popular error-based methods, a score-based approach has not been previously considered for concept drift monitoring. Advantages of the proposed score-based framework include applicability to any parametric model, more powerful detection of changes as shown in theory and experiments, and inherent diagnostic capabilities for helping to identify the nature of the changes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge