Bayesian Optimization for Materials Design with Mixed Quantitative and Qualitative Variables
Paper and Code
Oct 03, 2019
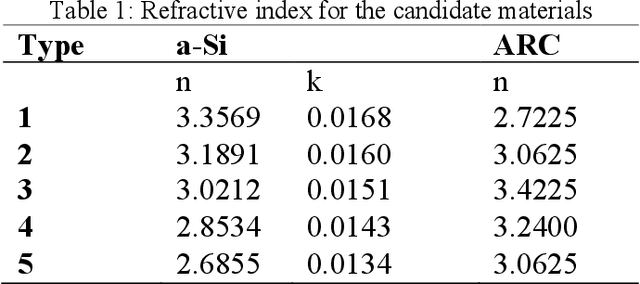
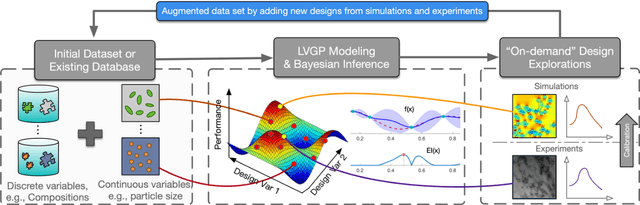

Although Bayesian Optimization (BO) has been employed for accelerating materials design in computational materials engineering, existing works are restricted to problems with quantitative variables. However, real designs of materials systems involve both qualitative and quantitative design variables representing material compositions, microstructure morphology, and processing conditions. For mixed-variable problems, existing Bayesian Optimization (BO) approaches represent qualitative factors by dummy variables first and then fit a standard Gaussian process (GP) model with numerical variables as the surrogate model. This approach is restrictive theoretically and fails to capture complex correlations between qualitative levels. We present in this paper the integration of a novel latent-variable (LV) approach for mixed-variable GP modeling with the BO framework for materials design. LVGP is a fundamentally different approach that maps qualitative design variables to underlying numerical LV in GP, which has strong physical justification. It provides flexible parameterization and representation of qualitative factors and shows superior modeling accuracy compared to the existing methods. We demonstrate our approach through testing with numerical examples and materials design examples. It is found that in all test examples the mapped LVs provide intuitive visualization and substantial insight into the nature and effects of the qualitative factors. Though materials designs are used as examples, the method presented is generic and can be utilized for other mixed variable design optimization problems that involve expensive physics-based simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge