Evaluation metrics for temporal preservation in synthetic longitudinal patient data

This study introduces a set of metrics for evaluating temporal preservation in synthetic longitudinal patient data, defined as artificially generated data that mimic real patients' repeated measurements over time. The proposed metrics assess how synthetic data reproduces key temporal characteristics, categorized into marginal, covariance, individual-level and measurement structures. We show that strong marginal-level resemblance may conceal distortions in covariance and disruptions in individual-level trajectories. Temporal preservation is influenced by factors such as original data quality, measurement frequency, and preprocessing strategies, including binning, variable encoding and precision. Variables with sparse or highly irregular measurement times provide limited information for learning temporal dependencies, resulting in reduced resemblance between the synthetic and original data. No single metric adequately captures temporal preservation; instead, a multidimensional evaluation across all characteristics provides a more comprehensive assessment of synthetic data quality. Overall, the proposed metrics clarify how and why temporal structures are preserved or degraded, enabling more reliable evaluation and improvement of generative models and supporting the creation of temporally realistic synthetic longitudinal patient data.

Methods for generating and evaluating synthetic longitudinal patient data: a systematic review

The proliferation of data in recent years has led to the advancement and utilization of various statistical and deep learning techniques, thus expediting research and development activities. However, not all industries have benefited equally from the surge in data availability, partly due to legal restrictions on data usage and privacy regulations, such as in medicine. To address this issue, various statistical disclosure and privacy-preserving methods have been proposed, including the use of synthetic data generation. Synthetic data are generated based on some existing data, with the aim of replicating them as closely as possible and acting as a proxy for real sensitive data. This paper presents a systematic review of methods for generating and evaluating synthetic longitudinal patient data, a prevalent data type in medicine. The review adheres to the PRISMA guidelines and covers literature from five databases until the end of 2022. The paper describes 17 methods, ranging from traditional simulation techniques to modern deep learning methods. The collected information includes, but is not limited to, method type, source code availability, and approaches used to assess resemblance, utility, and privacy. Furthermore, the paper discusses practical guidelines and key considerations for developing synthetic longitudinal data generation methods.

Large-Sample Properties of Non-Stationary Source Separation for Gaussian Signals

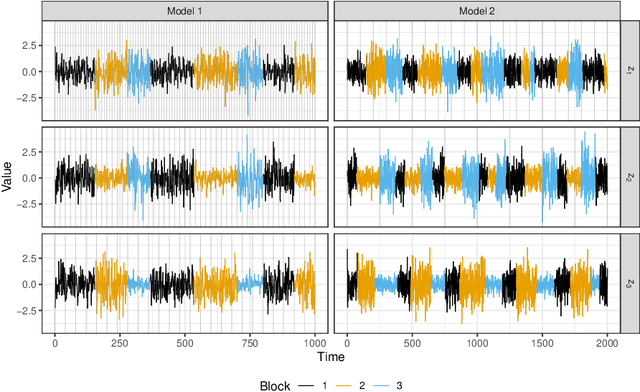
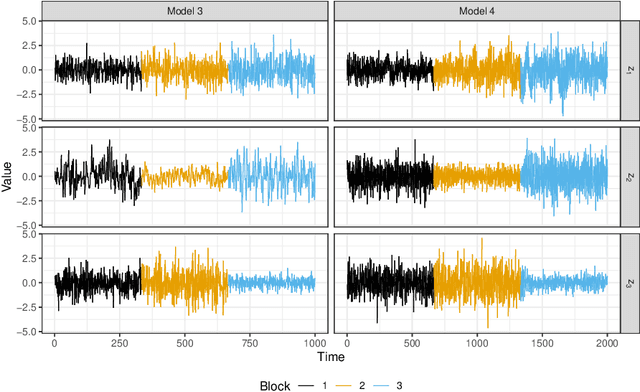
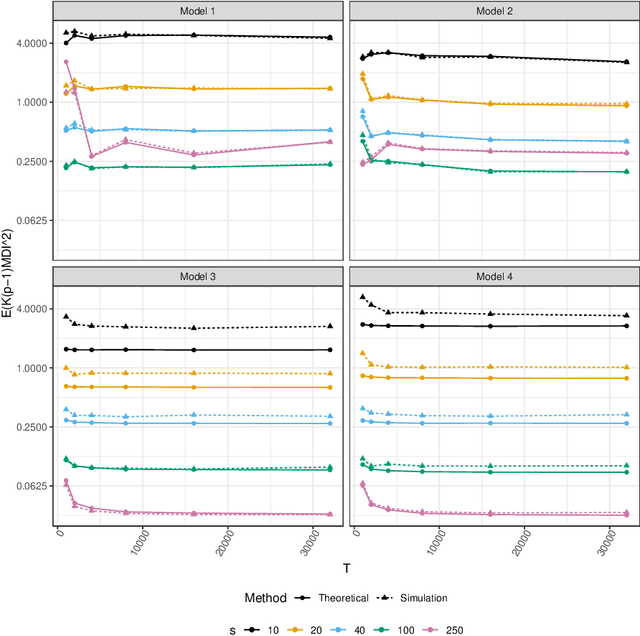
Non-stationary source separation is a well-established branch of blind source separation with many different methods. However, for none of these methods large-sample results are available. To bridge this gap, we develop large-sample theory for NSS-JD, a popular method of non-stationary source separation based on the joint diagonalization of block-wise covariance matrices. We work under an instantaneous linear mixing model for independent Gaussian non-stationary source signals together with a very general set of assumptions: besides boundedness conditions, the only assumptions we make are that the sources exhibit finite dependency and that their variance functions differ sufficiently to be asymptotically separable. The consistency of the unmixing estimator and its convergence to a limiting Gaussian distribution at the standard square root rate are shown to hold under the previous conditions. Simulation experiments are used to verify the theoretical results and to study the impact of block length on the separation.