Time-aware UNet and super-resolution deep residual networks for spatial downscaling

Satellite data of atmospheric pollutants are often available only at coarse spatial resolution, limiting their applicability in local-scale environmental analysis and decision-making. Spatial downscaling methods aim to transform the coarse satellite data into high-resolution fields. In this work, two widely used deep learning architectures, the super-resolution deep residual network (SRDRN) and the encoder-decoder-based UNet, are considered for spatial downscaling of tropospheric ozone. Both methods are extended with a lightweight temporal module, which encodes observation time using either sinusoidal or radial basis function (RBF) encoding, and fuses the temporal features with the spatial representations in the networks. The proposed time-aware extensions are evaluated against their baseline counterparts in a case study on ozone downscaling over Italy. The results suggest that, while only slightly increasing computational complexity, the temporal modules significantly improve downscaling performance and convergence speed.

Large-Sample Properties of Non-Stationary Source Separation for Gaussian Signals

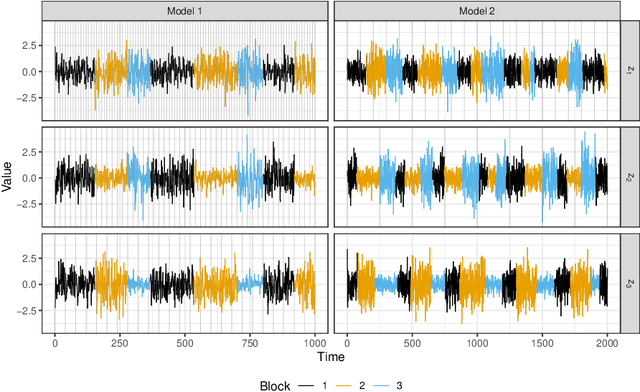
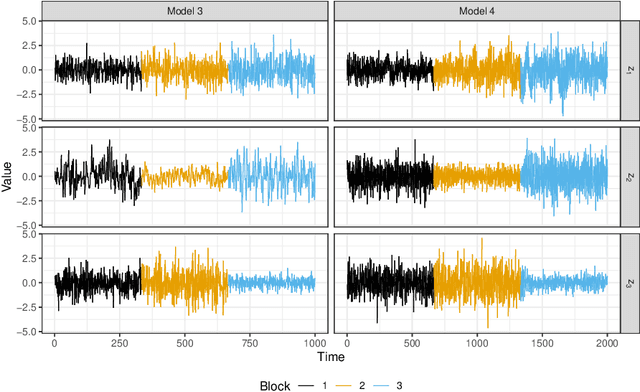
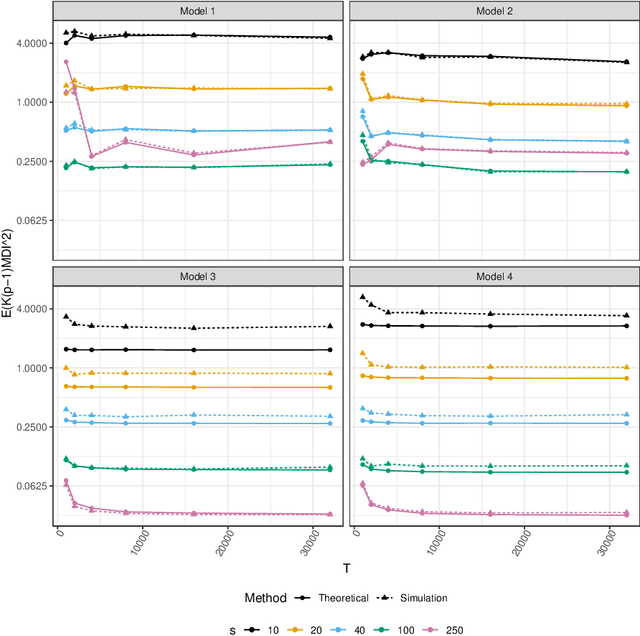
Non-stationary source separation is a well-established branch of blind source separation with many different methods. However, for none of these methods large-sample results are available. To bridge this gap, we develop large-sample theory for NSS-JD, a popular method of non-stationary source separation based on the joint diagonalization of block-wise covariance matrices. We work under an instantaneous linear mixing model for independent Gaussian non-stationary source signals together with a very general set of assumptions: besides boundedness conditions, the only assumptions we make are that the sources exhibit finite dependency and that their variance functions differ sufficiently to be asymptotically separable. The consistency of the unmixing estimator and its convergence to a limiting Gaussian distribution at the standard square root rate are shown to hold under the previous conditions. Simulation experiments are used to verify the theoretical results and to study the impact of block length on the separation.

On Cokriging, Neural Networks, and Spatial Blind Source Separation for Multivariate Spatial Prediction

Multivariate measurements taken at irregularly sampled locations are a common form of data, for example in geochemical analysis of soil. In practical considerations predictions of these measurements at unobserved locations are of great interest. For standard multivariate spatial prediction methods it is mandatory to not only model spatial dependencies but also cross-dependencies which makes it a demanding task. Recently, a blind source separation approach for spatial data was suggested. When using this spatial blind source separation method prior the actual spatial prediction, modelling of spatial cross-dependencies is avoided, which in turn simplifies the spatial prediction task significantly. In this paper we investigate the use of spatial blind source separation as a pre-processing tool for spatial prediction and compare it with predictions from Cokriging and neural networks in an extensive simulation study as well as a geochemical dataset.