Breakdown properties of optimal transport maps: general transportation costs

Two recent works, Avella-Medina and González-Sanz (2026) and Passeggeri and Paindaveine (2026), studied the robustness of the optimal transport map through its breakdown point, i.e., the smallest fraction of contamination that can make the map take arbitrarily aberrant values. Their main finding is the following: let $P$ and $Q$ denote the target and reference measures, respectively, and let $T$ be the optimal transport map for the squared Euclidean cost. Then, the breakdown point of $T(u)$, when $P$ is perturbed and $Q$ is fixed, coincides with the Tukey depth of $u$ relative to $Q$. In this note, we extend this result to general convex cost functions, demonstrating that the cost function does not have any impact on the breakdown point of the optimal transport map. Our contribution provides a definitive characterization of the breakdown point of the optimal transport map. In particular, it shows that for a broad class of regular cost functions, all transport-based quantiles enjoy the same high breakdown point properties.

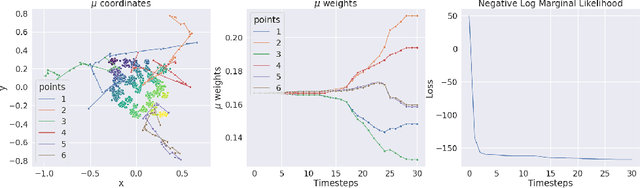
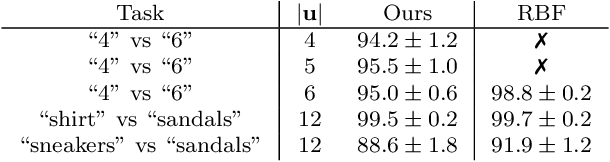
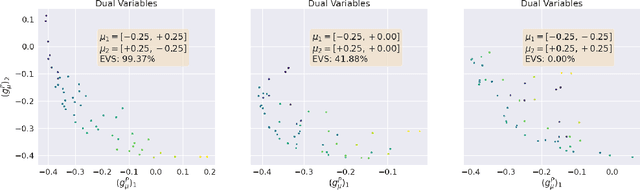
Gaussian Processes on Distributions based on Regularized Optimal Transport

We present a novel kernel over the space of probability measures based on the dual formulation of optimal regularized transport. We propose an Hilbertian embedding of the space of probabilities using their Sinkhorn potentials, which are solutions of the dual entropic relaxed optimal transport between the probabilities and a reference measure $\mathcal{U}$. We prove that this construction enables to obtain a valid kernel, by using the Hilbert norms. We prove that the kernel enjoys theoretical properties such as universality and some invariances, while still being computationally feasible. Moreover we provide theoretical guarantees on the behaviour of a Gaussian process based on this kernel. The empirical performances are compared with other traditional choices of kernels for processes indexed on distributions.

An improved central limit theorem and fast convergence rates for entropic transportation costs

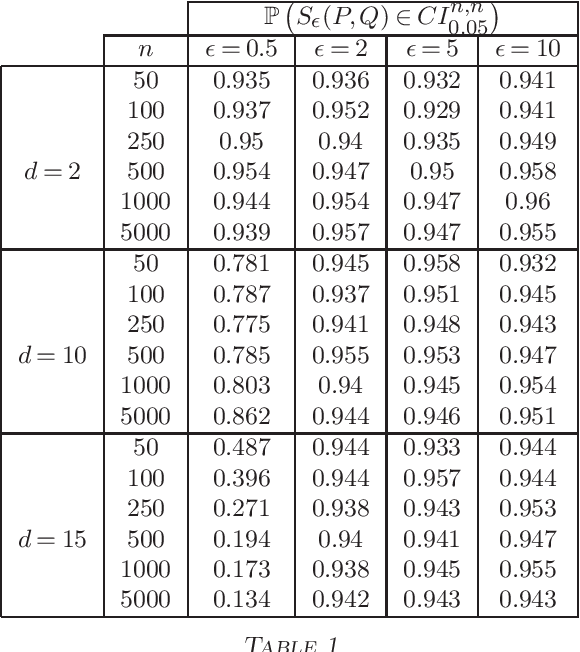
We prove a central limit theorem for the entropic transportation cost between subgaussian probability measures, centered at the population cost. This is the first result which allows for asymptotically valid inference for entropic optimal transport between measures which are not necessarily discrete. In the compactly supported case, we complement these results with new, faster, convergence rates for the expected entropic transportation cost between empirical measures. Our proof is based on strengthening convergence results for dual solutions to the entropic optimal transport problem.