An improved central limit theorem and fast convergence rates for entropic transportation costs

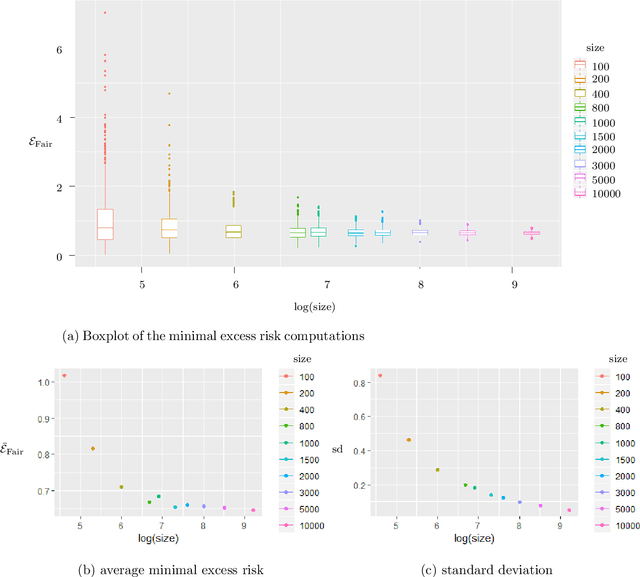
We prove a central limit theorem for the entropic transportation cost between subgaussian probability measures, centered at the population cost. This is the first result which allows for asymptotically valid inference for entropic optimal transport between measures which are not necessarily discrete. In the compactly supported case, we complement these results with new, faster, convergence rates for the expected entropic transportation cost between empirical measures. Our proof is based on strengthening convergence results for dual solutions to the entropic optimal transport problem.

The statistical effect of entropic regularization in optimal transportation

We propose to tackle the problem of understanding the effect of regularization in Sinkhorn algotihms. In the case of Gaussian distributions we provide a closed form for the regularized optimal transport which enables to provide a better understanding of the effect of the regularization from a statistical framework.

Achieving robustness in classification using optimal transport with hinge regularization

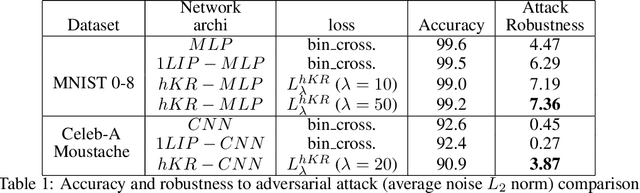
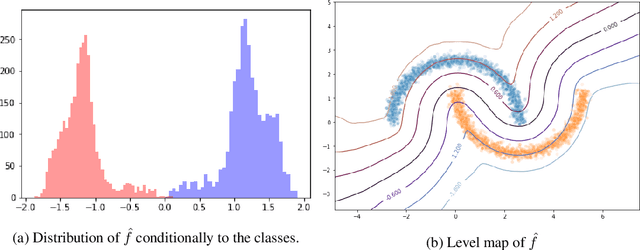
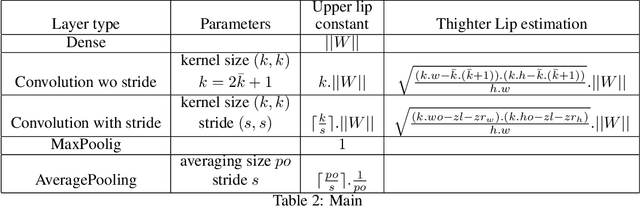
We propose a new framework for robust binary classification, with Deep Neural Networks, based on a hinge regularization of the Kantorovich-Rubinstein dual formulation for the estimation of the Wasserstein distance. The robustness of the approach is guaranteed by the strict Lipschitz constraint on functions required by the optimization problem and direct interpretation of the loss in terms of adversarial robustness. We prove that this classification formulation has a solution, and is still the dual formulation of an optimal transportation problem. We also establish the geometrical properties of this optimal solution. We summarize state-of-the-art methods to enforce Lipschitz constraints on neural networks and we propose new ones for convolutional networks (associated with an open source library for this purpose). The experiments show that the approach provides the expected guarantees in terms of robustness without any significant accuracy drop. The results also suggest that adversarial attacks on the proposed models visibly and meaningfully change the input, and can thus serve as an explanation for the classification.

Review of Mathematical frameworks for Fairness in Machine Learning

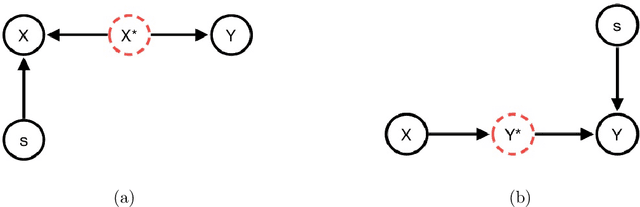
A review of the main fairness definitions and fair learning methodologies proposed in the literature over the last years is presented from a mathematical point of view. Following our independence-based approach, we consider how to build fair algorithms and the consequences on the degradation of their performance compared to the possibly unfair case. This corresponds to the price for fairness given by the criteria $\textit{statistical parity}$ or $\textit{equality of odds}$. Novel results giving the expressions of the optimal fair classifier and the optimal fair predictor (under a linear regression gaussian model) in the sense of $\textit{equality of odds}$ are presented.

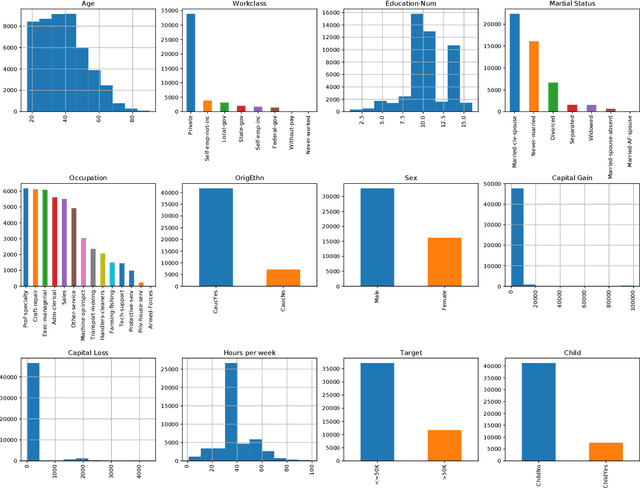
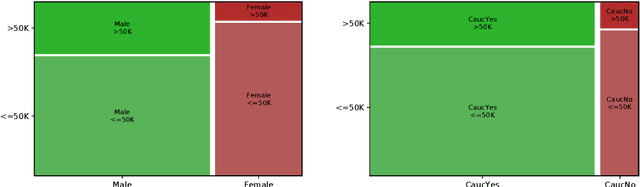
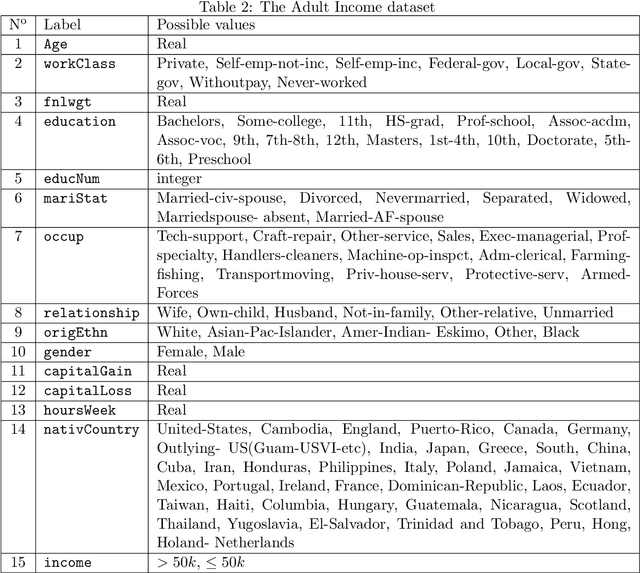
A survey of bias in Machine Learning through the prism of Statistical Parity for the Adult Data Set

Applications based on Machine Learning models have now become an indispensable part of the everyday life and the professional world. A critical question then recently arised among the population: Do algorithmic decisions convey any type of discrimination against specific groups of population or minorities? In this paper, we show the importance of understanding how a bias can be introduced into automatic decisions. We first present a mathematical framework for the fair learning problem, specifically in the binary classification setting. We then propose to quantify the presence of bias by using the standard Disparate Impact index on the real and well-known Adult income data set. Finally, we check the performance of different approaches aiming to reduce the bias in binary classification outcomes. Importantly, we show that some intuitive methods are ineffective. This sheds light on the fact trying to make fair machine learning models may be a particularly challenging task, in particular when the training observations contain a bias.

optimalFlow: Optimal-transport approach to flow cytometry gating and population matching

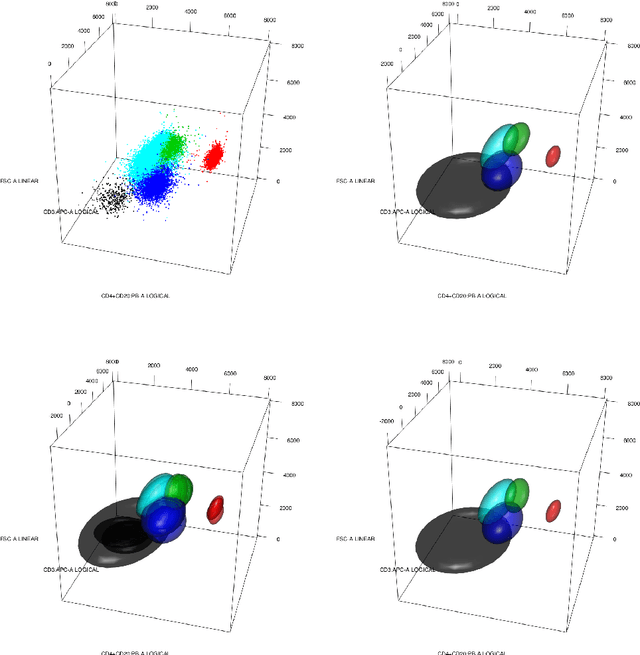
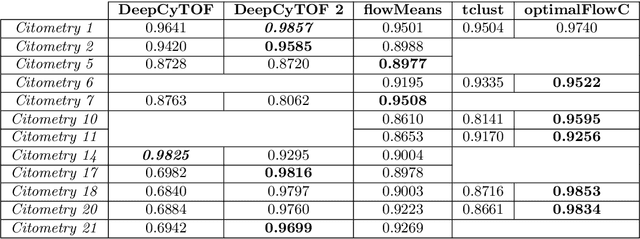
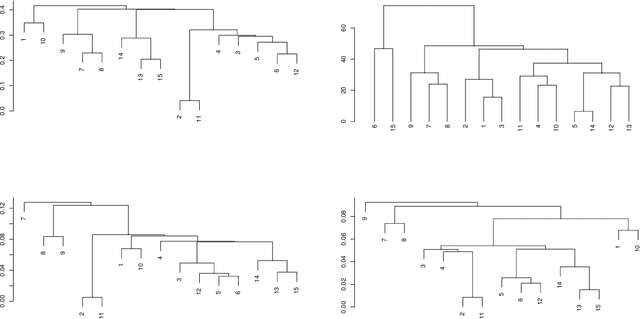
Data used in Flow Cytometry present pronounced variability due to biological and technical reasons. Biological variability is a well known phenomenon produced by measurements on different individuals, with different characteristics such as age, sex, etc... The use of different settings for measurement, the variation of the conditions during experiments or the different types of flow cytometers are some of the technical sources of variability. This high variability makes difficult the use of supervised machine learning for identification of cell populations. We propose optimalFlowTemplates, based on a similarity distance and Wasserstein barycenters, which clusterizes cytometries and produces prototype cytometries for the different groups. We show that supervised learning restricted to the new groups performs better than the same techniques applied to the whole collection. We also present optimalFlowClassification, which uses a database of gated cytometries and optimalFlowTemplates to assign cell types to a new cytometry. We show that this procedure can outperform state of the art techniques in the proposed datasets. Our code and data are freely available as R packages at https://github.com/HristoInouzhe/optimalFlow and https://github.com/HristoInouzhe/optimalFlowData.

Attraction-Repulsion clustering with applications to fairness

In the framework of fair learning, we consider clustering methods that avoid or limit the influence of a set of protected attributes, $S$, (race, sex, etc) over the resulting clusters, with the goal of producing a fair clustering. For this, we introduce perturbations to the Euclidean distance that take into account $S$ in a way that resembles attraction-repulsion in charged particles in Physics and results in dissimilarities with an easy interpretation. Cluster analysis based on these dissimilarities penalizes homogeneity of the clusters in the attributes $S$, and leads to an improvement in fairness. We illustrate the use of our procedures with both synthetic and real data.

Confidence Intervals for Testing Disparate Impact in Fair Learning

We provide the asymptotic distribution of the major indexes used in the statistical literature to quantify disparate treatment in machine learning. We aim at promoting the use of confidence intervals when testing the so-called group disparate impact. We illustrate on some examples the importance of using confidence intervals and not a single value.