A Near-Optimal Algorithm for Univariate Zeroth-Order Budget Convex Optimization
Paper and Code
Aug 13, 2022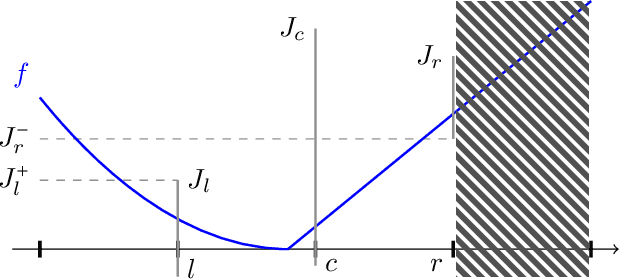
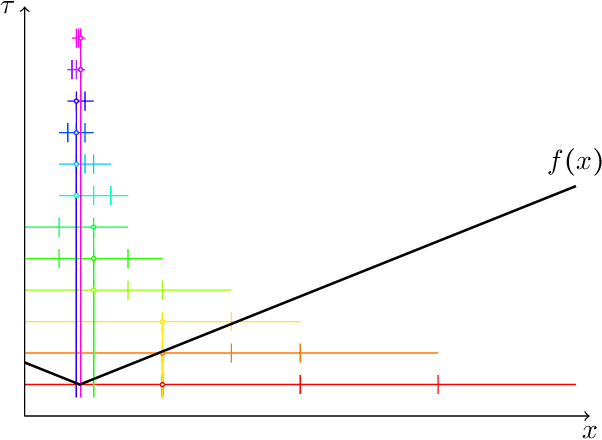
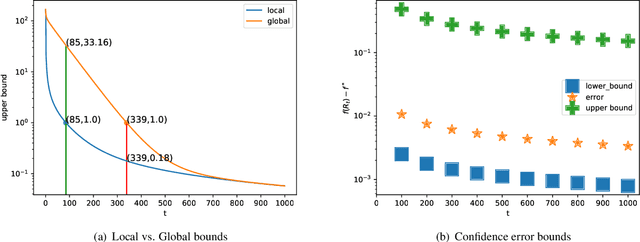
This paper studies a natural generalization of the problem of minimizing a univariate convex function $f$ by querying its values sequentially. At each time-step $t$, the optimizer can invest a budget $b_t$ in a query point $X_t$ of their choice to obtain a fuzzy evaluation of $f$ at $X_t$ whose accuracy depends on the amount of budget invested in $X_t$ across times. This setting is motivated by the minimization of objectives whose values can only be determined approximately through lengthy or expensive computations. We design an any-time parameter-free algorithm called Dyadic Search, for which we prove near-optimal optimization error guarantees. As a byproduct of our analysis, we show that the classical dependence on the global Lipschitz constant in the error bounds is an artifact of the granularity of the budget. Finally, we illustrate our theoretical findings with numerical simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge