Geometry-induced Implicit Regularization in Deep ReLU Neural Networks

It is well known that neural networks with many more parameters than training examples do not overfit. Implicit regularization phenomena, which are still not well understood, occur during optimization and 'good' networks are favored. Thus the number of parameters is not an adequate measure of complexity if we do not consider all possible networks but only the 'good' ones. To better understand which networks are favored during optimization, we study the geometry of the output set as parameters vary. When the inputs are fixed, we prove that the dimension of this set changes and that the local dimension, called batch functional dimension, is almost surely determined by the activation patterns in the hidden layers. We prove that the batch functional dimension is invariant to the symmetries of the network parameterization: neuron permutations and positive rescalings. Empirically, we establish that the batch functional dimension decreases during optimization. As a consequence, optimization leads to parameters with low batch functional dimensions. We call this phenomenon geometry-induced implicit regularization.The batch functional dimension depends on both the network parameters and inputs. To understand the impact of the inputs, we study, for fixed parameters, the largest attainable batch functional dimension when the inputs vary. We prove that this quantity, called computable full functional dimension, is also invariant to the symmetries of the network's parameterization, and is determined by the achievable activation patterns. We also provide a sampling theorem, showing a fast convergence of the estimation of the computable full functional dimension for a random input of increasing size. Empirically we find that the computable full functional dimension remains close to the number of parameters, which is related to the notion of local identifiability. This differs from the observed values for the batch functional dimension computed on training inputs and test inputs. The latter are influenced by geometry-induced implicit regularization.

Local Identifiability of Deep ReLU Neural Networks: the Theory

Is a sample rich enough to determine, at least locally, the parameters of a neural network? To answer this question, we introduce a new local parameterization of a given deep ReLU neural network by fixing the values of some of its weights. This allows us to define local lifting operators whose inverses are charts of a smooth manifold of a high dimensional space. The function implemented by the deep ReLU neural network composes the local lifting with a linear operator which depends on the sample. We derive from this convenient representation a geometrical necessary and sufficient condition of local identifiability. Looking at tangent spaces, the geometrical condition provides: 1/ a sharp and testable necessary condition of identifiability and 2/ a sharp and testable sufficient condition of local identifiability. The validity of the conditions can be tested numerically using backpropagation and matrix rank computations.

Parameter identifiability of a deep feedforward ReLU neural network

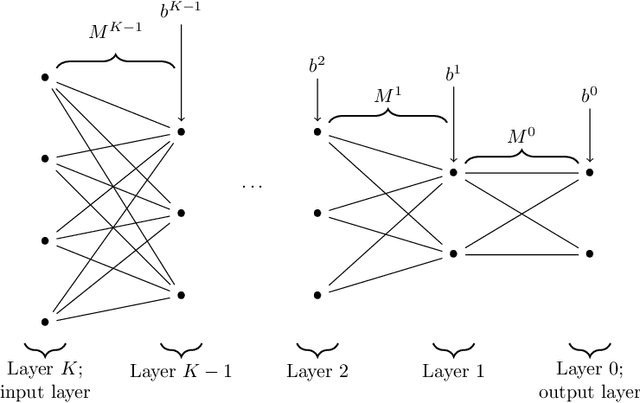
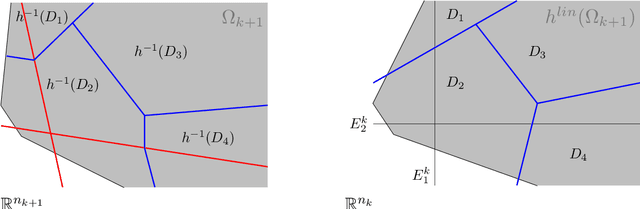
The possibility for one to recover the parameters-weights and biases-of a neural network thanks to the knowledge of its function on a subset of the input space can be, depending on the situation, a curse or a blessing. On one hand, recovering the parameters allows for better adversarial attacks and could also disclose sensitive information from the dataset used to construct the network. On the other hand, if the parameters of a network can be recovered, it guarantees the user that the features in the latent spaces can be interpreted. It also provides foundations to obtain formal guarantees on the performances of the network. It is therefore important to characterize the networks whose parameters can be identified and those whose parameters cannot. In this article, we provide a set of conditions on a deep fully-connected feedforward ReLU neural network under which the parameters of the network are uniquely identified-modulo permutation and positive rescaling-from the function it implements on a subset of the input space.