Zebra: In-Context and Generative Pretraining for Solving Parametric PDEs
Paper and Code
Oct 04, 2024
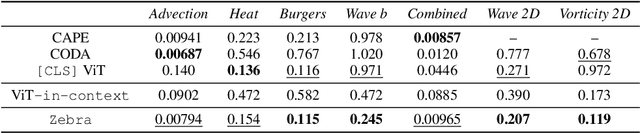
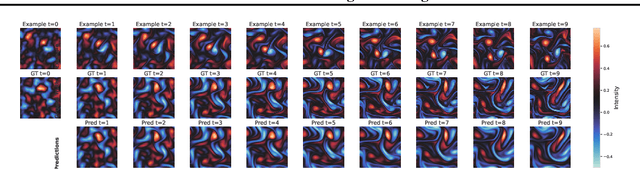
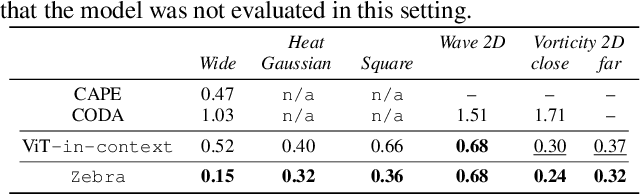
Solving time-dependent parametric partial differential equations (PDEs) is challenging, as models must adapt to variations in parameters such as coefficients, forcing terms, and boundary conditions. Data-driven neural solvers either train on data sampled from the PDE parameters distribution in the hope that the model generalizes to new instances or rely on gradient-based adaptation and meta-learning to implicitly encode the dynamics from observations. This often comes with increased inference complexity. Inspired by the in-context learning capabilities of large language models (LLMs), we introduce Zebra, a novel generative auto-regressive transformer designed to solve parametric PDEs without requiring gradient adaptation at inference. By leveraging in-context information during both pre-training and inference, Zebra dynamically adapts to new tasks by conditioning on input sequences that incorporate context trajectories or preceding states. This approach enables Zebra to flexibly handle arbitrarily sized context inputs and supports uncertainty quantification through the sampling of multiple solution trajectories. We evaluate Zebra across a variety of challenging PDE scenarios, demonstrating its adaptability, robustness, and superior performance compared to existing approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge