Beyond Euclid: An Illustrated Guide to Modern Machine Learning with Geometric, Topological, and Algebraic Structures

The enduring legacy of Euclidean geometry underpins classical machine learning, which, for decades, has been primarily developed for data lying in Euclidean space. Yet, modern machine learning increasingly encounters richly structured data that is inherently nonEuclidean. This data can exhibit intricate geometric, topological and algebraic structure: from the geometry of the curvature of space-time, to topologically complex interactions between neurons in the brain, to the algebraic transformations describing symmetries of physical systems. Extracting knowledge from such non-Euclidean data necessitates a broader mathematical perspective. Echoing the 19th-century revolutions that gave rise to non-Euclidean geometry, an emerging line of research is redefining modern machine learning with non-Euclidean structures. Its goal: generalizing classical methods to unconventional data types with geometry, topology, and algebra. In this review, we provide an accessible gateway to this fast-growing field and propose a graphical taxonomy that integrates recent advances into an intuitive unified framework. We subsequently extract insights into current challenges and highlight exciting opportunities for future development in this field.

Bispectral Neural Networks

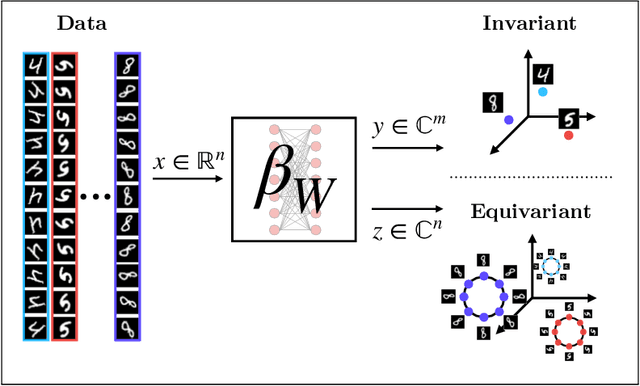
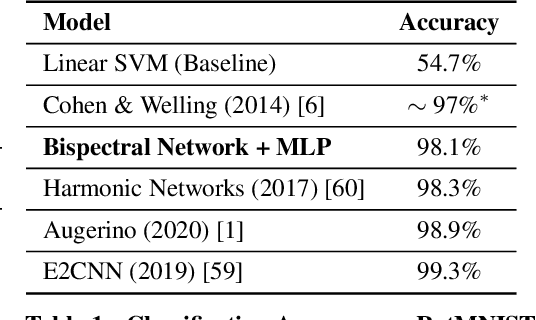
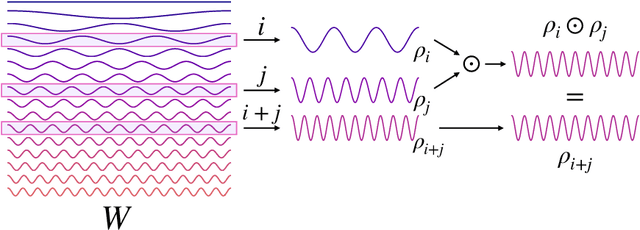
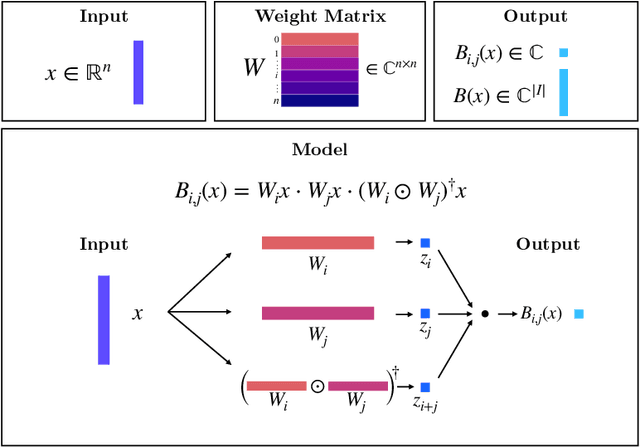
We present a novel machine learning architecture, Bispectral Neural Networks (BNNs), for learning representations of data that are invariant to the actions of groups on the space over which a signal is defined. The model incorporates the ansatz of the bispectrum, an analytically defined group invariant that is complete--that is, it preserves all signal structure while removing only the variation due to group actions. Here, we demonstrate that BNNs are able to discover arbitrary commutative group structure in data, with the trained models learning the irreducible representations of the groups, which allows for the recovery of the group Cayley tables. Remarkably, trained networks learn to approximate bispectra on these groups, and thus possess the robustness, completeness, and generality of the analytical object.

Geomstats: A Python Package for Riemannian Geometry in Machine Learning

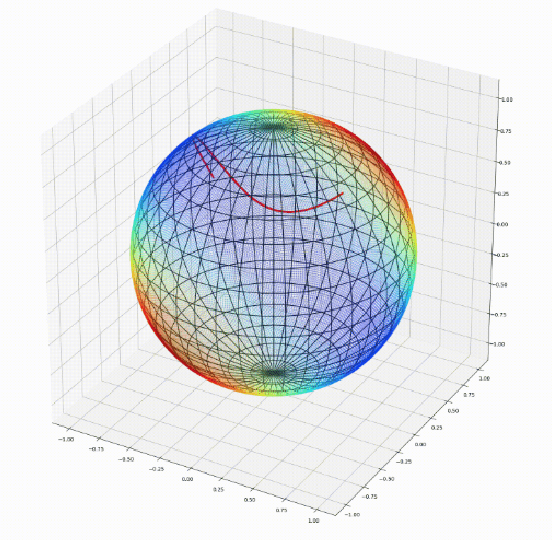
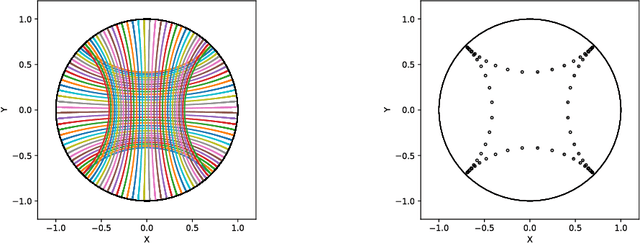
We introduce Geomstats, an open-source Python toolbox for computations and statistics on nonlinear manifolds, such as hyperbolic spaces, spaces of symmetric positive definite matrices, Lie groups of transformations, and many more. We provide object-oriented and extensively unit-tested implementations. Among others, manifolds come equipped with families of Riemannian metrics, with associated exponential and logarithmic maps, geodesics and parallel transport. Statistics and learning algorithms provide methods for estimation, clustering and dimension reduction on manifolds. All associated operations are vectorized for batch computation and provide support for different execution backends, namely NumPy, PyTorch and TensorFlow, enabling GPU acceleration. This paper presents the package, compares it with related libraries and provides relevant code examples. We show that Geomstats provides reliable building blocks to foster research in differential geometry and statistics, and to democratize the use of Riemannian geometry in machine learning applications. The source code is freely available under the MIT license at \url{geomstats.ai}.