Bispectral Neural Networks
Paper and Code
Sep 09, 2022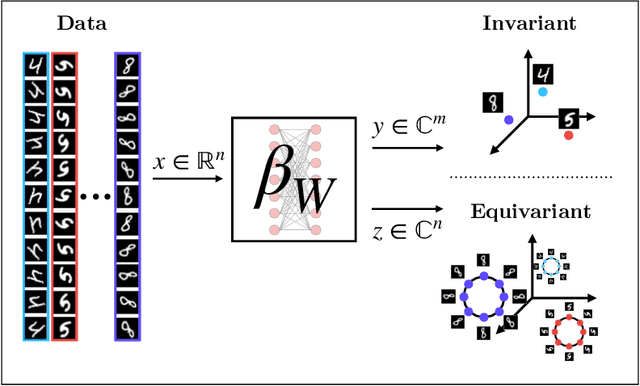
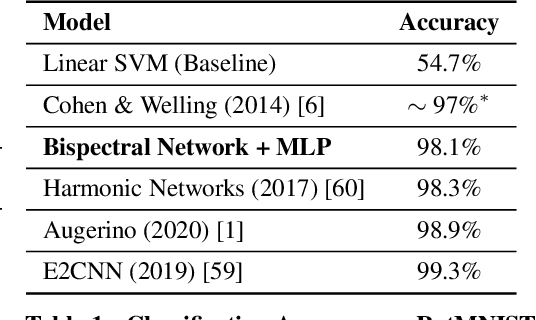
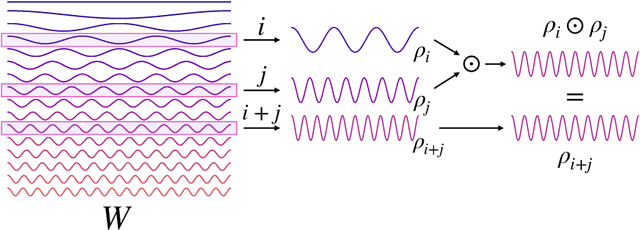
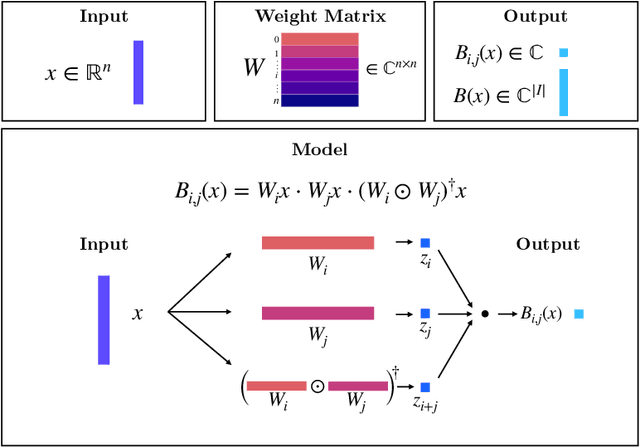
We present a novel machine learning architecture, Bispectral Neural Networks (BNNs), for learning representations of data that are invariant to the actions of groups on the space over which a signal is defined. The model incorporates the ansatz of the bispectrum, an analytically defined group invariant that is complete--that is, it preserves all signal structure while removing only the variation due to group actions. Here, we demonstrate that BNNs are able to discover arbitrary commutative group structure in data, with the trained models learning the irreducible representations of the groups, which allows for the recovery of the group Cayley tables. Remarkably, trained networks learn to approximate bispectra on these groups, and thus possess the robustness, completeness, and generality of the analytical object.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge