LOBSTUR: A Local Bootstrap Framework for Tuning Unsupervised Representations in Graph Neural Networks

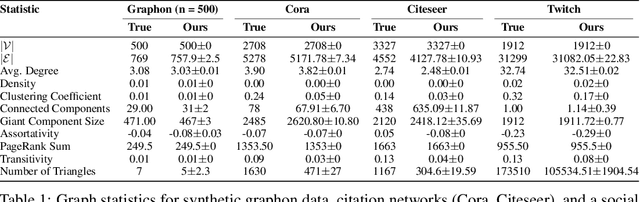
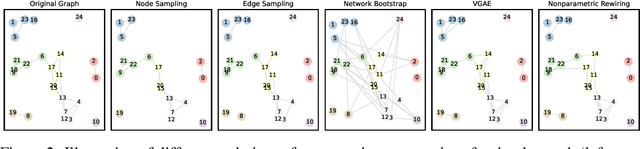
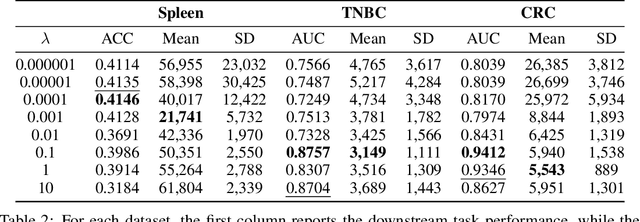
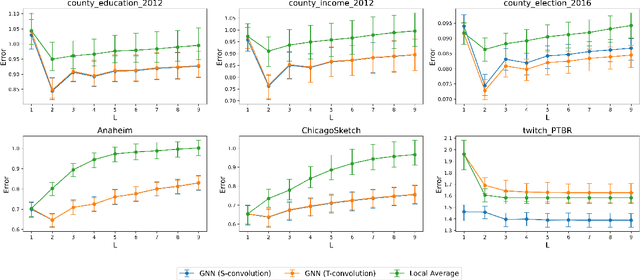
Graph Neural Networks (GNNs) are increasingly used in conjunction with unsupervised learning techniques to learn powerful node representations, but their deployment is hindered by their high sensitivity to hyperparameter tuning and the absence of established methodologies for selecting the optimal models. To address these challenges, we propose LOBSTUR-GNN ({\bf Lo}cal {\bf B}oot{\bf s}trap for {\bf T}uning {\bf U}nsupervised {\bf R}epresentations in GNNs) i), a novel framework designed to adapt bootstrapping techniques for unsupervised graph representation learning. LOBSTUR-GNN tackles two main challenges: (a) adapting the bootstrap edge and feature resampling process to account for local graph dependencies in creating alternative versions of the same graph, and (b) establishing robust metrics for evaluating learned representations without ground-truth labels. Using locally bootstrapped resampling and leveraging Canonical Correlation Analysis (CCA) to assess embedding consistency, LOBSTUR provides a principled approach for hyperparameter tuning in unsupervised GNNs. We validate the effectiveness and efficiency of our proposed method through extensive experiments on established academic datasets, showing an 65.9\% improvement in the classification accuracy compared to an uninformed selection of hyperparameters. Finally, we deploy our framework on a real-world application, thereby demonstrating its validity and practical utility in various settings. \footnote{The code is available at \href{https://github.com/sowonjeong/lobstur-graph-bootstrap}{github.com/sowonjeong/lobstur-graph-bootstrap}.}

Graph-Structured Topic Modeling for Documents with Spatial or Covariate Dependencies

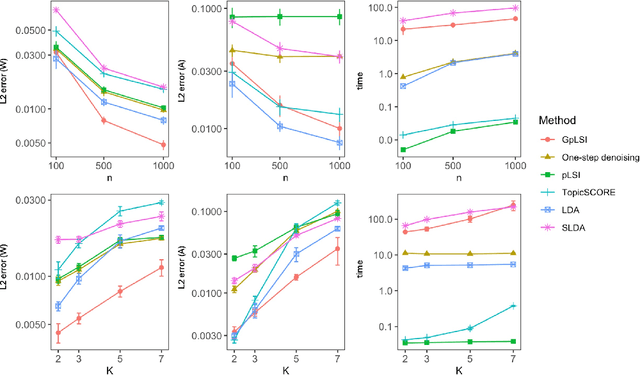
We address the challenge of incorporating document-level metadata into topic modeling to improve topic mixture estimation. To overcome the computational complexity and lack of theoretical guarantees in existing Bayesian methods, we extend probabilistic latent semantic indexing (pLSI), a frequentist framework for topic modeling, by incorporating document-level covariates or known similarities between documents through a graph formalism. Modeling documents as nodes and edges denoting similarities, we propose a new estimator based on a fast graph-regularized iterative singular value decomposition (SVD) that encourages similar documents to share similar topic mixture proportions. We characterize the estimation error of our proposed method by deriving high-probability bounds and develop a specialized cross-validation method to optimize our regularization parameters. We validate our model through comprehensive experiments on synthetic datasets and three real-world corpora, demonstrating improved performance and faster inference compared to existing Bayesian methods.

Understanding the Effect of GCN Convolutions in Regression Tasks

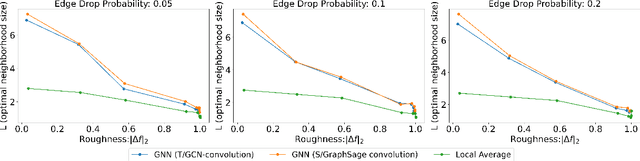
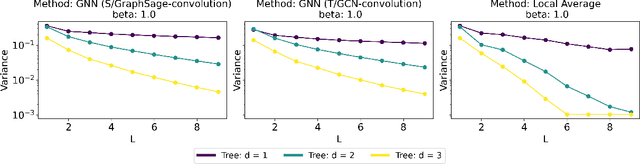
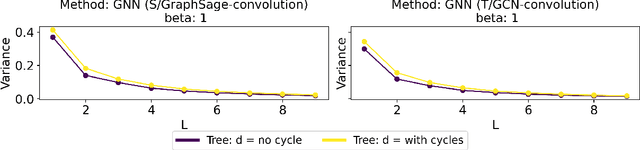
Graph Convolutional Networks (GCNs) have become a pivotal method in machine learning for modeling functions over graphs. Despite their widespread success across various applications, their statistical properties (e.g. consistency, convergence rates) remain ill-characterized. To begin addressing this knowledge gap, in this paper, we provide a formal analysis of the impact of convolution operators on regression tasks over homophilic networks. Focusing on estimators based solely on neighborhood aggregation, we examine how two common convolutions - the original GCN and GraphSage convolutions - affect the learning error as a function of the neighborhood topology and the number of convolutional layers. We explicitly characterize the bias-variance trade-off incurred by GCNs as a function of the neighborhood size and identify specific graph topologies where convolution operators are less effective. Our theoretical findings are corroborated by synthetic experiments, and provide a start to a deeper quantitative understanding of convolutional effects in GCNs for offering rigorous guidelines for practitioners.

GNUMAP: A Parameter-Free Approach to Unsupervised Dimensionality Reduction via Graph Neural Networks

With the proliferation of Graph Neural Network (GNN) methods stemming from contrastive learning, unsupervised node representation learning for graph data is rapidly gaining traction across various fields, from biology to molecular dynamics, where it is often used as a dimensionality reduction tool. However, there remains a significant gap in understanding the quality of the low-dimensional node representations these methods produce, particularly beyond well-curated academic datasets. To address this gap, we propose here the first comprehensive benchmarking of various unsupervised node embedding techniques tailored for dimensionality reduction, encompassing a range of manifold learning tasks, along with various performance metrics. We emphasize the sensitivity of current methods to hyperparameter choices -- highlighting a fundamental issue as to their applicability in real-world settings where there is no established methodology for rigorous hyperparameter selection. Addressing this issue, we introduce GNUMAP, a robust and parameter-free method for unsupervised node representation learning that merges the traditional UMAP approach with the expressivity of the GNN framework. We show that GNUMAP consistently outperforms existing state-of-the-art GNN embedding methods in a variety of contexts, including synthetic geometric datasets, citation networks, and real-world biomedical data -- making it a simple but reliable dimensionality reduction tool.

A Simplified Framework for Contrastive Learning for Node Representations

Contrastive learning has recently established itself as a powerful self-supervised learning framework for extracting rich and versatile data representations. Broadly speaking, contrastive learning relies on a data augmentation scheme to generate two versions of the input data and learns low-dimensional representations by maximizing a normalized temperature-scaled cross entropy loss (NT-Xent) to identify augmented samples corresponding to the same original entity. In this paper, we investigate the potential of deploying contrastive learning in combination with Graph Neural Networks for embedding nodes in a graph. Specifically, we show that the quality of the resulting embeddings and training time can be significantly improved by a simple column-wise postprocessing of the embedding matrix, instead of the row-wise postprocessing via multilayer perceptrons (MLPs) that is adopted by the majority of peer methods. This modification yields improvements in downstream classification tasks of up to 1.5% and even beats existing state-of-the-art approaches on 6 out of 8 different benchmarks. We justify our choices of postprocessing by revisiting the "alignment vs. uniformity paradigm", and show that column-wise post-processing improves both "alignment" and "uniformity" of the embeddings.

Tuning the Geometry of Graph Neural Networks

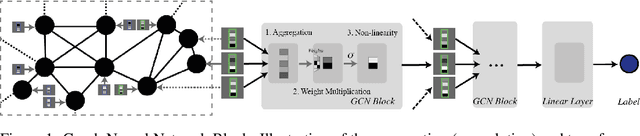
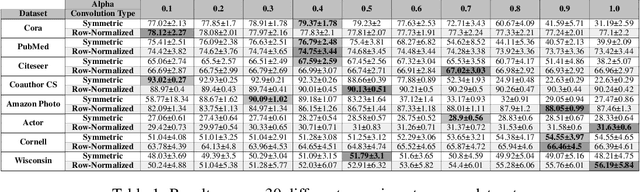
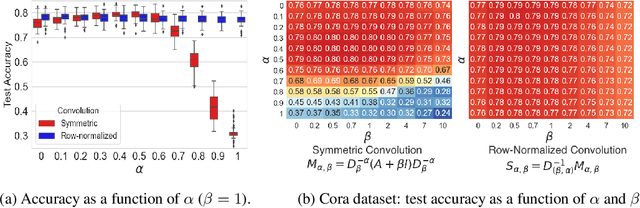
By recursively summing node features over entire neighborhoods, spatial graph convolution operators have been heralded as key to the success of Graph Neural Networks (GNNs). Yet, despite the multiplication of GNN methods across tasks and applications, the impact of this aggregation operation on their performance still has yet to be extensively analysed. In fact, while efforts have mostly focused on optimizing the architecture of the neural network, fewer works have attempted to characterize (a) the different classes of spatial convolution operators, (b) how the choice of a particular class relates to properties of the data , and (c) its impact on the geometry of the embedding space. In this paper, we propose to answer all three questions by dividing existing operators into two main classes ( symmetrized vs. row-normalized spatial convolutions), and show how these translate into different implicit biases on the nature of the data. Finally, we show that this aggregation operator is in fact tunable, and explicit regimes in which certain choices of operators -- and therefore, embedding geometries -- might be more appropriate.

Deep Generative Modeling for Volume Reconstruction in Cryo-Electron Microscopy

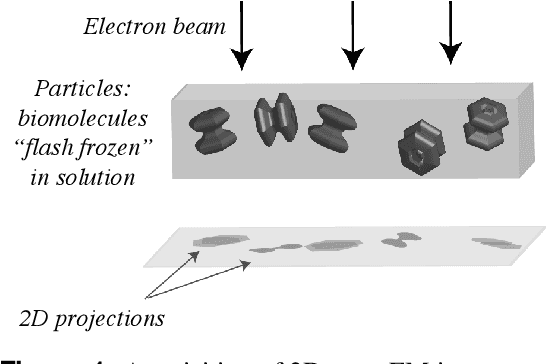
Recent breakthroughs in high resolution imaging of biomolecules in solution with cryo-electron microscopy (cryo-EM) have unlocked new doors for the reconstruction of molecular volumes, thereby promising further advances in biology, chemistry, and pharmacological research amongst others. Despite significant headway, the immense challenges in cryo-EM data analysis remain legion and intricately inter-disciplinary in nature, requiring insights from physicists, structural biologists, computer scientists, statisticians, and applied mathematicians. Meanwhile, recent next-generation volume reconstruction algorithms that combine generative modeling with end-to-end unsupervised deep learning techniques have shown promising results on simulated data, but still face considerable hurdles when applied to experimental cryo-EM images. In light of the proliferation of such methods and given the interdisciplinary nature of the task, we propose here a critical review of recent advances in the field of deep generative modeling for high resolution cryo-EM volume reconstruction. The present review aims to (i) compare and contrast these new methods, while (ii) presenting them from a perspective and using terminology familiar to scientists in each of the five aforementioned fields with no specific background in cryo-EM. The review begins with an introduction to the mathematical and computational challenges of deep generative models for cryo-EM volume reconstruction, along with an overview of the baseline methodology shared across this class of algorithms. Having established the common thread weaving through these different models, we provide a practical comparison of these state-of-the-art algorithms, highlighting their relative strengths and weaknesses, along with the assumptions that they rely on. This allows us to identify bottlenecks in current methods and avenues for future research.

Geomstats: A Python Package for Riemannian Geometry in Machine Learning

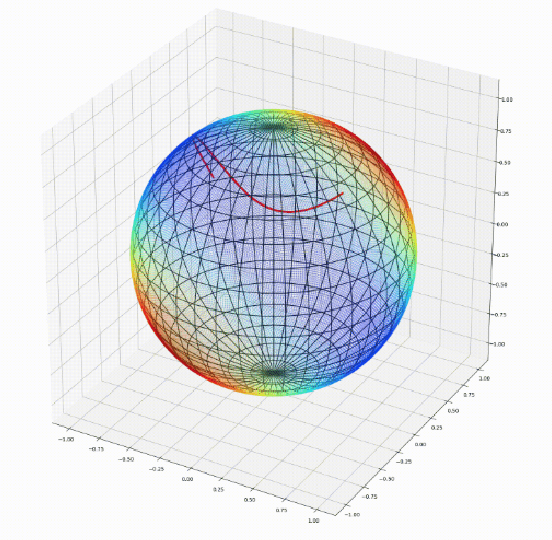
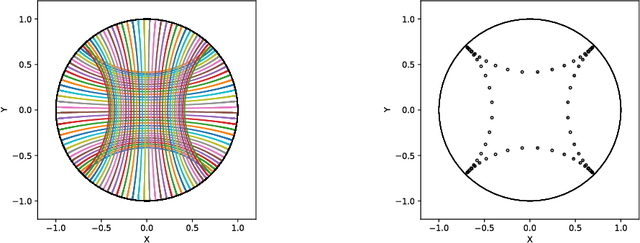
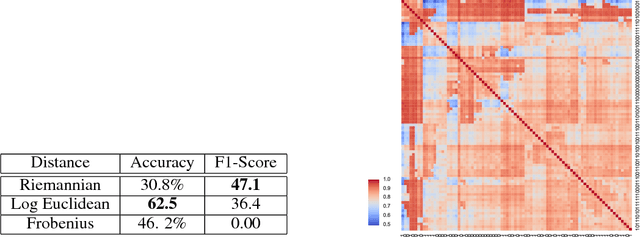
We introduce Geomstats, an open-source Python toolbox for computations and statistics on nonlinear manifolds, such as hyperbolic spaces, spaces of symmetric positive definite matrices, Lie groups of transformations, and many more. We provide object-oriented and extensively unit-tested implementations. Among others, manifolds come equipped with families of Riemannian metrics, with associated exponential and logarithmic maps, geodesics and parallel transport. Statistics and learning algorithms provide methods for estimation, clustering and dimension reduction on manifolds. All associated operations are vectorized for batch computation and provide support for different execution backends, namely NumPy, PyTorch and TensorFlow, enabling GPU acceleration. This paper presents the package, compares it with related libraries and provides relevant code examples. We show that Geomstats provides reliable building blocks to foster research in differential geometry and statistics, and to democratize the use of Riemannian geometry in machine learning applications. The source code is freely available under the MIT license at \url{geomstats.ai}.

Convex Hierarchical Clustering for Graph-Structured Data

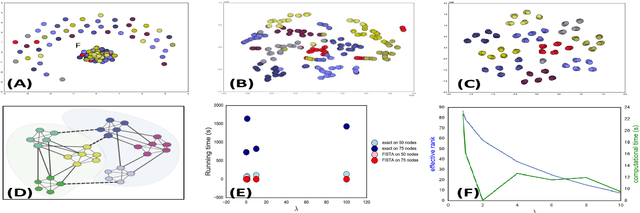
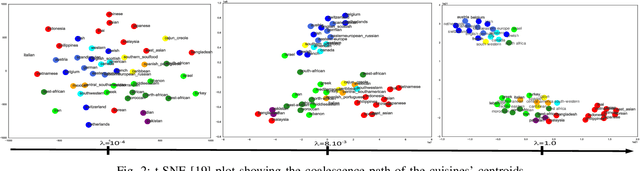
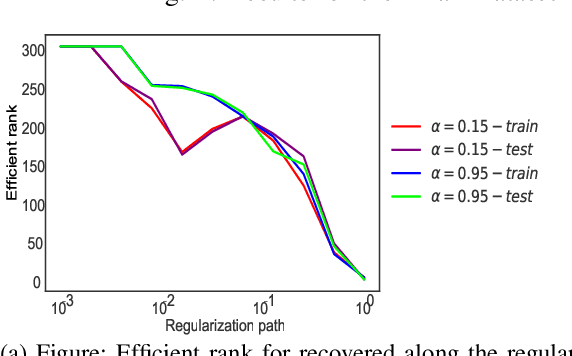
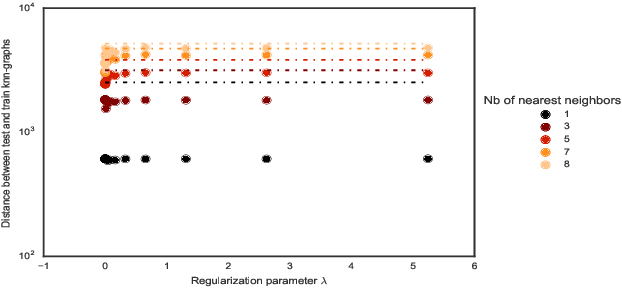
Convex clustering is a recent stable alternative to hierarchical clustering. It formulates the recovery of progressively coalescing clusters as a regularized convex problem. While convex clustering was originally designed for handling Euclidean distances between data points, in a growing number of applications, the data is directly characterized by a similarity matrix or weighted graph. In this paper, we extend the robust hierarchical clustering approach to these broader classes of similarities. Having defined an appropriate convex objective, the crux of this adaptation lies in our ability to provide: (a) an efficient recovery of the regularization path and (b) an empirical demonstration of the use of our method. We address the first challenge through a proximal dual algorithm, for which we characterize both the theoretical efficiency as well as the empirical performance on a set of experiments. Finally, we highlight the potential of our method by showing its application to several real-life datasets, thus providing a natural extension to the current scope of applications of convex clustering.

geomstats: a Python Package for Riemannian Geometry in Machine Learning

We introduce geomstats, a python package that performs computations on manifolds such as hyperspheres, hyperbolic spaces, spaces of symmetric positive definite matrices and Lie groups of transformations. We provide efficient and extensively unit-tested implementations of these manifolds, together with useful Riemannian metrics and associated Exponential and Logarithm maps. The corresponding geodesic distances provide a range of intuitive choices of Machine Learning loss functions. We also give the corresponding Riemannian gradients. The operations implemented in geomstats are available with different computing backends such as numpy, tensorflow and keras. We have enabled GPU implementation and integrated geomstats manifold computations into keras deep learning framework. This paper also presents a review of manifolds in machine learning and an overview of the geomstats package with examples demonstrating its use for efficient and user-friendly Riemannian geometry.