Understanding the Effect of GCN Convolutions in Regression Tasks
Paper and Code
Oct 26, 2024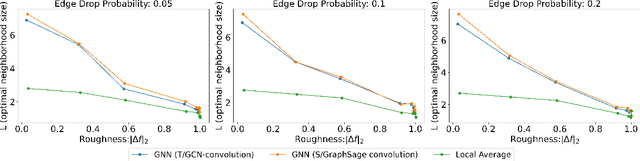
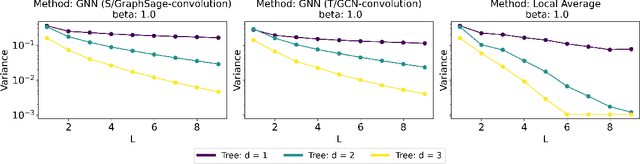
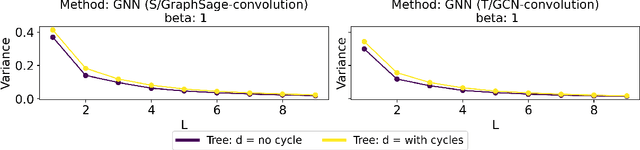
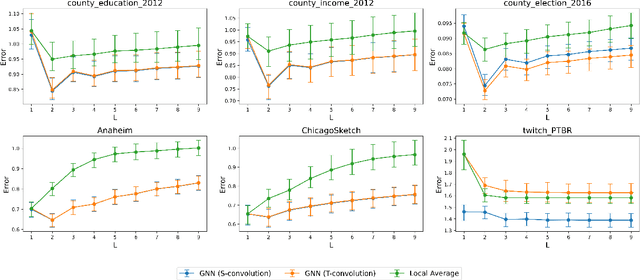
Graph Convolutional Networks (GCNs) have become a pivotal method in machine learning for modeling functions over graphs. Despite their widespread success across various applications, their statistical properties (e.g. consistency, convergence rates) remain ill-characterized. To begin addressing this knowledge gap, in this paper, we provide a formal analysis of the impact of convolution operators on regression tasks over homophilic networks. Focusing on estimators based solely on neighborhood aggregation, we examine how two common convolutions - the original GCN and GraphSage convolutions - affect the learning error as a function of the neighborhood topology and the number of convolutional layers. We explicitly characterize the bias-variance trade-off incurred by GCNs as a function of the neighborhood size and identify specific graph topologies where convolution operators are less effective. Our theoretical findings are corroborated by synthetic experiments, and provide a start to a deeper quantitative understanding of convolutional effects in GCNs for offering rigorous guidelines for practitioners.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge