Improving the Convergence Rates of Forward Gradient Descent with Repeated Sampling

Forward gradient descent (FGD) has been proposed as a biologically more plausible alternative of gradient descent as it can be computed without backward pass. Considering the linear model with $d$ parameters, previous work has found that the prediction error of FGD is, however, by a factor $d$ slower than the prediction error of stochastic gradient descent (SGD). In this paper we show that by computing $\ell$ FGD steps based on each training sample, this suboptimality factor becomes $d/(\ell \wedge d)$ and thus the suboptimality of the rate disappears if $\ell \gtrsim d.$ We also show that FGD with repeated sampling can adapt to low-dimensional structure in the input distribution. The main mathematical challenge lies in controlling the dependencies arising from the repeated sampling process.

Understanding the Effect of GCN Convolutions in Regression Tasks

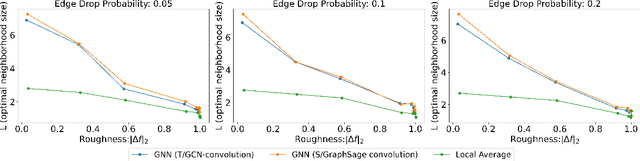
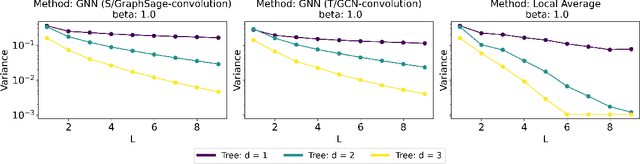
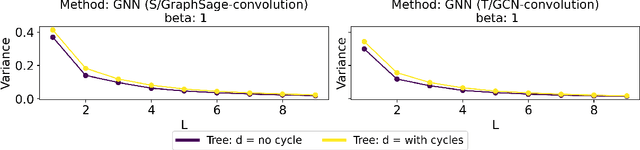
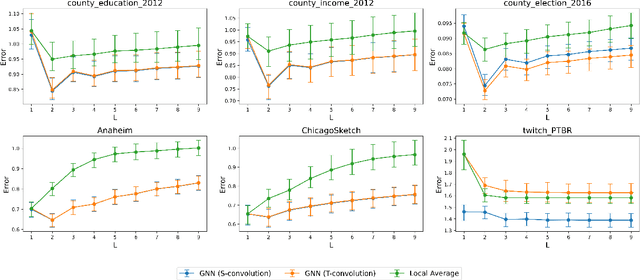
Graph Convolutional Networks (GCNs) have become a pivotal method in machine learning for modeling functions over graphs. Despite their widespread success across various applications, their statistical properties (e.g. consistency, convergence rates) remain ill-characterized. To begin addressing this knowledge gap, in this paper, we provide a formal analysis of the impact of convolution operators on regression tasks over homophilic networks. Focusing on estimators based solely on neighborhood aggregation, we examine how two common convolutions - the original GCN and GraphSage convolutions - affect the learning error as a function of the neighborhood topology and the number of convolutional layers. We explicitly characterize the bias-variance trade-off incurred by GCNs as a function of the neighborhood size and identify specific graph topologies where convolution operators are less effective. Our theoretical findings are corroborated by synthetic experiments, and provide a start to a deeper quantitative understanding of convolutional effects in GCNs for offering rigorous guidelines for practitioners.

On the VC dimension of deep group convolutional neural networks

We study the generalization capabilities of Group Convolutional Neural Networks (GCNNs) with ReLU activation function by deriving upper and lower bounds for their Vapnik-Chervonenkis (VC) dimension. Specifically, we analyze how factors such as the number of layers, weights, and input dimension affect the VC dimension. We further compare the derived bounds to those known for other types of neural networks. Our findings extend previous results on the VC dimension of continuous GCNNs with two layers, thereby providing new insights into the generalization properties of GCNNs, particularly regarding the dependence on the input resolution of the data.

Asymptotics of Stochastic Gradient Descent with Dropout Regularization in Linear Models

This paper proposes an asymptotic theory for online inference of the stochastic gradient descent (SGD) iterates with dropout regularization in linear regression. Specifically, we establish the geometric-moment contraction (GMC) for constant step-size SGD dropout iterates to show the existence of a unique stationary distribution of the dropout recursive function. By the GMC property, we provide quenched central limit theorems (CLT) for the difference between dropout and $\ell^2$-regularized iterates, regardless of initialization. The CLT for the difference between the Ruppert-Polyak averaged SGD (ASGD) with dropout and $\ell^2$-regularized iterates is also presented. Based on these asymptotic normality results, we further introduce an online estimator for the long-run covariance matrix of ASGD dropout to facilitate inference in a recursive manner with efficiency in computational time and memory. The numerical experiments demonstrate that for sufficiently large samples, the proposed confidence intervals for ASGD with dropout nearly achieve the nominal coverage probability.

Convergence guarantees for forward gradient descent in the linear regression model

Renewed interest in the relationship between artificial and biological neural networks motivates the study of gradient-free methods. Considering the linear regression model with random design, we theoretically analyze in this work the biologically motivated (weight-perturbed) forward gradient scheme that is based on random linear combination of the gradient. If d denotes the number of parameters and k the number of samples, we prove that the mean squared error of this method converges for $k\gtrsim d^2\log(d)$ with rate $d^2\log(d)/k.$ Compared to the dimension dependence d for stochastic gradient descent, an additional factor $d\log(d)$ occurs.

Dropout Regularization Versus $\ell_2$-Penalization in the Linear Model

We investigate the statistical behavior of gradient descent iterates with dropout in the linear regression model. In particular, non-asymptotic bounds for expectations and covariance matrices of the iterates are derived. In contrast with the widely cited connection between dropout and $\ell_2$-regularization in expectation, the results indicate a much more subtle relationship, owing to interactions between the gradient descent dynamics and the additional randomness induced by dropout. We also study a simplified variant of dropout which does not have a regularizing effect and converges to the least squares estimator.

Interpreting learning in biological neural networks as zero-order optimization method

Recently, significant progress has been made regarding the statistical understanding of artificial neural networks (ANNs). ANNs are motivated by the functioning of the brain, but differ in several crucial aspects. In particular, it is biologically implausible that the learning of the brain is based on gradient descent. In this work we look at the brain as a statistical method for supervised learning. The main contribution is to relate the local updating rule of the connection parameters in biological neural networks (BNNs) to a zero-order optimization method.

On the inability of Gaussian process regression to optimally learn compositional functions

We rigorously prove that deep Gaussian process priors can outperform Gaussian process priors if the target function has a compositional structure. To this end, we study information-theoretic lower bounds for posterior contraction rates for Gaussian process regression in a continuous regression model. We show that if the true function is a generalized additive function, then the posterior based on any mean-zero Gaussian process can only recover the truth at a rate that is strictly slower than the minimax rate by a factor that is polynomially suboptimal in the sample size $n$.

On generalization bounds for deep networks based on loss surface implicit regularization

The classical statistical learning theory says that fitting too many parameters leads to overfitting and poor performance. That modern deep neural networks generalize well despite a large number of parameters contradicts this finding and constitutes a major unsolved problem towards explaining the success of deep learning. The implicit regularization induced by stochastic gradient descent (SGD) has been regarded to be important, but its specific principle is still unknown. In this work, we study how the local geometry of the energy landscape around local minima affects the statistical properties of SGD with Gaussian gradient noise. We argue that under reasonable assumptions, the local geometry forces SGD to stay close to a low dimensional subspace and that this induces implicit regularization and results in tighter bounds on the generalization error for deep neural networks. To derive generalization error bounds for neural networks, we first introduce a notion of stagnation sets around the local minima and impose a local essential convexity property of the population risk. Under these conditions, lower bounds for SGD to remain in these stagnation sets are derived. If stagnation occurs, we derive a bound on the generalization error of deep neural networks involving the spectral norms of the weight matrices but not the number of network parameters. Technically, our proofs are based on controlling the change of parameter values in the SGD iterates and local uniform convergence of the empirical loss functions based on the entropy of suitable neighborhoods around local minima. Our work attempts to better connect non-convex optimization and generalization analysis with uniform convergence.

Convergence rates of deep ReLU networks for multiclass classification

For classification problems, trained deep neural networks return probabilities of class memberships. In this work we study convergence of the learned probabilities to the true conditional class probabilities. More specifically we consider sparse deep ReLU network reconstructions minimizing cross-entropy loss in the multiclass classification setup. Interesting phenomena occur when the class membership probabilities are close to zero. Convergence rates are derived that depend on the near-zero behaviour via a margin-type condition.