Sophie Langer
On the expressivity of deep Heaviside networks
Apr 30, 2025



Abstract:We show that deep Heaviside networks (DHNs) have limited expressiveness but that this can be overcome by including either skip connections or neurons with linear activation. We provide lower and upper bounds for the Vapnik-Chervonenkis (VC) dimensions and approximation rates of these network classes. As an application, we derive statistical convergence rates for DHN fits in the nonparametric regression model.
Training Diagonal Linear Networks with Stochastic Sharpness-Aware Minimization
Mar 14, 2025Abstract:We analyze the landscape and training dynamics of diagonal linear networks in a linear regression task, with the network parameters being perturbed by small isotropic normal noise. The addition of such noise may be interpreted as a stochastic form of sharpness-aware minimization (SAM) and we prove several results that relate its action on the underlying landscape and training dynamics to the sharpness of the loss. In particular, the noise changes the expected gradient to force balancing of the weight matrices at a fast rate along the descent trajectory. In the diagonal linear model, we show that this equates to minimizing the average sharpness, as well as the trace of the Hessian matrix, among all possible factorizations of the same matrix. Further, the noise forces the gradient descent iterates towards a shrinkage-thresholding of the underlying true parameter, with the noise level explicitly regulating both the shrinkage factor and the threshold.
On the VC dimension of deep group convolutional neural networks
Oct 21, 2024Abstract:We study the generalization capabilities of Group Convolutional Neural Networks (GCNNs) with ReLU activation function by deriving upper and lower bounds for their Vapnik-Chervonenkis (VC) dimension. Specifically, we analyze how factors such as the number of layers, weights, and input dimension affect the VC dimension. We further compare the derived bounds to those known for other types of neural networks. Our findings extend previous results on the VC dimension of continuous GCNNs with two layers, thereby providing new insights into the generalization properties of GCNNs, particularly regarding the dependence on the input resolution of the data.
Learning Green's Function Efficiently Using Low-Rank Approximations
Aug 01, 2023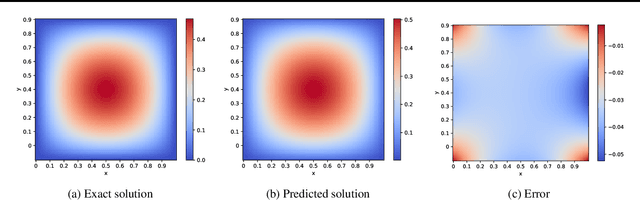


Abstract:Learning the Green's function using deep learning models enables to solve different classes of partial differential equations. A practical limitation of using deep learning for the Green's function is the repeated computationally expensive Monte-Carlo integral approximations. We propose to learn the Green's function by low-rank decomposition, which results in a novel architecture to remove redundant computations by separate learning with domain data for evaluation and Monte-Carlo samples for integral approximation. Using experiments we show that the proposed method improves computational time compared to MOD-Net while achieving comparable accuracy compared to both PINNs and MOD-Net.
Dropout Regularization Versus $\ell_2$-Penalization in the Linear Model
Jun 18, 2023Abstract:We investigate the statistical behavior of gradient descent iterates with dropout in the linear regression model. In particular, non-asymptotic bounds for expectations and covariance matrices of the iterates are derived. In contrast with the widely cited connection between dropout and $\ell_2$-regularization in expectation, the results indicate a much more subtle relationship, owing to interactions between the gradient descent dynamics and the additional randomness induced by dropout. We also study a simplified variant of dropout which does not have a regularizing effect and converges to the least squares estimator.
Estimation of a regression function on a manifold by fully connected deep neural networks
Jul 20, 2021Abstract:Estimation of a regression function from independent and identically distributed data is considered. The $L_2$ error with integration with respect to the distribution of the predictor variable is used as the error criterion. The rate of convergence of least squares estimates based on fully connected spaces of deep neural networks with ReLU activation function is analyzed for smooth regression functions. It is shown that in case that the distribution of the predictor variable is concentrated on a manifold, these estimates achieve a rate of convergence which depends on the dimension of the manifold and not on the number of components of the predictor variable.
Approximating smooth functions by deep neural networks with sigmoid activation function
Oct 08, 2020
Abstract:We study the power of deep neural networks (DNNs) with sigmoid activation function. Recently, it was shown that DNNs approximate any $d$-dimensional, smooth function on a compact set with a rate of order $W^{-p/d}$, where $W$ is the number of nonzero weights in the network and $p$ is the smoothness of the function. Unfortunately, these rates only hold for a special class of sparsely connected DNNs. We ask ourselves if we can show the same approximation rate for a simpler and more general class, i.e., DNNs which are only defined by its width and depth. In this article we show that DNNs with fixed depth and a width of order $M^d$ achieve an approximation rate of $M^{-2p}$. As a conclusion we quantitatively characterize the approximation power of DNNs in terms of the overall weights $W_0$ in the network and show an approximation rate of $W_0^{-p/d}$. This more general result finally helps us to understand which network topology guarantees a special target accuracy.
Deep Learning and MARS: A Connection
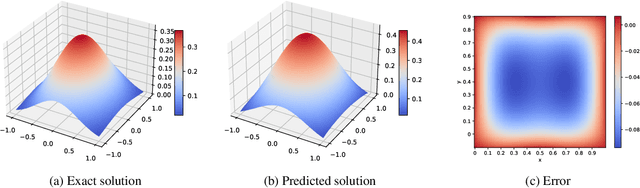
Sep 08, 2019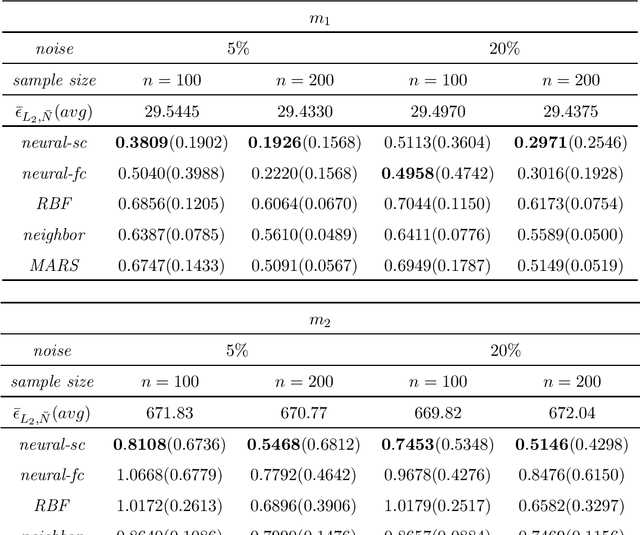
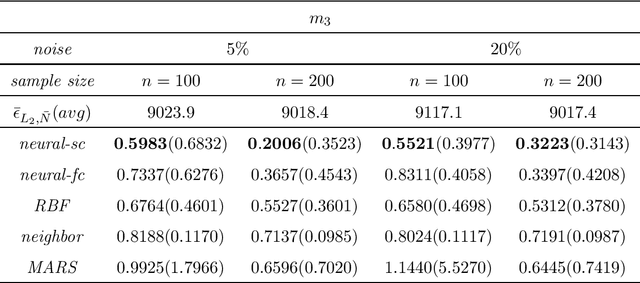

Abstract:We consider least squares regression estimates using deep neural networks. We show that these estimates satisfy an oracle inequality, which implies that (up to a logarithmic factor) the error of these estimates is at least as small as the optimal possible error bound which one would expect for MARS in case that this procedure would work in the optimal way. As a result we show that our neural networks are able to achieve a dimensionality reduction in case that the regression function locally has low dimensionality. This assumption seems to be realistic in real-world applications, since selected high-dimensional data are often confined to locally-low-dimensional distributions. In our simulation study we provide numerical experiments to support our theoretical results and to compare our estimate with other conventional nonparametric regression estimates, especially with MARS. The use of our estimates is illustrated through a real data analysis.
On the rate of convergence of fully connected very deep neural network regression estimates
Aug 29, 2019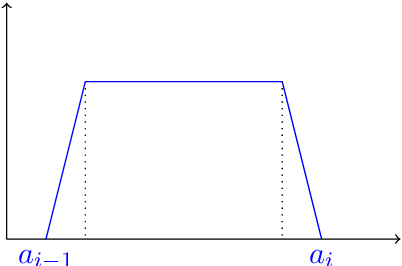
Abstract:Recent results in nonparametric regression show that deep learning, i.e., neural networks estimates with many hidden layers, are able to circumvent the so-called curse of dimensionality in case that suitable restrictions on the structure of the regression function hold. One key feature of the neural networks used in these results is that they are not fully connected. In this paper we show that we can get similar results also for fully connected multilayer feedforward neural networks with ReLU activation functions, provided the number of neurons per hidden layer is fixed and the number of hidden layers tends to infinity for sample size tending to infinity. The proof is based on new approximation results concerning fully connected deep neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge