Learning Green's Function Efficiently Using Low-Rank Approximations

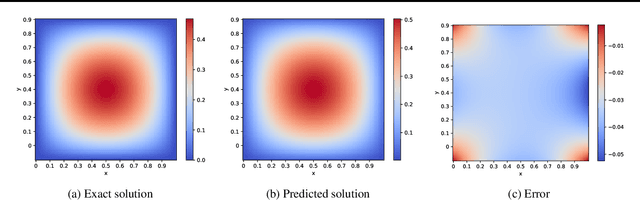
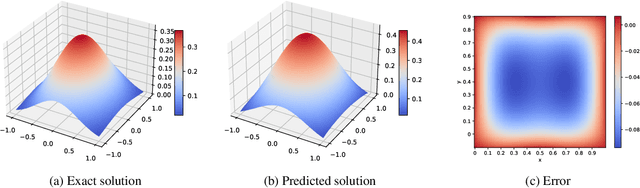
Learning the Green's function using deep learning models enables to solve different classes of partial differential equations. A practical limitation of using deep learning for the Green's function is the repeated computationally expensive Monte-Carlo integral approximations. We propose to learn the Green's function by low-rank decomposition, which results in a novel architecture to remove redundant computations by separate learning with domain data for evaluation and Monte-Carlo samples for integral approximation. Using experiments we show that the proposed method improves computational time compared to MOD-Net while achieving comparable accuracy compared to both PINNs and MOD-Net.

Graph Polynomial Convolution Models for Node Classification of Non-Homophilous Graphs

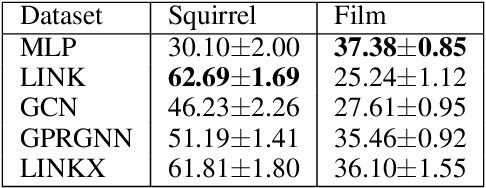
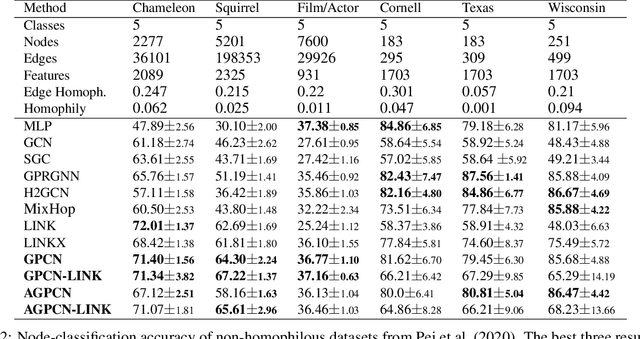
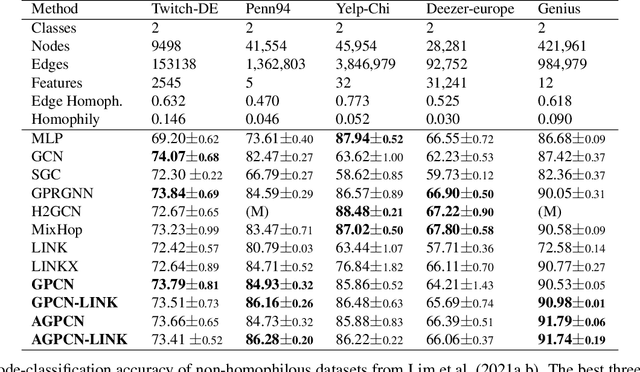
We investigate efficient learning from higher-order graph convolution and learning directly from adjacency matrices for node classification. We revisit the scaled graph residual network and remove ReLU activation from residual layers and apply a single weight matrix at each residual layer. We show that the resulting model lead to new graph convolution models as a polynomial of the normalized adjacency matrix, the residual weight matrix, and the residual scaling parameter. Additionally, we propose adaptive learning between directly graph polynomial convolution models and learning directly from the adjacency matrix. Furthermore, we propose fully adaptive models to learn scaling parameters at each residual layer. We show that generalization bounds of proposed methods are bounded as a polynomial of eigenvalue spectrum, scaling parameters, and upper bounds of residual weights. By theoretical analysis, we argue that the proposed models can obtain improved generalization bounds by limiting the higher-orders of convolutions and direct learning from the adjacency matrix. Using a wide set of real-data, we demonstrate that the proposed methods obtain improved accuracy for node-classification of non-homophilous graphs.

Adaptive and Interpretable Graph Convolution Networks Using Generalized Pagerank

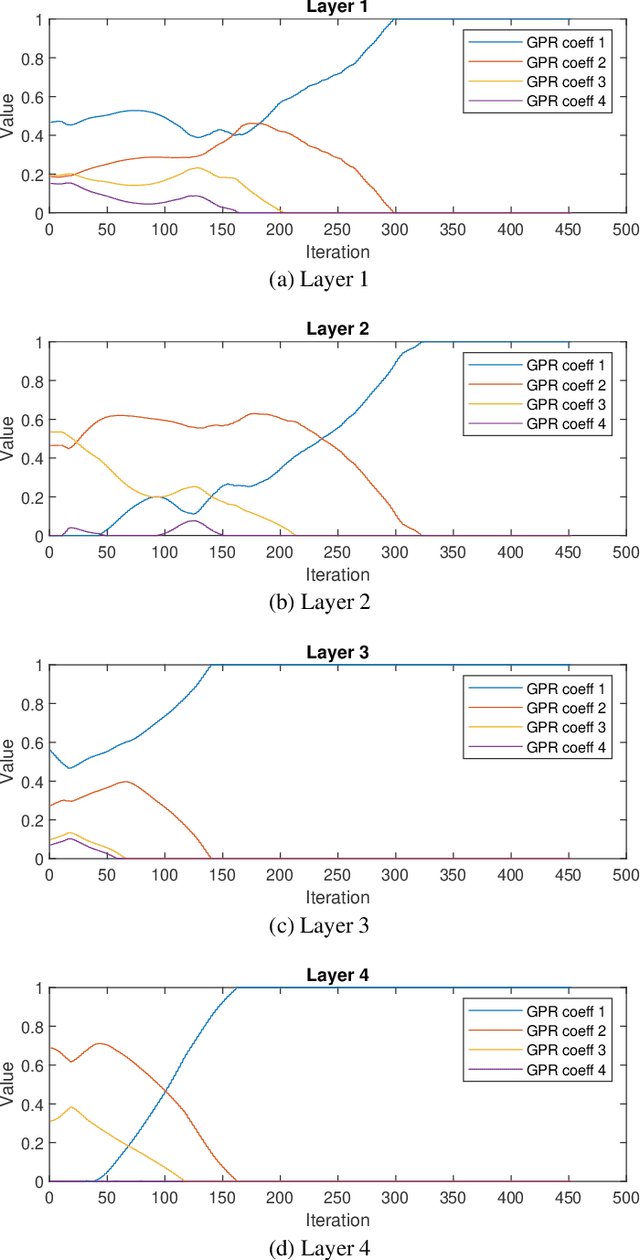
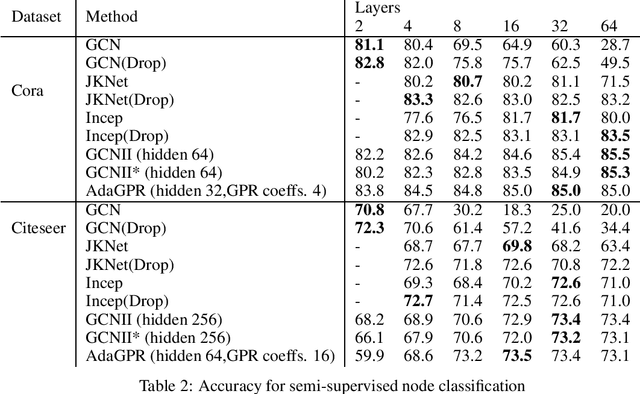
We investigate adaptive layer-wise graph convolution in deep GCN models. We propose AdaGPR to learn generalized Pageranks at each layer of a GCNII network to induce adaptive convolution. We show that the generalization bound for AdaGPR is bounded by a polynomial of the eigenvalue spectrum of the normalized adjacency matrix in the order of the number of generalized Pagerank coefficients. By analysing the generalization bounds we show that oversmoothing depends on both the convolutions by the higher orders of the normalized adjacency matrix and the depth of the model. We performed evaluations on node-classification using benchmark real data and show that AdaGPR provides improved accuracies compared to existing graph convolution networks while demonstrating robustness against oversmoothing. Further, we demonstrate that analysis of coefficients of layer-wise generalized Pageranks allows us to qualitatively understand convolution at each layer enabling model interpretations.

Convex Coupled Matrix and Tensor Completion

We propose a set of convex low rank inducing norms for a coupled matrices and tensors (hereafter coupled tensors), which shares information between matrices and tensors through common modes. More specifically, we propose a mixture of the overlapped trace norm and the latent norms with the matrix trace norm, and then, we propose a new completion algorithm based on the proposed norms. A key advantage of the proposed norms is that it is convex and can find a globally optimal solution, while existing methods for coupled learning are non-convex. Furthermore, we analyze the excess risk bounds of the completion model regularized by our proposed norms which show that our proposed norms can exploit the low rankness of coupled tensors leading to better bounds compared to uncoupled norms. Through synthetic and real-world data experiments, we show that the proposed completion algorithm compares favorably with existing completion algorithms.

Convex Factorization Machine for Regression

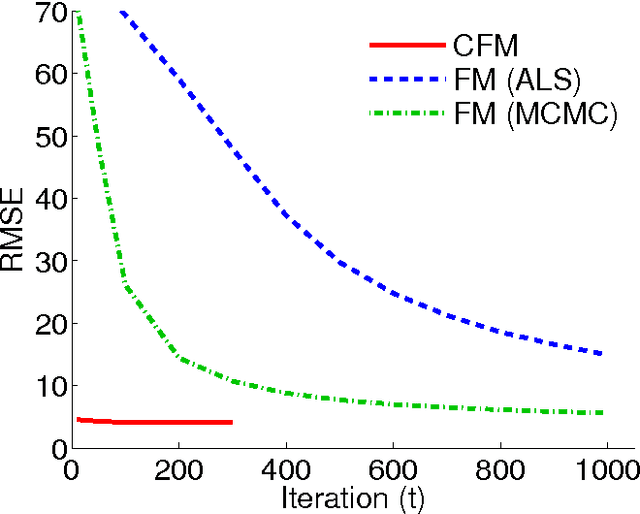
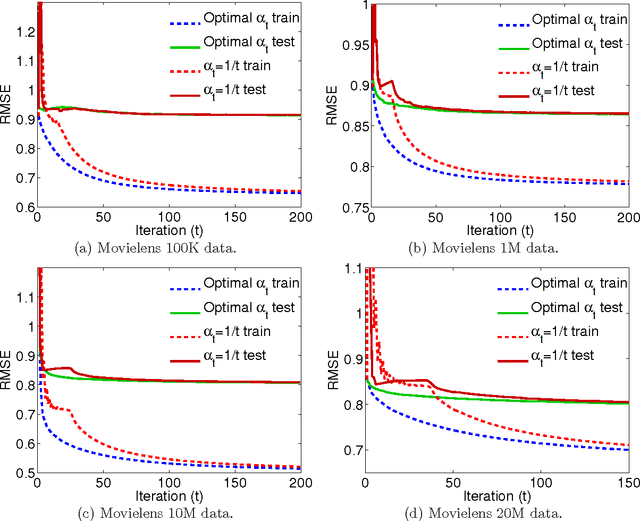
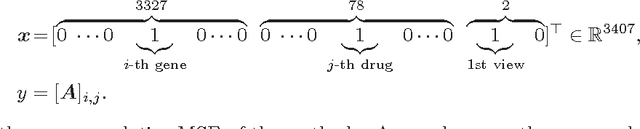
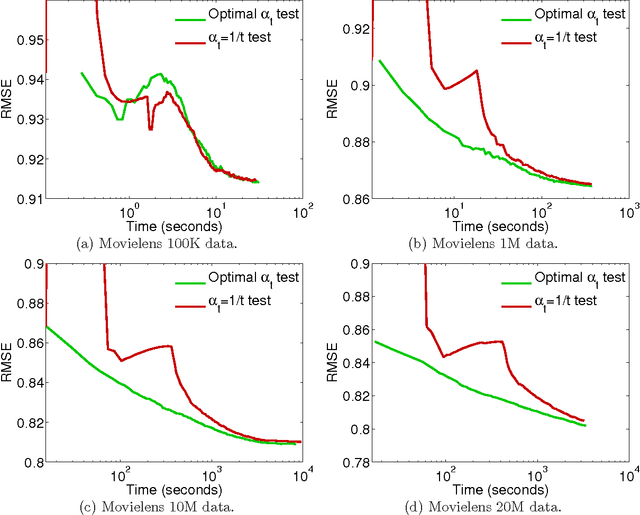
We propose the convex factorization machine (CFM), which is a convex variant of the widely used Factorization Machines (FMs). Specifically, we employ a linear+quadratic model and regularize the linear term with the $\ell_2$-regularizer and the quadratic term with the trace norm regularizer. Then, we formulate the CFM optimization as a semidefinite programming problem and propose an efficient optimization procedure with Hazan's algorithm. A key advantage of CFM over existing FMs is that it can find a globally optimal solution, while FMs may get a poor locally optimal solution since the objective function of FMs is non-convex. In addition, the proposed algorithm is simple yet effective and can be implemented easily. Finally, CFM is a general factorization method and can also be used for other factorization problems including including multi-view matrix factorization and tensor completion problems. Through synthetic and movielens datasets, we first show that the proposed CFM achieves results competitive to FMs. Furthermore, in a toxicogenomics prediction task, we show that CFM outperforms a state-of-the-art tensor factorization method.

Theoretical and Experimental Analyses of Tensor-Based Regression and Classification

We theoretically and experimentally investigate tensor-based regression and classification. Our focus is regularization with various tensor norms, including the overlapped trace norm, the latent trace norm, and the scaled latent trace norm. We first give dual optimization methods using the alternating direction method of multipliers, which is computationally efficient when the number of training samples is moderate. We then theoretically derive an excess risk bound for each tensor norm and clarify their behavior. Finally, we perform extensive experiments using simulated and real data and demonstrate the superiority of tensor-based learning methods over vector- and matrix-based learning methods.