Physics-based reward driven image analysis in microscopy

The rise of electron microscopy has expanded our ability to acquire nanometer and atomically resolved images of complex materials. The resulting vast datasets are typically analyzed by human operators, an intrinsically challenging process due to the multiple possible analysis steps and the corresponding need to build and optimize complex analysis workflows. We present a methodology based on the concept of a Reward Function coupled with Bayesian Optimization, to optimize image analysis workflows dynamically. The Reward Function is engineered to closely align with the experimental objectives and broader context and is quantifiable upon completion of the analysis. Here, cross-section, high-angle annular dark field (HAADF) images of ion-irradiated $(Y, Dy)Ba_2Cu_3O_{7-\delta}$ thin-films were used as a model system. The reward functions were formed based on the expected materials density and atomic spacings and used to drive multi-objective optimization of the classical Laplacian-of-Gaussian (LoG) method. These results can be benchmarked against the DCNN segmentation. This optimized LoG* compares favorably against DCNN in the presence of the additional noise. We further extend the reward function approach towards the identification of partially-disordered regions, creating a physics-driven reward function and action space of high-dimensional clustering. We pose that with correct definition, the reward function approach allows real-time optimization of complex analysis workflows at much higher speeds and lower computational costs than classical DCNN-based inference, ensuring the attainment of results that are both precise and aligned with the human-defined objectives.

Convex Factorization Machine for Regression

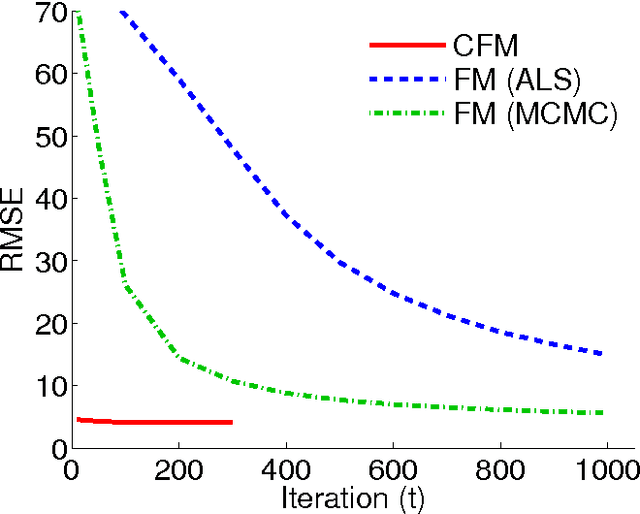
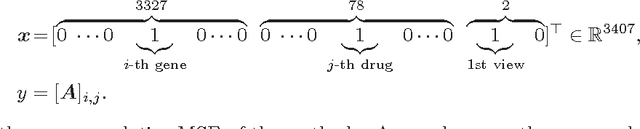
We propose the convex factorization machine (CFM), which is a convex variant of the widely used Factorization Machines (FMs). Specifically, we employ a linear+quadratic model and regularize the linear term with the $\ell_2$-regularizer and the quadratic term with the trace norm regularizer. Then, we formulate the CFM optimization as a semidefinite programming problem and propose an efficient optimization procedure with Hazan's algorithm. A key advantage of CFM over existing FMs is that it can find a globally optimal solution, while FMs may get a poor locally optimal solution since the objective function of FMs is non-convex. In addition, the proposed algorithm is simple yet effective and can be implemented easily. Finally, CFM is a general factorization method and can also be used for other factorization problems including including multi-view matrix factorization and tensor completion problems. Through synthetic and movielens datasets, we first show that the proposed CFM achieves results competitive to FMs. Furthermore, in a toxicogenomics prediction task, we show that CFM outperforms a state-of-the-art tensor factorization method.