Learning Green's Function Efficiently Using Low-Rank Approximations
Paper and Code
Aug 01, 2023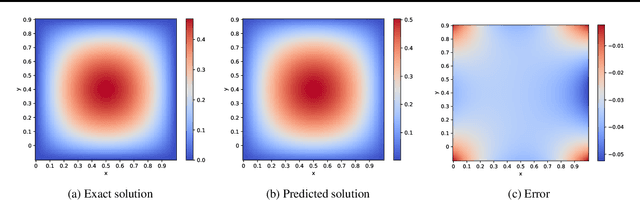

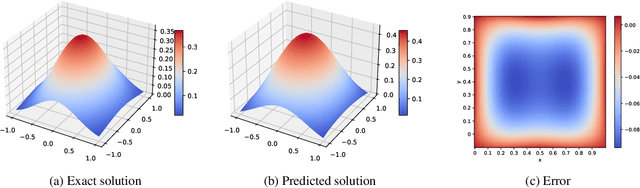

Learning the Green's function using deep learning models enables to solve different classes of partial differential equations. A practical limitation of using deep learning for the Green's function is the repeated computationally expensive Monte-Carlo integral approximations. We propose to learn the Green's function by low-rank decomposition, which results in a novel architecture to remove redundant computations by separate learning with domain data for evaluation and Monte-Carlo samples for integral approximation. Using experiments we show that the proposed method improves computational time compared to MOD-Net while achieving comparable accuracy compared to both PINNs and MOD-Net.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge