Analysis of the rate of convergence of an over-parametrized convolutional neural network image classifier learned by gradient descent

Image classification based on over-parametrized convolutional neural networks with a global average-pooling layer is considered. The weights of the network are learned by gradient descent. A bound on the rate of convergence of the difference between the misclassification risk of the newly introduced convolutional neural network estimate and the minimal possible value is derived.

On the rate of convergence of an over-parametrized Transformer classifier learned by gradient descent

One of the most recent and fascinating breakthroughs in artificial intelligence is ChatGPT, a chatbot which can simulate human conversation. ChatGPT is an instance of GPT4, which is a language model based on generative gredictive gransformers. So if one wants to study from a theoretical point of view, how powerful such artificial intelligence can be, one approach is to consider transformer networks and to study which problems one can solve with these networks theoretically. Here it is not only important what kind of models these network can approximate, or how they can generalize their knowledge learned by choosing the best possible approximation to a concrete data set, but also how well optimization of such transformer network based on concrete data set works. In this article we consider all these three different aspects simultaneously and show a theoretical upper bound on the missclassification probability of a transformer network fitted to the observed data. For simplicity we focus in this context on transformer encoder networks which can be applied to define an estimate in the context of a classification problem involving natural language.

Analysis of the expected $L_2$ error of an over-parametrized deep neural network estimate learned by gradient descent without regularization

Recent results show that estimates defined by over-parametrized deep neural networks learned by applying gradient descent to a regularized empirical $L_2$ risk are universally consistent and achieve good rates of convergence. In this paper, we show that the regularization term is not necessary to obtain similar results. In the case of a suitably chosen initialization of the network, a suitable number of gradient descent steps, and a suitable step size we show that an estimate without a regularization term is universally consistent for bounded predictor variables. Additionally, we show that if the regression function is H\"older smooth with H\"older exponent $1/2 \leq p \leq 1$, the $L_2$ error converges to zero with a convergence rate of approximately $n^{-1/(1+d)}$. Furthermore, in case of an interaction model, where the regression function consists of a sum of H\"older smooth functions with $d^*$ components, a rate of convergence is derived which does not depend on the input dimension $d$.

Analysis of convolutional neural network image classifiers in a rotationally symmetric model

Convolutional neural network image classifiers are defined and the rate of convergence of the misclassification risk of the estimates towards the optimal misclassification risk is analyzed. Here we consider images as random variables with values in some functional space, where we only observe discrete samples as function values on some finite grid. Under suitable structural and smoothness assumptions on the functional a posteriori probability, which includes some kind of symmetry against rotation of subparts of the input image, it is shown that least squares plug-in classifiers based on convolutional neural networks are able to circumvent the curse of dimensionality in binary image classification if we neglect a resolution-dependent error term. The finite sample size behavior of the classifier is analyzed by applying it to simulated and real data.

On the rate of convergence of a classifier based on a Transformer encoder

Pattern recognition based on a high-dimensional predictor is considered. A classifier is defined which is based on a Transformer encoder. The rate of convergence of the misclassification probability of the classifier towards the optimal misclassification probability is analyzed. It is shown that this classifier is able to circumvent the curse of dimensionality provided the aposteriori probability satisfies a suitable hierarchical composition model. Furthermore, the difference between Transformer classifiers analyzed theoretically in this paper and Transformer classifiers used nowadays in practice are illustrated by considering classification problems in natural language processing.

Estimation of a regression function on a manifold by fully connected deep neural networks

Estimation of a regression function from independent and identically distributed data is considered. The $L_2$ error with integration with respect to the distribution of the predictor variable is used as the error criterion. The rate of convergence of least squares estimates based on fully connected spaces of deep neural networks with ReLU activation function is analyzed for smooth regression functions. It is shown that in case that the distribution of the predictor variable is concentrated on a manifold, these estimates achieve a rate of convergence which depends on the dimension of the manifold and not on the number of components of the predictor variable.

On the rate of convergence of a deep recurrent neural network estimate in a regression problem with dependent data

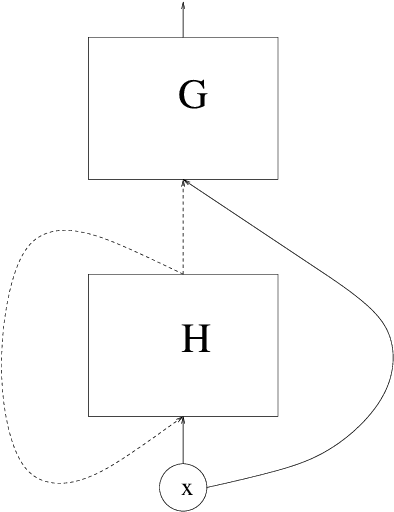
A regression problem with dependent data is considered. Regularity assumptions on the dependency of the data are introduced, and it is shown that under suitable structural assumptions on the regression function a deep recurrent neural network estimate is able to circumvent the curse of dimensionality.

Common Voice: A Massively-Multilingual Speech Corpus

The Common Voice corpus is a massively-multilingual collection of transcribed speech intended for speech technology research and development. Common Voice is designed for Automatic Speech Recognition purposes but can be useful in other domains (e.g. language identification). To achieve scale and sustainability, the Common Voice project employs crowdsourcing for both data collection and data validation. The most recent release includes 29 languages, and as of November 2019 there are a total of 38 languages collecting data. Over 50,000 individuals have participated so far, resulting in 2,500 hours of collected audio. To our knowledge this is the largest audio corpus in the public domain for speech recognition, both in terms of number of hours and number of languages. As an example use case for Common Voice, we present speech recognition experiments using Mozilla's DeepSpeech Speech-to-Text toolkit. By applying transfer learning from a source English model, we find an average Character Error Rate improvement of 5.99 +/- 5.48 for twelve target languages (German, French, Italian, Turkish, Catalan, Slovenian, Welsh, Irish, Breton, Tatar, Chuvash, and Kabyle). For most of these languages, these are the first ever published results on end-to-end Automatic Speech Recognition.

Deep Learning and MARS: A Connection

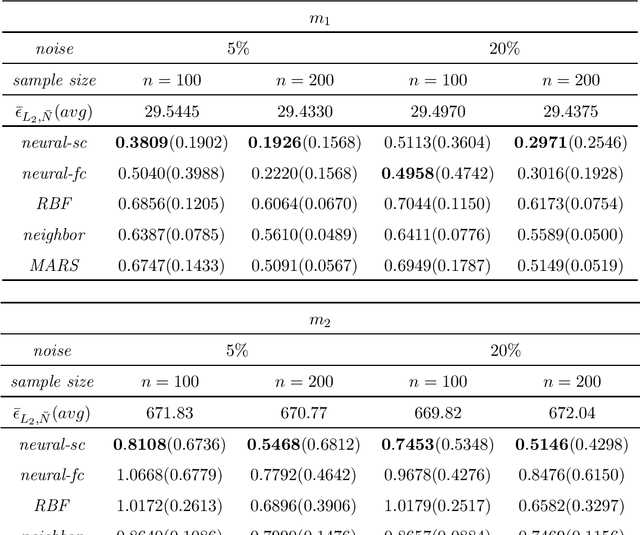
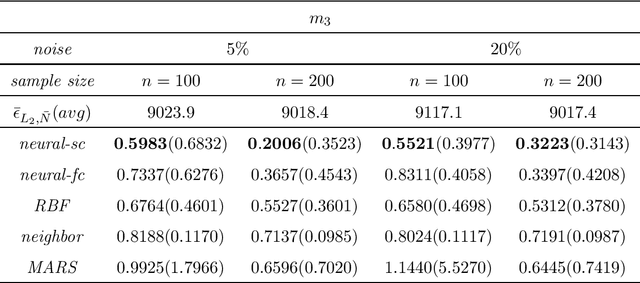
We consider least squares regression estimates using deep neural networks. We show that these estimates satisfy an oracle inequality, which implies that (up to a logarithmic factor) the error of these estimates is at least as small as the optimal possible error bound which one would expect for MARS in case that this procedure would work in the optimal way. As a result we show that our neural networks are able to achieve a dimensionality reduction in case that the regression function locally has low dimensionality. This assumption seems to be realistic in real-world applications, since selected high-dimensional data are often confined to locally-low-dimensional distributions. In our simulation study we provide numerical experiments to support our theoretical results and to compare our estimate with other conventional nonparametric regression estimates, especially with MARS. The use of our estimates is illustrated through a real data analysis.

On the rate of convergence of fully connected very deep neural network regression estimates

Recent results in nonparametric regression show that deep learning, i.e., neural networks estimates with many hidden layers, are able to circumvent the so-called curse of dimensionality in case that suitable restrictions on the structure of the regression function hold. One key feature of the neural networks used in these results is that they are not fully connected. In this paper we show that we can get similar results also for fully connected multilayer feedforward neural networks with ReLU activation functions, provided the number of neurons per hidden layer is fixed and the number of hidden layers tends to infinity for sample size tending to infinity. The proof is based on new approximation results concerning fully connected deep neural networks.