Training Diagonal Linear Networks with Stochastic Sharpness-Aware Minimization

We analyze the landscape and training dynamics of diagonal linear networks in a linear regression task, with the network parameters being perturbed by small isotropic normal noise. The addition of such noise may be interpreted as a stochastic form of sharpness-aware minimization (SAM) and we prove several results that relate its action on the underlying landscape and training dynamics to the sharpness of the loss. In particular, the noise changes the expected gradient to force balancing of the weight matrices at a fast rate along the descent trajectory. In the diagonal linear model, we show that this equates to minimizing the average sharpness, as well as the trace of the Hessian matrix, among all possible factorizations of the same matrix. Further, the noise forces the gradient descent iterates towards a shrinkage-thresholding of the underlying true parameter, with the noise level explicitly regulating both the shrinkage factor and the threshold.

Dropout Regularization Versus $\ell_2$-Penalization in the Linear Model

We investigate the statistical behavior of gradient descent iterates with dropout in the linear regression model. In particular, non-asymptotic bounds for expectations and covariance matrices of the iterates are derived. In contrast with the widely cited connection between dropout and $\ell_2$-regularization in expectation, the results indicate a much more subtle relationship, owing to interactions between the gradient descent dynamics and the additional randomness induced by dropout. We also study a simplified variant of dropout which does not have a regularizing effect and converges to the least squares estimator.

Spike and slab variational Bayes for high dimensional logistic regression

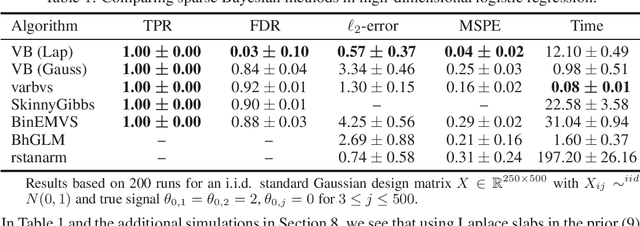
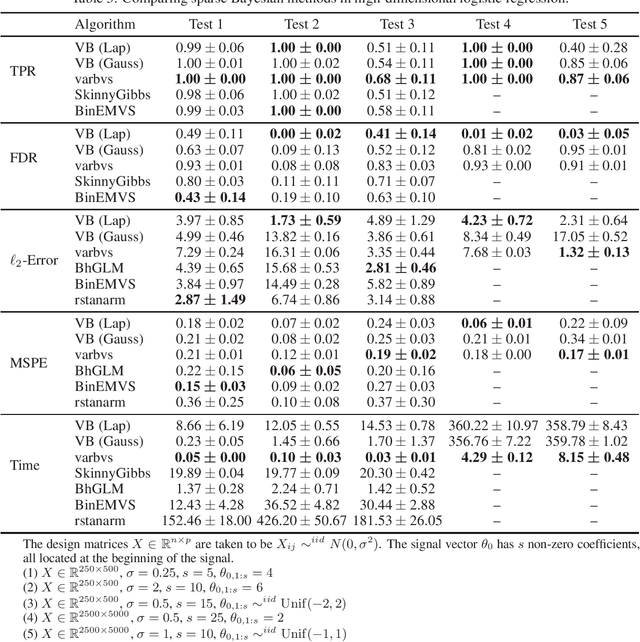
Variational Bayes (VB) is a popular scalable alternative to Markov chain Monte Carlo for Bayesian inference. We study a mean-field spike and slab VB approximation of widely used Bayesian model selection priors in sparse high-dimensional logistic regression. We provide non-asymptotic theoretical guarantees for the VB posterior in both $\ell_2$ and prediction loss for a sparse truth, giving optimal (minimax) convergence rates. Since the VB algorithm does not depend on the unknown truth to achieve optimality, our results shed light on effective prior choices. We confirm the improved performance of our VB algorithm over common sparse VB approaches in a numerical study.