Contraction rates for conjugate gradient and Lanczos approximate posteriors in Gaussian process regression

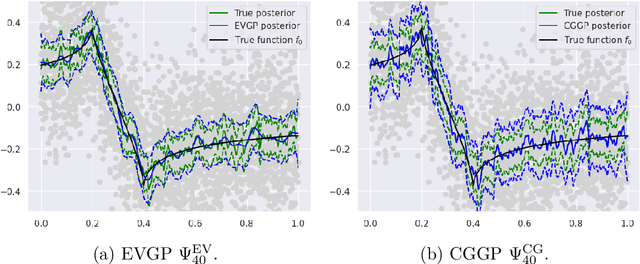
Due to their flexibility and theoretical tractability Gaussian process (GP) regression models have become a central topic in modern statistics and machine learning. While the true posterior in these models is given explicitly, numerical evaluations depend on the inversion of the augmented kernel matrix $ K + \sigma^2 I $, which requires up to $ O(n^3) $ operations. For large sample sizes n, which are typically given in modern applications, this is computationally infeasible and necessitates the use of an approximate version of the posterior. Although such methods are widely used in practice, they typically have very limtied theoretical underpinning. In this context, we analyze a class of recently proposed approximation algorithms from the field of Probabilistic numerics. They can be interpreted in terms of Lanczos approximate eigenvectors of the kernel matrix or a conjugate gradient approximation of the posterior mean, which are particularly advantageous in truly large scale applications, as they are fundamentally only based on matrix vector multiplications amenable to the GPU acceleration of modern software frameworks. We combine result from the numerical analysis literature with state of the art concentration results for spectra of kernel matrices to obtain minimax contraction rates. Our theoretical findings are illustrated by numerical experiments.

Variational Gaussian Processes For Linear Inverse Problems

By now Bayesian methods are routinely used in practice for solving inverse problems. In inverse problems the parameter or signal of interest is observed only indirectly, as an image of a given map, and the observations are typically further corrupted with noise. Bayes offers a natural way to regularize these problems via the prior distribution and provides a probabilistic solution, quantifying the remaining uncertainty in the problem. However, the computational costs of standard, sampling based Bayesian approaches can be overly large in such complex models. Therefore, in practice variational Bayes is becoming increasingly popular. Nevertheless, the theoretical understanding of these methods is still relatively limited, especially in context of inverse problems. In our analysis we investigate variational Bayesian methods for Gaussian process priors to solve linear inverse problems. We consider both mildly and severely ill-posed inverse problems and work with the popular inducing variables variational Bayes approach proposed by Titsias in 2009. We derive posterior contraction rates for the variational posterior in general settings and show that the minimax estimation rate can be attained by correctly tunned procedures. As specific examples we consider a collection of inverse problems including the heat equation, Volterra operator and Radon transform and inducing variable methods based on population and empirical spectral features.

Analyzing hierarchical multi-view MRI data with StaPLR: An application to Alzheimer's disease classification

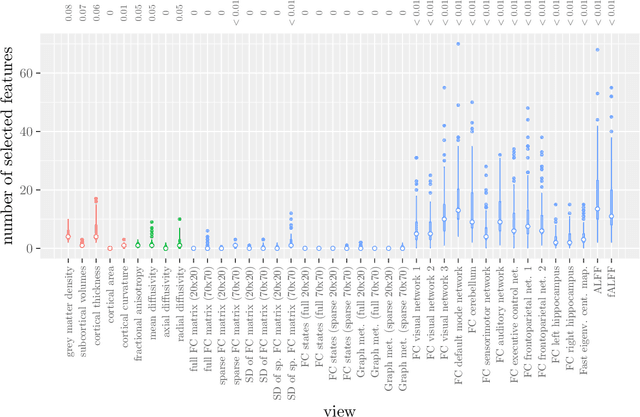
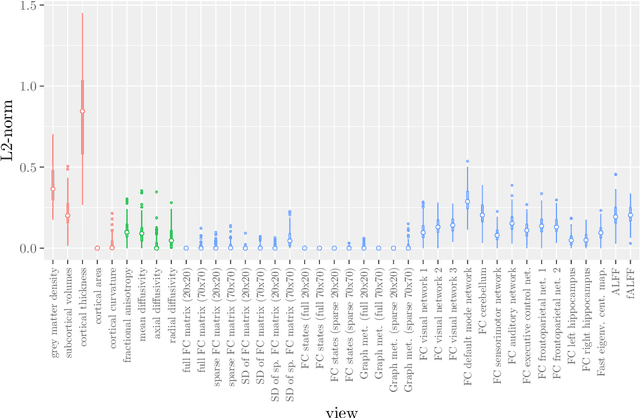
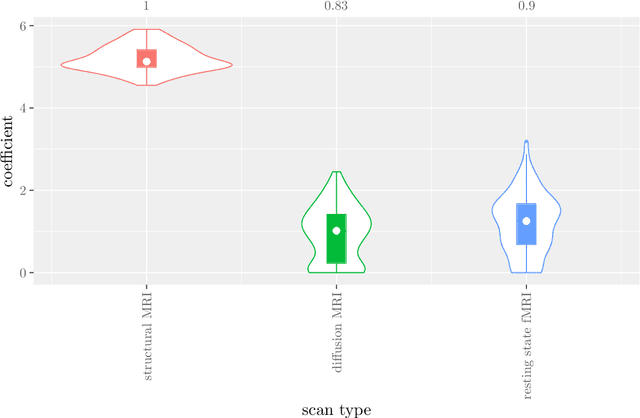
Multi-view data refers to a setting where features are divided into feature sets, for example because they correspond to different sources. Stacked penalized logistic regression (StaPLR) is a recently introduced method that can be used for classification and automatically selecting the views that are most important for prediction. We show how this method can easily be extended to a setting where the data has a hierarchical multi-view structure. We apply StaPLR to Alzheimer's disease classification where different MRI measures have been calculated from three scan types: structural MRI, diffusion-weighted MRI, and resting-state fMRI. StaPLR can identify which scan types and which MRI measures are most important for classification, and it outperforms elastic net regression in classification performance.

Optimal distributed testing in high-dimensional Gaussian models

In this paper study the problem of signal detection in Gaussian noise in a distributed setting. We derive a lower bound on the size that the signal needs to have in order to be detectable. Moreover, we exhibit optimal distributed testing strategies that attain the lower bound.

View selection in multi-view stacking: Choosing the meta-learner

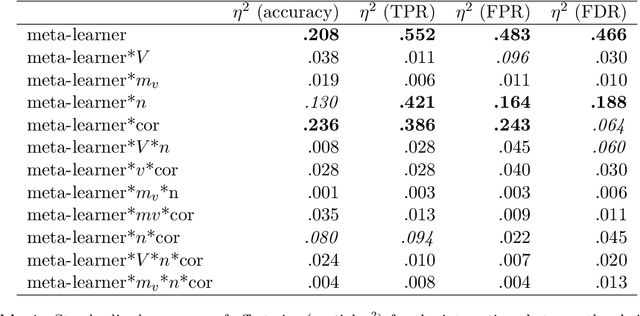
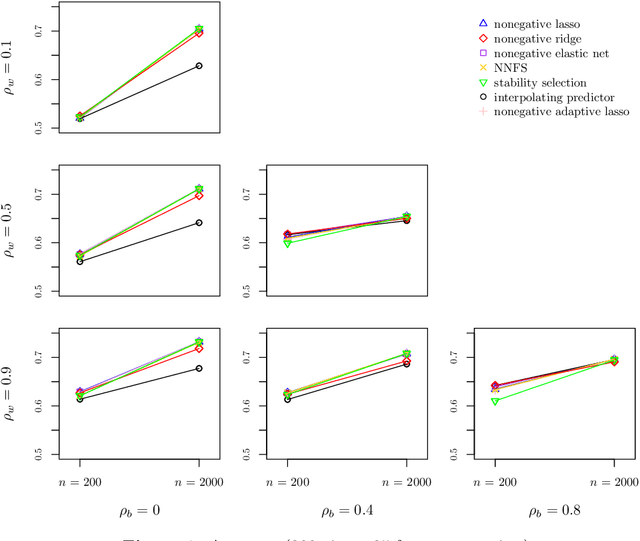
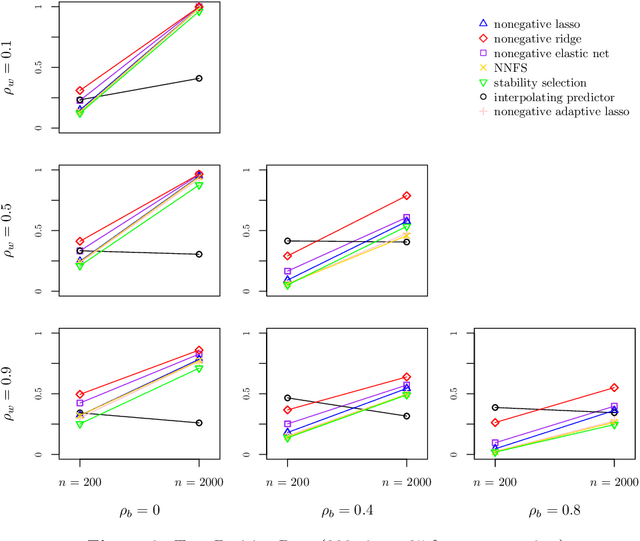
Multi-view stacking is a framework for combining information from different views (i.e. different feature sets) describing the same set of objects. In this framework, a base-learner algorithm is trained on each view separately, and their predictions are then combined by a meta-learner algorithm. In a previous study, stacked penalized logistic regression, a special case of multi-view stacking, has been shown to be useful in identifying which views are most important for prediction. In this article we expand this research by considering seven different algorithms to use as the meta-learner, and evaluating their view selection and classification performance in simulations and two applications on real gene-expression data sets. Our results suggest that if both view selection and classification accuracy are important to the research at hand, then the nonnegative lasso, nonnegative adaptive lasso and nonnegative elastic net are suitable meta-learners. Exactly which among these three is to be preferred depends on the research context. The remaining four meta-learners, namely nonnegative ridge regression, nonnegative forward selection, stability selection and the interpolating predictor, show little advantages in order to be preferred over the other three.

Spike and slab variational Bayes for high dimensional logistic regression

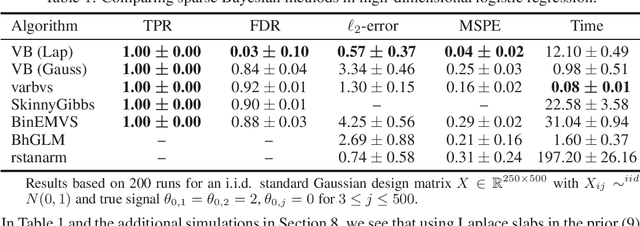
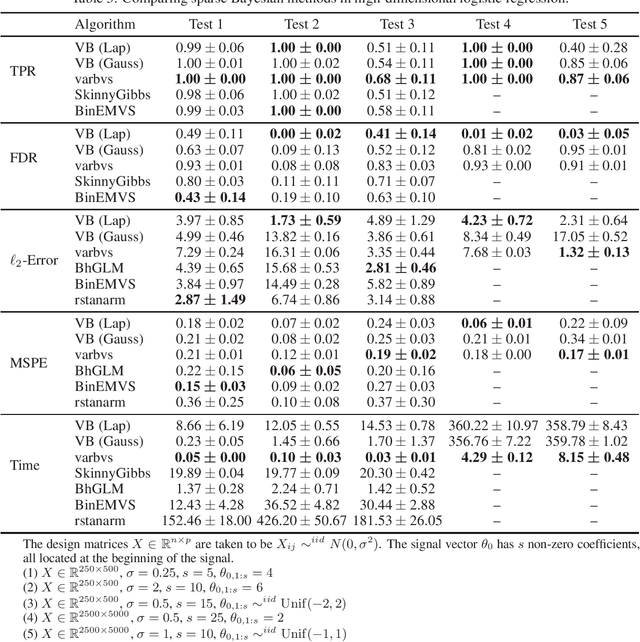
Variational Bayes (VB) is a popular scalable alternative to Markov chain Monte Carlo for Bayesian inference. We study a mean-field spike and slab VB approximation of widely used Bayesian model selection priors in sparse high-dimensional logistic regression. We provide non-asymptotic theoretical guarantees for the VB posterior in both $\ell_2$ and prediction loss for a sparse truth, giving optimal (minimax) convergence rates. Since the VB algorithm does not depend on the unknown truth to achieve optimality, our results shed light on effective prior choices. We confirm the improved performance of our VB algorithm over common sparse VB approaches in a numerical study.

Distributed function estimation: adaptation using minimal communication

We investigate whether in a distributed setting, adaptive estimation of a smooth function at the optimal rate is possible under minimal communication. It turns out that the answer depends on the risk considered and on the number of servers over which the procedure is distributed. We show that for the $L_\infty$-risk, adaptively obtaining optimal rates under minimal communication is not possible. For the $L_2$-risk, it is possible over a range of regularities that depends on the relation between the number of local servers and the total sample size.

Debiased Bayesian inference for average treatment effects

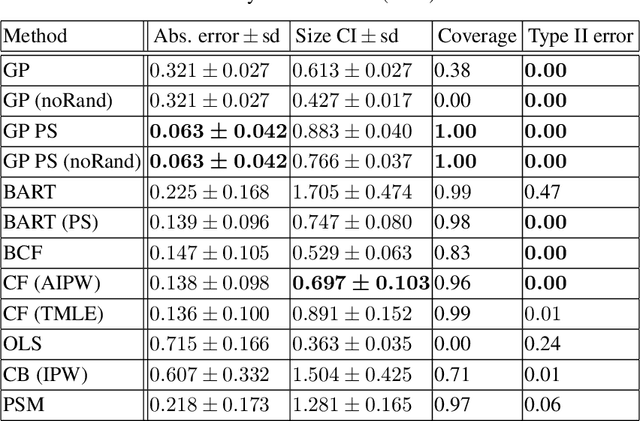
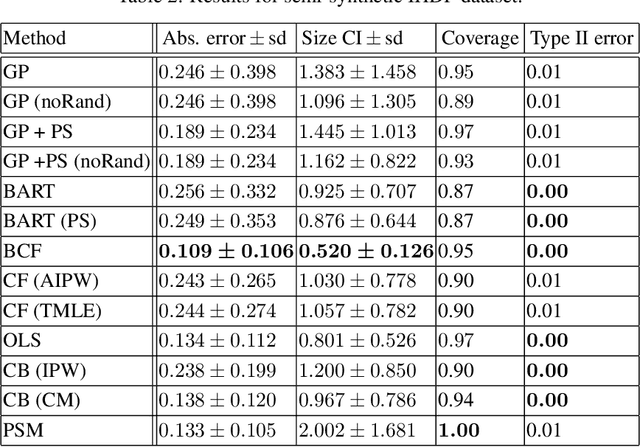
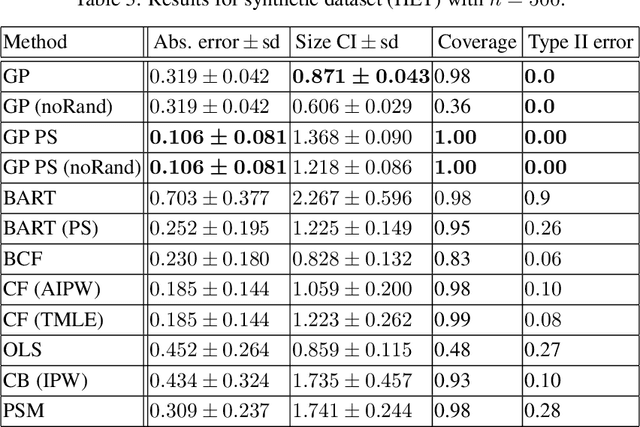
Bayesian approaches have become increasingly popular in causal inference problems due to their conceptual simplicity, excellent performance and in-built uncertainty quantification ('posterior credible sets'). We investigate Bayesian inference for average treatment effects from observational data, which is a challenging problem due to the missing counterfactuals and selection bias. Working in the standard potential outcomes framework, we propose a data-driven modification to an arbitrary (nonparametric) prior based on the propensity score that corrects for the first-order posterior bias, thereby improving performance. We illustrate our method for Gaussian process (GP) priors using (semi-)synthetic data. Our experiments demonstrate significant improvement in both estimation accuracy and uncertainty quantification compared to the unmodified GP, rendering our approach highly competitive with the state-of-the-art.

Stacked Penalized Logistic Regression for Selecting Views in Multi-View Learning

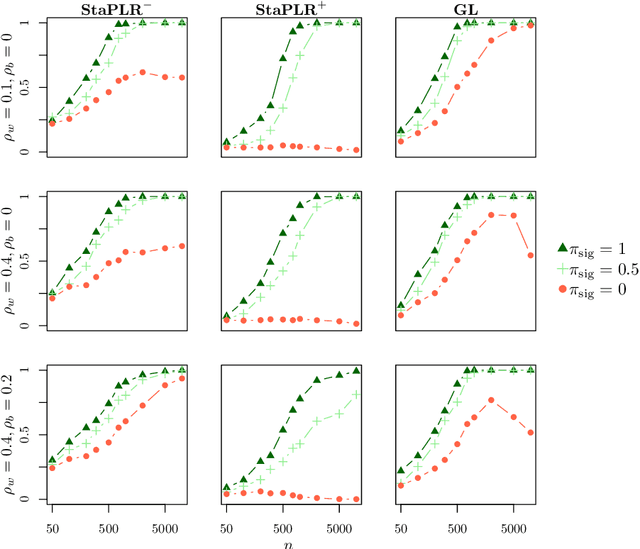
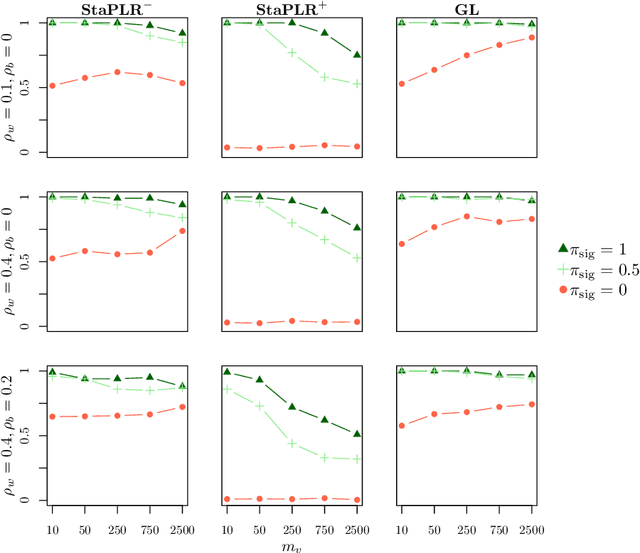
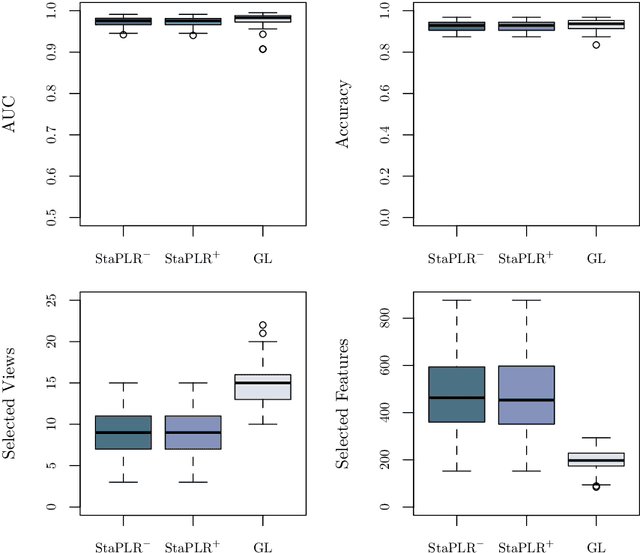
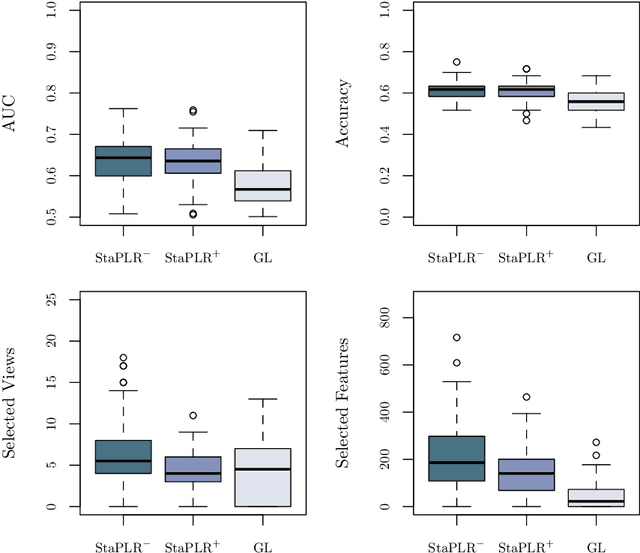
In multi-view learning, features are organized into multiple sets called views. Multi-view stacking (MVS) is an ensemble learning framework which learns a prediction function from each view separately, and then learns a meta-function which optimally combines the view-specific predictions. In case studies, MVS has been shown to increase prediction accuracy. However, the framework can also be used for selecting a subset of important views. We propose a method for selecting views based on MVS, which we call stacked penalized logistic regression (StaPLR). Compared to existing view-selection methods like the group lasso, StaPLR can make use of faster optimization algorithms and is easily parallelized. We show that nonnegativity constraints on the parameters of the function which combines the views are important for preventing unimportant views from entering the model. We investigate the view selection and classification performance of StaPLR and the group lasso through simulations, and consider two real data examples. We observe that StaPLR is less likely to select irrelevant views, leading to models that are sparser at the view level, but which have comparable or increased predictive performance.

Adaptive distributed methods under communication constraints

We study distributed estimation methods under communication constraints in a distributed version of the nonparametric signal-in-white-noise model. We derive minimax lower bounds and exhibit methods that attain those bounds. Moreover, we show that adaptive estimation is possible in this setting.